Навигация
Анализ равновесных данных
4.2. Анализ равновесных данных
Полученные значения констант равновесия анализировались с помощью подхода, основанного на последовательном исключении из исходной жидкофазной константы равновесия вкладов, обусловленных:
· межмолекулярными взаимодействиями,
· симметрией внешнего вращения молекул,
· вращением молекулы как целого,
· смешением конформеров,
· колебательным движением,
· вращением отдельных групп в молекулах реагентов.
Результатом подобного исключения является переход к газофазной константе равновесия ![]() , рассчитываемой следующим образом:
, рассчитываемой следующим образом:
![]() = exp(ln Kps - DS(or)/R - DS(mix)/R - DS(vib)/R - DS(ir)/R),
= exp(ln Kps - DS(or)/R - DS(mix)/R - DS(vib)/R - DS(ir)/R),
где ![]() - бессимметрийная газофазная константа равновесия реакции, DS(or) = SoII,g,(or) - SoI,g,(or); DS(mix) = SoII,g,(mix) - SoI,g,(mix); DS(vib) = SoII,g,(vib) - SoI,g,(vib); DS(ir) = SoII,g,(ir) - SoI,g,(ir).– соответственно, энтропийные вклады, обусловленные вращением молекулы как целого, смешением конформеров, колебательным движением и заторможенным вращением групп в молекуле, рассчитываемые как разность соответствующих энтропийных составляющих конечных (II) и исходных веществ (I).
- бессимметрийная газофазная константа равновесия реакции, DS(or) = SoII,g,(or) - SoI,g,(or); DS(mix) = SoII,g,(mix) - SoI,g,(mix); DS(vib) = SoII,g,(vib) - SoI,g,(vib); DS(ir) = SoII,g,(ir) - SoI,g,(ir).– соответственно, энтропийные вклады, обусловленные вращением молекулы как целого, смешением конформеров, колебательным движением и заторможенным вращением групп в молекуле, рассчитываемые как разность соответствующих энтропийных составляющих конечных (II) и исходных веществ (I).
Анализ констант равновесия проводился следующим образом.
Путем исключения вклада на симметрию молекул находилась бессимметрийная жидкофазная константа реакции  , здесь числа симметрии s
формируются на основании как симметрии наружного вращения молекулы, так и симметрии внутреннего вращения тех групп, симметрия которых не может быть учтена при анализе энтропийного вклада, обусловленного внутренним вращением. Для систем, рассмотренных в данной работе, такими группами были фениленовые фрагменты.
, здесь числа симметрии s
формируются на основании как симметрии наружного вращения молекулы, так и симметрии внутреннего вращения тех групп, симметрия которых не может быть учтена при анализе энтропийного вклада, обусловленного внутренним вращением. Для систем, рассмотренных в данной работе, такими группами были фениленовые фрагменты.
Путем снятия вклада на межмолекулярные взаимодействия рассчитывалась бессимметрийная газофазная константа равновесия реакции 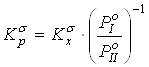 . Давления насыщенного пара
. Давления насыщенного пара ![]() рассчитывались методом Ли-Кеслера [50] или по экспериментальным данным. Применение к расчету давлений насыщенного пара методики, описанной в главе 2.1, позволяет обеспечить погрешность расчета не более 10% отн. для всех давлений, приведенных в данной работе. Вопросы расчета критических температур и давлений (Tc и Pc) изложены в главе 2, ацентрические факторы (w) рассчитывались по уравнению Ли-Кеслера [50].
рассчитывались методом Ли-Кеслера [50] или по экспериментальным данным. Применение к расчету давлений насыщенного пара методики, описанной в главе 2.1, позволяет обеспечить погрешность расчета не более 10% отн. для всех давлений, приведенных в данной работе. Вопросы расчета критических температур и давлений (Tc и Pc) изложены в главе 2, ацентрические факторы (w) рассчитывались по уравнению Ли-Кеслера [50].
Остальные вклады требовали привлечения информации о геометрии, энергетических характеристиках молекул и частотах колебательного спектра. Для получения подобной информации нами использовались различные расчетные методы. Окончательная обработка информации и вычисление энтропийных вкладов выполнялась с помощью программы Entropy, описание которой будет приведено в п. 4.3.
Геометрия молекулы оптимизировалась методом молекулярной механики (силовое поле MMX на базе силового поля Аллинджера MM2) программой PCModel 3.2. Для оптимизации молекул бифенилов использовалась PCModel 4.0, обладающая большими возможностями при расчетах в p-электронных системах. Выходной информацией являлись оптимизированная геометрия молекулы для наиболее устойчивого конформера и информация об изменении энергии молекулы при вращении каждого из волчков, сохраняемые в отдельных файлах. Для формирования потенциальной кривой барьера вращения каждого из волчков использовались значения потенциальной энергии молекулы при изменении двугранного угла между избранными связями волчка и остова от 0о до 360о с шагом 10о, при этом на каждом фиксированном значении угла проводилась оптимизация геометрии молекулы.
На основании сведений о геометрии молекулы рассчитывалось произведение главных центральных моментов инерции IAIBIC , являющееся свободным членом кубического уравнения
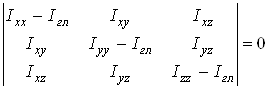 ,
,
где 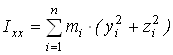 ,
, 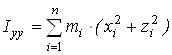 ,
, 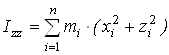 ,
, 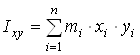 ,
, 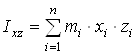 ,
, 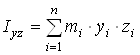 - моменты инерции молекулы (здесь n – число атомов в молекуле; mi – масса i-го атома; xi, yi, zi – координаты i-го атома в системе координат с центром, находящемся в центре инерции молекулы). Отсюда
- моменты инерции молекулы (здесь n – число атомов в молекуле; mi – масса i-го атома; xi, yi, zi – координаты i-го атома в системе координат с центром, находящемся в центре инерции молекулы). Отсюда
![]()
В дальнейшем рассчитывалась сумма состояний жесткого ротатора

и вклад в энтропию, обусловленный вращением молекулы как целого
![]()
где s – число симметрии молекулы, h – постоянная Планка, k – постоянная Больцмана.
На основании полученных ранее сведений об изменении энергии молекулы при вращении каждой из ее групп рассчитывался вклад в энтропию от смешения конформеров
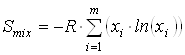
где m – общее количество конформеров (в нашем случае учитывались все состояния, полученные при повороте волчка от 0о до 350о с шагом 10о, то есть m=36∙n, где n – число вращающихся групп в молекуле), xi – мольная доля каждой конформации

где n – число вращающихся групп в молекуле, m – количество конформеров, Ei – энергия молекулы в данном состоянии равная ![]() , где
, где ![]() - исходное значение энергии,
- исходное значение энергии, ![]() - наименьшая энергия молекулы, полученная при вращении всех возможных волчков.
- наименьшая энергия молекулы, полученная при вращении всех возможных волчков.
Для нахождения вклада в энтропию, обусловленного колебательным движением были использованы расчетные значения частот колебательного спектра, полученные полуэмпирическим методом PM3 (HyperChem 5.0) для оптимизированной тем же методом геометрии молекулы. Критерием качества оптимизации служило отсутствие в спектре отрицательных значений частот.
Расчет вклада в энтропию, обусловленного колебательным движением производился следующим образом.
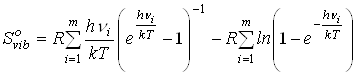
где νi – частота из принятого к расчету набора, m – количество частот в наборе. Из полного набора частот колебательного спектра исключены крутильные колебания, соответствующие вращению групп, участвующих в расчете вклада в энтропию от заторможенного вращения, таким образом ![]() , где n – число атомов в молекуле, ntop – число волчков. При отсутствии надежных методик определения крутильных колебаний в спектре нами применялась приближенная оценка типов колебаний с использованием режима Animate программы HyperChem 5.0.
, где n – число атомов в молекуле, ntop – число волчков. При отсутствии надежных методик определения крутильных колебаний в спектре нами применялась приближенная оценка типов колебаний с использованием режима Animate программы HyperChem 5.0.
Информация о геометрии молекулы и потенциальных кривых барьеров вращения волчков использовалась для расчета вклада в энтропию, обусловленного внутренним вращением групп в молекуле. Энтропийный вклад определялся как
![]()
здесь n – число максимумов потенциальной кривой барьера вращения группы, s– число симметрии группы (подходы к определению чисел симметрии вращающихся групп были рассмотрены в главе 1), Sfr – энтропия свободного вращения волчка, ![]() - разность между энтропиями свободного и заторможенного вращения, определяемая по таблицам Питцера и Гуинна [21] как функция
- разность между энтропиями свободного и заторможенного вращения, определяемая по таблицам Питцера и Гуинна [21] как функция ![]() и
и ![]() , где Vo – эффективный барьер вращения волчка, Qfr – статистическая сумма по состояниям свободного внутреннего вращения.
, где Vo – эффективный барьер вращения волчка, Qfr – статистическая сумма по состояниям свободного внутреннего вращения.
Величина эффективного барьера вращения принималась равной 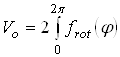 , где
, где ![]() - зависимость изменения потенциальной энергии молекулы от угла поворота волчка φ. Для расчета Vo полученные методом молекулярной механики значения потенциальной энергии молекулы при заданных значениях угла поворота волчка описывались с помощью кубического сплайна, затем полученный сплайн интегрировался по методу Симпсона.
- зависимость изменения потенциальной энергии молекулы от угла поворота волчка φ. Для расчета Vo полученные методом молекулярной механики значения потенциальной энергии молекулы при заданных значениях угла поворота волчка описывались с помощью кубического сплайна, затем полученный сплайн интегрировался по методу Симпсона.
Статистическая сумма по состояниям свободного внутреннего вращения рассчитывалась как 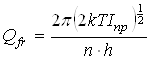 , где Iпр – приведенный момент инерции волчка, который рассчитывался в соответствии со следующей процедурой [105].
, где Iпр – приведенный момент инерции волчка, который рассчитывался в соответствии со следующей процедурой [105].
Для вращающейся группы вводится координатная система с осями x, y, z, расположенными следующим образом: ось z совпадает с осью вращения волчка, ось x проходит через центр масс волчка и перпендикулярна оси z, ось y проходит через точку пересечения осей x, z и перпендикулярна к ним. Атомы волчка, лежащие на оси z из дальнейшего рассмотрения исключаются. Далее производится расчет следующих величин: ![]() - момент инерции волчка относительно оси z,
- момент инерции волчка относительно оси z, ![]() и
и ![]() - произведения моментов инерции,
- произведения моментов инерции, ![]() - фактор несбалансированности волчка.
- фактор несбалансированности волчка.
Затем находятся направляющие косинусы осей x, y, z относительно главных центральных осей 1, 2, 3 инерции молекулы. Направление осей выбирается таким образом, чтобы обе системы координат были или правыми или левыми. При этом должно соблюдаться условие равенства единице определителя матрицы направляющих косинусов, то есть

что может использоваться для проверки правильности определения направляющих косинусов.
Приведенный момент инерции рассчитывается следующим образом:
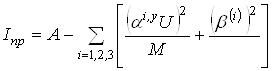
где ![]() . Здесь r(i) – проекции на главные оси инерции молекулы вектора, направленного из центра тяжести молекулы в центр координат волчка, индекс i принимает значения 1, 2, 3 в циклическом порядке, то есть при i=1 индекс i-1 равен 3, а индекс i+1 при i=3 равен 1.
. Здесь r(i) – проекции на главные оси инерции молекулы вектора, направленного из центра тяжести молекулы в центр координат волчка, индекс i принимает значения 1, 2, 3 в циклическом порядке, то есть при i=1 индекс i-1 равен 3, а индекс i+1 при i=3 равен 1.
В ходе анализа для изучения влияния каждого из энтропийных вкладов на константу равновесия рассматривался следующий ряд величин, получаемых при последовательном исключении из исходной константы равновесия Kx каждого из обозначенных ранее энтропийных вкладов:
1. Бессимметрийная константа равновесия в жидкой фазе - 
2. Бессимметрийная константа равновесия в газовой фазе - 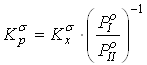
3. ![]() с исключенным вкладом на вращение молекулы как целого -
с исключенным вкладом на вращение молекулы как целого - ![]()
4. “Существенная” газофазная константа равновесия, полученная после исключения из ![]() вклада на смешение конформеров -
вклада на смешение конформеров - ![]()
5. ![]() с исключенным вкладом от колебательного движения -
с исключенным вкладом от колебательного движения - ![]()
6. ![]() после исключения вклада на внутреннее вращение -
после исключения вклада на внутреннее вращение - ![]()
Значения энтропийных вкладов и констант равновесия для изученных превращений приводится в табл. 5.1.
Одной из целей данной работы является совершенствование подхода к прогнозированию химического равновесия в реакциях позиционной изомеризации алкилароматических углеводородов и их функциональных производных. При прогнозировании констант равновесия с использованием уравнения
![]() (4.1)
(4.1)
необходима как можно более достоверная информация об энтальпии и изменении энтропии реакции. При этом экспериментальные данные по указанным свойствам не охватывают весь набор веществ, представляющих практический и теоретический интерес. Таким образом, при прогнозировании приходится прибегать к расчетным методам.
Расчет энтальпии реакции, как правило, производится при помощи аддитивных методов с учетом эффектов взаимодействия заместителей, полученных на основе экспериментальных калориметрических данных.
Использование аддитивных методов при прогнозировании энтропии веществ более проблематично по причине особой природы этого свойства, несмотря на то, что такие методы развиты и применяются при массовых расчетах термодинамических свойств органических веществ [50, 111]. Лучшим, на наш взгляд, подходом является расчет изменения энтропии реакций в соответствии с методами статистической термодинамики [21, 105, 106, 112], где свойство представляется в виде суммы вкладов различных видов движения молекул:
![]() . (4.2)
. (4.2)
В связи с тем, что в данной работе рассматриваются реакции позиционной изомеризации, вклад поступательного движения молекул (![]() ) и вклад электронных состояний молекул (
) и вклад электронных состояний молекул (![]() ) принимаются равными нулю вследствие равенства значений соответствующих составляющих энтропии у изомерных молекул. Методики расчета остальных составляющих энтропии описаны ранее в данном разделе.
) принимаются равными нулю вследствие равенства значений соответствующих составляющих энтропии у изомерных молекул. Методики расчета остальных составляющих энтропии описаны ранее в данном разделе.
В заключение следует остановиться еще на одном вопросе.
Очевидным является факт существования температурных зависимостей у вкладов, обусловленных смешением конформеров, колебательным движением и внутренним вращением, причем вид и параметры этих зависимостей определяются структурой молекул. Таким образом, при проведении анализа исключение указанных энтропийных вкладов приводит к изменению энтальпийного эффекта реакции при переходе от ![]() к
к ![]() . То есть, в общем случае, формирование дополнительной энтальпийной шкалы [12, 144] с самостоятельным набором эффектов взаимодействия заместителей в молекуле представляется вполне обоснованным.
. То есть, в общем случае, формирование дополнительной энтальпийной шкалы [12, 144] с самостоятельным набором эффектов взаимодействия заместителей в молекуле представляется вполне обоснованным.
Эти эффекты должны корректно описывать равновесие превращений при условии, что для последних выполняется условие ![]() =0.
=0.
Источником значений подобных эффектов служит эксперимент по химическому равновесию. Значения этих эффектов являются зависимыми от набора методов, с помощью которых рассчитываются энтропийные вклады в константу равновесия, особенно вклады, обусловленные внутренним вращением групп в молекулах и смешением конформеров. Поэтому результативным при прогнозировании может быть только совместное использование указанных энтальпийных эффектов и всей совокупности рекомендуемых расчетных методов.
Учитывая то, что для позиционных изомеров в сравнительно узком (100-150 К) температурном интервале изменения ![]() с температурой невелико [21], следует ожидать небольших изменений с температурой отдельных вкладов и энтальпийных эффектов при переходе от
с температурой невелико [21], следует ожидать небольших изменений с температурой отдельных вкладов и энтальпийных эффектов при переходе от ![]() к
к ![]() . Это в идеале предполагает отсутствие необходимости формирования дополнительной шкалы для эффектов взаимодействия заместителей в молекуле.
. Это в идеале предполагает отсутствие необходимости формирования дополнительной шкалы для эффектов взаимодействия заместителей в молекуле.
Похожие работы
... называется группа упорядоченных по величине значений признака, заменяемая в процессе расчетов средним значением. 2. Методы вторичной статистической обработки результатов эксперимента С помощью вторичных методов статистической обработки экспериментальных данных непосредственно проверяются, доказываются или опровергаются гипотезы, связанные с экспериментом. Эти методы, как правило, сложнее, ...
... В.Ю. Геометрическое представление данных психологических исследований. – М.: Наука. – 1990. 8. Лакин Г.Ф. Биометрия. – М.: Высшая школа. – 1973. – 343 с. 9. Лбов Г.С. Методы обработки разнотипных данных. – М.: Наука. – 1981. 10. Математические методы в исследованиях индивидуальной и групповой деятельности п/ред. Крылова В.Ю. – М.: Наука. – 1990. 11. Мацкевич И.П., ...
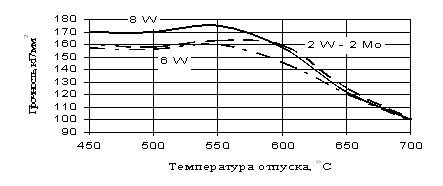
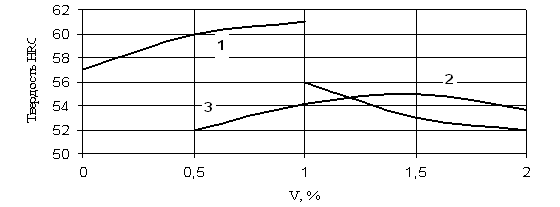
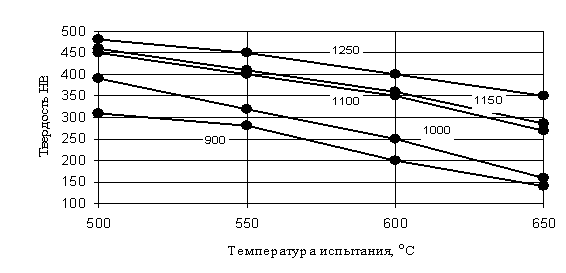
... отпуска может быть на 10–20оС ниже, а его продолжительность на 20–25% меньше, чем первого отпуска. Охлаждение после отпуска проводится на воздухе. 1.1.5 Влияние термической обработки на свойства штамповых сталей Служебные свойства штампового инструмента и его стойкость в значительной степени определяются соответствующим назначением марки стали, ее термообработкой и условиями эксплуатации ...
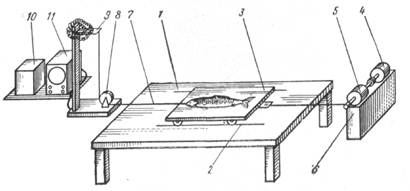
... силы взаимодействия между рыбой и рабочими органами машин, поскольку изменяется площадь контакта, обусловливающая силы трения. До настоящего времени структурно-механические характеристики в основном оцениваются органолептическим методом. Рыбу сдавливают пальцами и оценивают ее консистенцию. Не достатком такого метода оценки структурно-механических характеристик мышечной ткани является его ...
0 комментариев