КОНТРОЛЬНАЯ РАБОТА № 2
ВАРИАНТ 2.3
№ 1. Записать общее уравнение прямой, переходящей через точку М (-2, 4) перпендикулярно прямой x+2y+5=0. Найти площадь треугольника, образованного данной прямой с осями координат.
Запишем уравнение прямой в виде:
![]() .
.
Коэффициент К найдем из условия перпендикулярности прямых:
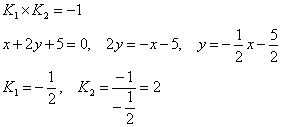
Получим уравнение прямой:
![]()
Сделаем чертеж
|
|
|
| Ответ: |
№ 2. Записать общее уравнение прямой, проходящей точку М (-2, 2) и отсекающей от первого координатного угла треугольник площадью S= 4,5 кв.ед.
Сделаем схематический чертеж
Площадь треугольника будет равна ![]() .
.
Координаты точек А и В найдем из уравнения прямой, которое запишем в виде

Из уравнения
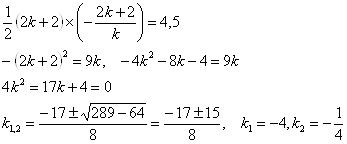
Получим прямую с угловым коэффициентом ![]()

Значение ![]() соответствует прямой, которая отсекает треугольник площадью S=4,5 от третьего координатного угла..
соответствует прямой, которая отсекает треугольник площадью S=4,5 от третьего координатного угла..
![]()
№ 3. Даны вершины треугольника А (2,1,0), В (3,-1,1) и С (1,2,-4). Записать общее уравнение плоскости, проходящей через сторону АВ перпендикулярно плоскости треугольника АВС.
Общее уравнение имеет вид:
![]()
Для нахождения A,B,C и D необходимо составить три уравнения.
Два уравнения получим из условия, что искомая плоскость проходит через точки А и В. Третье — из условия, что искомая плоскость перпендикулярна плоскости, проходящей через три точки А, В и С. условие перпендикулярности плоскостей:
![]()
Найдем уравнение плоскости, проходящей через точки А, В, С по формуле:
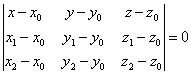
Разложим определитель по первой строке, подготовив числовые значения:
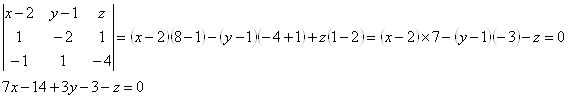
Получим уравнение плоскости:
![]()
Запишем условие перпендикулярности плоскостей:
![]()
Условие, что искомая плоскость:
через точку А: ![]() ;
;
через точку В: ![]() .
.
Получим систему уравнений:
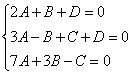
Складываем 2-е и 3-е уравнения: ![]() , 1-е уравнение умножаем на 2 и вычитаем из полученного:
, 1-е уравнение умножаем на 2 и вычитаем из полученного:
![]()
Из 1-го уравнения: ![]() .
.
Из 3-го уравнения: ![]() . Принимаем
. Принимаем ![]() , получаем
, получаем
![]() .
.
Уравнение плоскости имеет вид:
![]()
№ 4. Найти расстояние от точки ![]() до прямой
до прямой ![]() .
.
Расстояние r найдем по формуле расстояния от точки ![]() до прямой, заданной уравнением в канонической форме:
до прямой, заданной уравнением в канонической форме:
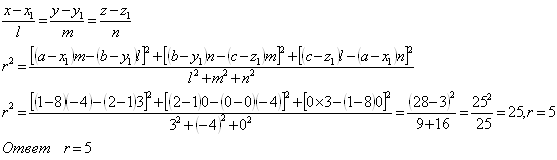
№ 5. Найти длину отрезка, отсекаемого от оси ординат плоскостью, которая проходит через точку ![]() перпендикулярно вектору
перпендикулярно вектору ![]() , где В — точка пересечения медиан треугольника, вершины которого совпадают с точками пересечения осей координат с плоскостью
, где В — точка пересечения медиан треугольника, вершины которого совпадают с точками пересечения осей координат с плоскостью
![]()
Для нахождения решения найдем уравнение плоскости, которая проходит через точку А в заданном направлении и подставим в это уравнение значение ![]() .
.
Для этого вначале найдем координаты точки В.
Точку пересечения заданной плоскости с осью ОХ найдем из уравнения:
![]()
с осью OY:
![]()
с осью OZ:
![]()
Получим треугольник с вершинами: ![]() .
.
Найдем координаты середины стороны ![]() по формуле:
по формуле:
![]() .
.
![]() — середина стороны
— середина стороны ![]() .
.
Теперь найдем точку В, используя свойство: медианы треугольника делятся в точке пересечения в отношении 2:1, считая от вершины. Используем формулу:
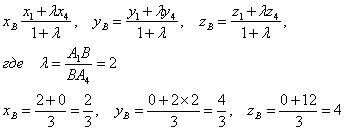
Точка пересечения медиан имеет координаты ![]() .
.
Найдем координаты вектора ![]() .
.
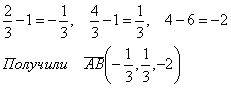
Уравнение искомой плоскости, проходящей через точку ![]() перпендикулярно вектору
перпендикулярно вектору ![]() имеет вид:
имеет вид:

№ 6. Две прямые параллельны плоскости ![]() . Первая прямая проходит через точку
. Первая прямая проходит через точку ![]() и пересекает ось абсцисс, вторая — через точку
и пересекает ось абсцисс, вторая — через точку ![]() и пересекает ось ординат. Найти косинус острого угла между направляющими векторами этих прямых.
и пересекает ось ординат. Найти косинус острого угла между направляющими векторами этих прямых.
Для нахождения направляющих векторов прямых используем условие параллельности прямой и плоскости
![]()
и условие, что прямая проходит через ось абсцисс, т.е. выполняется соотношение ![]() в точке (x,0,0).
в точке (x,0,0).
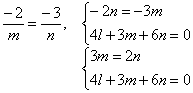
подставляем из 1-го уравнения во второе, получим
![]()
Полагаем ![]() тогда
тогда ![]() .
.
Получили направляющий вектор первой прямой (6,-2,-3).
Аналогично для второй прямой (она проходит через точку (0,y,0)
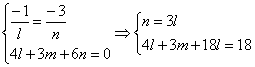
Из второго уравнения
![]()
Косинус найдем по формуле:
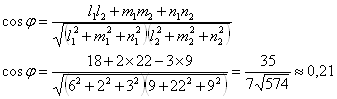
№ 7. Найти координаты центра ![]() окружности радиусом 5, касающейся прямой
окружности радиусом 5, касающейся прямой ![]() в точке М (2,0), если известно, что точка С расположена в первой четверти.
в точке М (2,0), если известно, что точка С расположена в первой четверти.
Переформулируем задачу:
Найти точку, лежащую на прямой, перпендикулярной прямой ![]() , проходящей через точку М (2,0) и отстоящую от нее на 5 ед.
, проходящей через точку М (2,0) и отстоящую от нее на 5 ед.
Запишем уравнение прямой в виде ![]() , коэффициент k найдем из условия перпендикулярности прямых
, коэффициент k найдем из условия перпендикулярности прямых
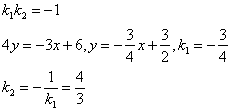
Получаем уравнение прямой
![]()
Используем формулу расстояния между двумя точками:
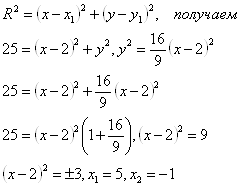
По условию второе решение не походит, т.к. x<0.
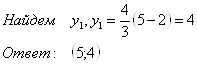
№ 8. Дана кривая ![]()
8.1. Доказать, что эта кривая — гипербола.
![]() — это каноническое уравнение гиперболы. Приведем исходное уравнение к этому виду
— это каноническое уравнение гиперболы. Приведем исходное уравнение к этому виду

Это каноническое уравнение гиперболы.
8.2 Найти координаты ее центра симметрии.
Сделаем схематический чертеж:
Центр симметрии гиперболы в точке ![]() .
.
![]() .
.
8.3. Найти действительную и мнимую полуоси.
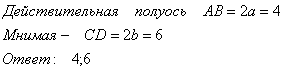
8.4. Записать уравнение фокальной оси.
Фокальная ось проходит через фокус ![]() , р-фокальный параметр (половина хорды, проведенной через фокус перпендикулярно действительной оси).
, р-фокальный параметр (половина хорды, проведенной через фокус перпендикулярно действительной оси).
Уравнение ![]() , где
, где
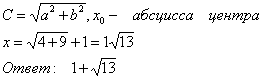
8.5. Построить данную гиперболу построение проведено в п.8.2.
№ 9. Дана кривая ![]() .
.
9.1. Доказать, что данная кривая — парабола.
Каноническое уравнение параболы ![]() , заданное уравнение приведем к этому виду
, заданное уравнение приведем к этому виду
![]()
следовательно, имеем параболу.
9.2. Найти координаты ее вершины.
Если уравнение параболы записано в виде ![]() , координаты вершины
, координаты вершины ![]() .
.
![]()
9.3. Найти значение ее параметра р.
Из уравнения—— видно, что ![]() .
.
![]()
9.4. Записать уравнение ее оси симметрии.
Данная ось проходит через вершину параболы перпендикулярно оси ОХ, ее уравнение ![]() .
.
![]()
9.5. Построить данную параболу.
Все параметры известны. Найдем пересечение с осью OY.
![]()
№ 10. Дана кривая ![]() .
.
10.1. Доказать, что эта кривая — эллипс.
Каноническое уравнение эллипса
![]()
Общее уравнение кривой второго порядка:
![]() .
.
Перепишем заданное уравнение:
![]()
Введем обозначения:
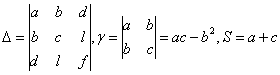
Если ![]() имеем эллипс. Проводим вычисления при a=8, b=6, c=17,d=-14, l=-23, f=-43.
имеем эллипс. Проводим вычисления при a=8, b=6, c=17,d=-14, l=-23, f=-43.

следовательно, исходная кривая — эллипс.
10.2. Найти координаты центра его симметрии.
Применим формулу:

10.3. Найти его большую и малую полуоси.
Для этого приведем уравнение к каноническому виду, вычислим:
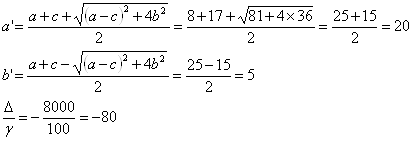
Уравнение запишем в виде:
![]() где
где
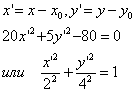
Получим уравнение эллипса в новых координатах, где осями координат являются оси, полученные переносом начала координат в центр эллипса ![]() и поворотом осей на угол α, определяемый уравнением
и поворотом осей на угол α, определяемый уравнением ![]() , при этом угловой коэффициент новой оси
, при этом угловой коэффициент новой оси ![]()
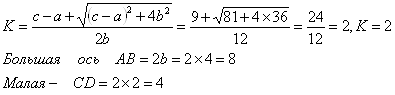
10.4. Записать общее уравнение фокальной оси.
Фокальная ось проходит через фокус перпендикулярно оси ![]() . В новых координатах
. В новых координатах ![]() .
.
Воспользуемся формулой преобразования координат:
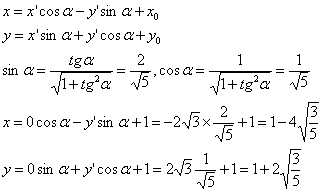
Осталось составить уравнение прямой, проходящей через точку с коэффициентом наклона 2. Общий вид такой прямой ![]() , получим:
, получим:
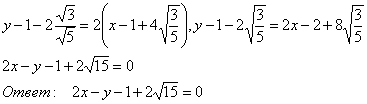
10.5. Построить данную кривую.
Для этого в старой системе координат строим новую систему. Новые оси направлены по прямым — y=2x-1 и ![]() . Далее, определим вершины эллипса.
. Далее, определим вершины эллипса.
В новых координатах они равны ![]() .
.
В старых:
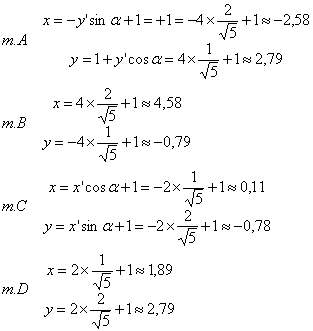
Похожие работы
... шаг интегрирования ; tp – время интегрирования трех точечным методом прогноза и коррекции , ta – время интегрирования по методу Адамса-Башфорта , NU – массив начальных условий . Данная процедура способна производить решения систем линейных дифференциальных уравнений произвольного размера , на произвольном промежутке времени интегрирования . Вычисленные данные записываются в файлы prandcom*.df . ...
... 6 3 = 26. Таким образом, для того, чтобы обеспечить минимум затрат (26 коп. в день), необходимо дневной рацион составить из 2 кг корма 1 и 3 кг корма 2. 2.2. Обобщение графического метода решения задач линейного программирования. Вообще, с помощью графического метода может быть ре-шена задача линейного программирования, система ограниче-ний которой содержит n неизвестных и m линейно ...
... решения останется неизменным, т.е. будет состоять из переменных (Х3,Х6,Х4,Х5). СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.1. – Мн.: БГУИР, 1995. 2. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного ...
... области (если допустимая область ограничена и не пуста); 3. ограниченность целевой функции в допустимой области является необходимым и достаточным условием разрешимости задачи. Гл 2 Решение задач линейного программирования графическим способом на ЭВМ 2.1 Описание работы программы Программа написана с использованием собственных функций и процедур и трех стандартных модулей System, Crt и ...
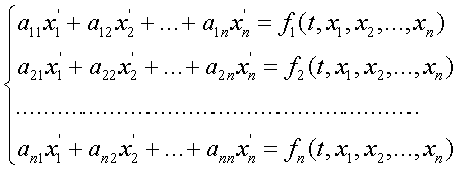
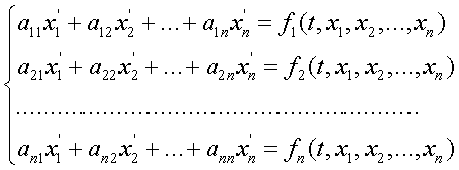
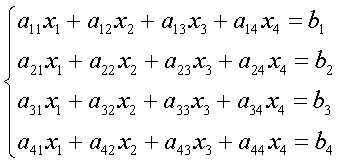




0 комментариев