Навигация
Использование определения логарифма
2. Использование определения логарифма
Пример 1. Решить уравнения
| a) log2(5 + 3log2(x - 3)) = 3, | c) log(x - 2)9 = 2, |
| b) | d) log2x + 1(2x2 - 8x + 15) = 2. |
Решение. a) Логарифмом положительного числа b по основанию a (a > 0, a ≠ 1) называется степень, в которую нужно возвести число a, чтобы получить b. Таким образом, logab = c, b = ac и, следовательно,
5 + 3log2(x - 3) = 23
или
3log2(x - 3) = 8 - 5, log2(x - 3) = 1.
Опять используя определение, получим
x - 3 = 21, x = 5.
Проверка полученного корня является неотъемлемой частью решения этого уравнения:
log2(5 + 3log2(5 - 3)) = log2(5 + 3log22) = log2(5 + 3) = log28 = 3.
Получим истинное равенство 3 = 3 и, следовательно, x = 5 есть решение исходного уравнения.
b) Аналогично примеру a), получим уравнение
![]()
откуда следует линейное уравнение x - 3 = 3(x + 3) с решением x = -6. Сделаем проверку и убедимся, что x = -6 является корнем исходного уравнения.
c) Аналогично примеру a), получим уравнение
(x - 2)2 = 9.
Возведя в квадрат, получим квадратное уравнение x2 - 4x - 5 = 0 с решениями x1 = -1 и x2 = 5. После проверки остается лишь x = 5.
d) Используя определение логарифма, получим уравнение
(2x2 - 8x + 15) = (2x + 1)2
или, после элементарных преобразований,
x2 + 6x-7 = 0,
откуда x1 = -7 и x2 = 1. После проверки остается x = 1.
3. Использование свойств логарифма
Пример 3. Решить уравнения
| a) log3x + log3(x + 3) = log3(x + 24), |
| b) log4(x2 - 4x + 1) - log4(x2 - 6x + 5) = -1/2 |
| c) log2x + log3x = 1 |
Решение. a) ОДЗ уравнения есть множество x (0;+) которое определяется из системы неравенств (условия существования логарифмов уравнения)
|
| x > 0, |
| x+3 > 0, | |
| x+24 > 0. |
Используя свойство P2 и утверждение 1, получим
|
| | |||||||||||||||
|
|
| x = 4. | ||||||||||||||
b) Используя свойство P3, получим следствие исходного уравнения
![]()
откуда, используя определение логарифма, получим
![]()
или
x2 - 4x + 1 = 1/2(x2 - 6x + 5),
откуда получаем уравнение
x2 - 2x - 3 = 0
с решениями x1 = -1 и x = 3. После проверки остается лишь x = -1.
c) ОДЗ уравнения: x (0;+). Используя свойство P5, получим уравнение
![]()
![]()
log2x(1 + log32) = 1,
откуда ![]() или
или ![]() или log2x = log63. Следовательно,
или log2x = log63. Следовательно, ![]()
Логарифмические неравенства
Неравенство, содержащее неизвестное под знаком логарифма или в его основании называется логарифмическим неравенством. В процессе решения логарифмических неравенств часто используются следующие утверждения относительно равносильности неравенств и учитываются свойства монотонности логарифмической функции.
Утверждение 1. Если a > 1, то неравенство loga f(x) > loga g(x) равносильно системе неравенств
|
| f(x) > g(x), |
| g(x) > 0. |
Утверждение 2. Если 0 < a < 1, то неравенство loga f(x) > loga g(x) равносильно системе неравенств
|
| f(x) < g(x), |
| f(x) > 0. |
Утверждение 3. Неравенство logh(x) f(x) > logh(x) g(x) равносильно совокупности систем неравенств
|
|
| h(x) > 1, |
| f(x) > g(x) > 0, | ||
|
| 0 < h(x) < 1, | |
| 0 < f(x) < g(x). |
Подчеркнем, что в неравенстве loga f(x) > loga g(x) вместо знака > может фигурировать любой из знаков ≥ , < , ≤ . В этом случае утверждения 1-3 соответственно преобразуются.
Пример 1. Решить неравенства
| a) log3(x2 - x) ≥ log3(x + 8); | |
| b) | |
| c) |
Решение. a) Используя утверждение 1 , получим
| log3(x2 - x) ≥ log3(x + 8) | x2 - x ≥ x + 8, | | x2 - 2x - 8 ≥ 0, | |
| x+8 > 0, | x > -8, |
| |
| x ≤ -2, | |
| x ≥ 4, | x | ||
| x > -8, |
b) Основание логарифма число между нулем и единицей, поэтому, используя утверждение 2, получим
|
|
|
|
|
|
|
|
c) Запишем 0 = log2
Похожие работы
... «нет» – Выписываете свой фигуры в одну строчку. В-1 В-2 , х = – 12 , х = 5 , х= – 22 , х = – 8 , х = – 11 , х = – 2 , х = 3 , х = – 4 Ответы: ^-^^ -^^- Итог урока: Сейчас мы сдадим мини экзамен по теме нашего урока. Билеты: 1. Дайте определение логарифмического уравнения. 2. Какими методами можно решать логарифмические уравнения? 3. 4. ...
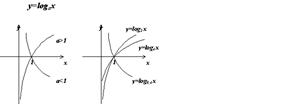
... функций, имеющих одинаковое основание, симметричны относительно прямой (рис. 3). Рис. 3 Глава 3. Тождественные преобразования показательных и логарифмических выражений на практике. Задание 1. Вычислите: 1.1) ; 1.2) ; 1.3) ; 1.4) ; 1.5) . Решение: 1.1) ; 1.2) ; 1.3) ; 1.4) ; 1.5) . Ответ: ; ; ; ; . Задание 2. Упростите выражения: 2.1) ; ...
... рассмотреть лишь два варианта: , и . Подставляя эти пары значений в остальные уравнения, убеждаемся, что первая из них дает искомое разложение: . Этот способ решения называется методом неопределенных коэффициентов. Если уравнение имеет вид , где и - многочлены, то замена сводит его решение к решению двух уравнений меньших степеней: и . Возвратные уравнения Возвратным алгебраическим ...
... . Частные случаи тригонометрических уравнений Определение. Уравнения вада sin x = a; cos x = a; tg x = a; ctg x = a, где x - переменная, aR, называются простейшими тригонометрическими уравнениями. Тригонометрические уравнения Аксиомы стереометрии и следствия из них Основные фигуры в пространстве: точки, прямые и плоскости. Основные свойства точек, прямых ...
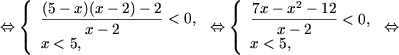
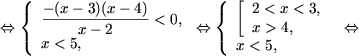
0 комментариев