Навигация
Функция не может иметь в одной точке два разных предела
1. Функция не может иметь в одной точке два разных предела.
2. ![]() , если C — постоянная функция.
, если C — постоянная функция.
3. Если существует![]() и C — постоянная функция, то
и C — постоянная функция, то
![]() .
.
4. Если существуют![]() и
и ![]() , то существует
, то существует ![]() , равный
, равный ![]() , а также существует
, а также существует ![]() , равный
, равный ![]() . Если при этом
. Если при этом ![]() , то существует
, то существует![]() , равный
, равный ![]() .
.
Число B называется пределом функции f(x) в точке a справа (это записывается в виде формулы ![]() ), если для любого положительного числа e найдется положительное число d, такое что из из условия 0 < x – a < d будет следовать êB –f(x) ê < e.
), если для любого положительного числа e найдется положительное число d, такое что из из условия 0 < x – a < d будет следовать êB –f(x) ê < e.
Согласно приведенному определению ![]() .
.
Число С называется пределом функции f(x) в точке b слева (это записывается в виде формулы ![]() ), если для любого положительного числа e найдется положительное число d такое, что из условия 0 < b – x < d будет следовать êC – f(x)ê < e.
), если для любого положительного числа e найдется положительное число d такое, что из условия 0 < b – x < d будет следовать êC – f(x)ê < e.
Функция f(x) называется непрерывной в точке a справа (непрерывной в точке b слева), если
![]() (
(![]() ).
).
Функция ![]() непрерывна справа в точке x=0.
непрерывна справа в точке x=0.
Функция называется непрерывной на замкнутом промежутке [a, b], если она непрерывна на открытом промежутке (a, b), непрерывна справа в точке a и непрерывна слева в точке b.
Для того, чтобы выполнялось равенство ![]() , необходимо и достаточно, чтобы одновременно выполнялись два равенства:
, необходимо и достаточно, чтобы одновременно выполнялись два равенства:
![]() ;
; ![]()
Число А называется пределом функции f(x) при х, стремящемся к бесконечности:
![]() ,
,
если для любого положительного числа e можно найти такое положительное число M (зависящее от e), что для всех чисел х, превосходящих М, выполняется условие:
½f(x) – A½ < e.
Пусть теперь функция f(x) определена на полу бесконечном промежутке
(–¥; х0). Число А называется пределом функции f(x) при х, стремящемся к минус бесконечности:
![]() ,
,
если для любого положительного числа e можно найти такое положительное число M (зависящее от e), что для всех чисел х, меньших, чем – М, выполняется условие:
½f(x) – A½ < e.
Два, так называемых, "замечательных предела".
1. ![]() . Геометрический смысл этой формулы заключается в том, что прямая
. Геометрический смысл этой формулы заключается в том, что прямая ![]() является касательной к графику функции
является касательной к графику функции ![]() в точке
в точке ![]() .
.
2. ![]() . Здесь e — иррациональное число, приблизительно равное 2,72.
. Здесь e — иррациональное число, приблизительно равное 2,72.
Вопросы для самопроверки.
1.Приведите пример функции, не имеющей предела в данной точке.
2.При каких условиях из существования пределов слева и справа следует существование предела функции в данной точке.
3.Какова связь между понятиями предела функции и бесконечно малой функции?
4.Какова связь между бесконечно малой и бесконечно большой функцией?
5.Приведите примеры бесконечно малых функций: эквивалентных, одного порядка, разного порядка малости.
6.Чему равен предел суммы четырех функций?
7.В чем различие между понятиями предела и непрерывности функции в точке?
8.При каких условиях непрерывна сложная функция?
ТЕМА7. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Понятие производной. Геометрический смысл. Правила вычисления производных. Производная сложной функции. Таблица производных. Производные высших порядков. Понятие дифференциала и его геометрический смысл. Применение дифференциала для приближенных вычислений. Инвариантность дифференциала. Формула Тейлора и остаточный член. Формула Тейлора для элементарных функций. применение для приближенного вычисления функций и пределов. содержащих неопределенность. Возрастание и убывание функций. Экстремумы. выпуклость, вогнутость, точки перегиба. асимптоты. Построение графиков.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Рассмотрим функцию y=f(x), непрерывную в некоторой окрестности точки x. Пусть Dx приращение аргумента в точке x. Обозначим через Dy или Df приращение функции, равное f(x+Dx) – f(x). Отметим здесь, что функция непрерывна в точке x, если в этой точке бесконечно малому приращению аргумента Dx соответствует бесконечно малое приращение функции Df.
Отношение Df /Dx, как видно из рисунка 1, равно тангенсу угла a, который составляет секущая MN кривой y = f(x) c положительным направлением горизонтальной оси координат.
Отношение Dy / Dx или, что то же самое (f(x + Dx) f(x)) / Dx, можно рассматривать при заданном x как функцию аргумента Dx. Эта функция не определена в точке Dx = 0. Однако её предел в этой точке может существовать.
Если существует предел отношения (f(x + Dx) – f(x)) / Dx в точке Dx = 0, то он называется производной функции y = f(x) в точке x и обозначается y¢ или f¢(x):
![]()
![]() .
.
Нахождение производной функции y = f(x) называется дифференцированием.
Если для любого числа x из открытого промежутка (a, b) можно вычислить f¢(x), то функция f(x) называется дифференцируемой на промежутке (a, b).
Геометрический смысл производной заключается в том, что производная функции f(x) в точке x равна тангенсу угла наклона касательной к графику функции в этой точке.
Производная это скорость изменения функции в точке x. Из определения производной следует, что f¢ (x) » Df / Dx, причем точность этого приближенного равенства тем выше, чем меньше Dx. Производная f¢ (x) является приближенным коэффициентом пропорциональности между Df и Dx.
Таблица производных элементарных функций.
| f(x) |
| f(x) |
| f(x) |
|
| C | 0 |
|
| cosx | -sinx |
| x | 1 | lnx | 1/x | tgx | 1/cos2x |
| xn | nxn-1 | ax | axlna | arcsina |
|
|
| 1/(2 |
|
| arccosa | - |
| 1/x | -1 / x2 | sinx | cosx | arctgx | 1/(1+x2) |
Основные свойства производной.
1. Если функция имеет производную в точке, то она непрерывна в этой точке.
2. Если существует f¢ (x) , и С ‑ произвольное число, то функция ![]() имеет производную: (Cf(x))¢ = Cf¢ (x).
имеет производную: (Cf(x))¢ = Cf¢ (x).
Похожие работы
... , заданного матрицей P= в пространстве R2. Решение. Составим характеристическое уравнение: |P – λ·E|== λ2-5 λ+4=0 Из квадратного уравнения найдем собственные значения линейного оператора λ1=1, λ2=4. Чтобы найти собственные векторы, решим матричные уравнения: (P – λ1 E) X=0 и (P – λ2 E) X=0 В развернутом виде и Соответствующие однородные системы ...
... 361. -370. Вычислить тройной интеграл по области V, ограниченной заданными поверхностями. 371. -380. Вычислить криволинейный интеграл второго рода вдоль заданной линии (для незамкнутых кривых направление обхода соответствует возрастанию параметра t или переменной x; для замкнутых кривых направление предполагается положительным). L– отрезок прямой, ...
... климатическом кадастре. 4. Виды наказаний за экологические преступления Эколого-правовая ответственность выступает важным звеном правового обеспечения рационального природопользования и охраны окружающей среды. В юридической литературе признано, что ответственность проявляется как "обязанность выполнять соответствующие нормы поведения и обязанность нести неблагоприятные последствия за их ...
... быть пассажирские пути и платформы, пассажирское здание и переходы, пути отстоя оборачивающихся пригородных и дальних конечных поездов, багажные и почтовые устройства. В данном курсовом проекте рассматривают вопросы организации работы участковой станции «Н». Содержание Введение 1 Общие вопросы работы станции 2 Оперативное руководство и планирование работы станции 3 Технология обработки ...

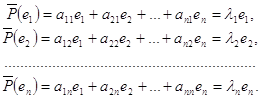
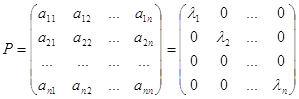
0 комментариев