Навигация
Построение экономико-математических моделей
Контрольная работа
по экономико-математическим методам
Задача №1
Условие задачи:
Администрация штата объявила торги на n строительных подрядов для n фирм. Ни с одной фирмой не заключается более одного контракта. По политическим соображениям чиновники администрации стремятся не заключать более N крупных контрактов с фирмами, расположенными за пределами штата. Обозначим через 1,2, …, s крупные контракты, а через 1,2,…,t - фирмы, расположенные за пределами штата. Целью является минимизация общих затрат при указанном условии. Постройте соответствующую данным условиям модель.
Решение:
Пусть х - затраты на строительство, тогда цель задачи "минимизация общих затрат" будет выражена через функцию
F = x → min
Пусть х1 - затраты на строительство при подряде местных строительных фирм, х2-затраты на строительство при подряде строительных фирм, расположенных за пределами штата.
F = n*х1+n*х2 → min
S*t ≤N
nn ≤1
х1, х2≥ 0
Задачу минимизации общих затрат на строительство можно записать как задачу математического программирования
n n t s
F =∑∑ Cij *Хij+∑∑ Cij*Yij → min
i=1 j=1 i=1 j=1
При ограничениях
Хij ≤ 1; I, j= 1, n
Yij ≤ 1; I, j= 1, n
∑ij≤ N; i=1, t; j=1s
Хij, Yij ≥0
Через Хij обозначен факт заключения администрацией штата с i - той фирмой, расположенной на территории штата, j - того контракта (подряда)
1, i - ая фирма заключила - контракт
Хij = 0, i - ая фирма не заключила - котракт
Через Yij обозначен факт заключения администрацией штата i - oй фирмой, расположенной за пределами штата, j - того контракта.
Через Cij обозначены затраты на строительство по j - тому контракту с i - ой фирмы.
Целевая функция представляет собой суммарные затраты. Первые два условия ограничивают количество заключаемых с одной строительной фирмой контрактов в количестве ≤ 1, третье условие ограничивает количество заключаемых контрактов с фирмами расположенными за пределами штата, в количестве не более N, четвертое условие очевидно исходя из условия данной задачи.
Задача № 2
Условие задачи:
На звероферме могут выращиваться черно-бурые лисицы и песцы. Для обеспечения нормальных условий их выращивания используется три вида кормов.
Количество корма каждого вида, которые должны ежедневно получать лисицы и песцы, приведено в таблице.
В ней же указаны общее количество корма каждого вида, которое может быть использовано зверофермой, и прибыль от реализации одной шкурки лисицы и песца.
| Вид корма | Кол-во единиц корма, которые ежедневно должны получать лисицы | Кол-во единиц корма, которые ежедневно должны получать песцы | Общее кол-во корма |
| 1 | 2 | 3 | 180 |
| 2 | 4 | 1 | 240 |
| 3 | 6 | 7 | 426 |
| Прибыль от реализации 1 шкурки | 16 | 12 |
Определить, сколько лисиц и песцов следует выращивать на звероферме, чтобы прибыль от реализации была максимальной.
Решение:
Введем переменные.
Пусть х - это количество лисиц и песцов, которое следует выращивать на ферме.
Х1 - это количество лисиц, которое следует выращивать на ферме.
Х2 - это количество песцов, которое следует выращивать на ферме.
Цель задачи: максимизация прибыли от реализации шкурок песцов и лисиц. Целевая функция:
F =16х1 + 12х2→ max
Посмотрим как будут выглядеть данные в задаче ограничения:
2х1+3х2≤180 - ограничения корма 1
4х1+х2 ≤ 240 - ограничения корма 2
6х1+7х2 ≤ 426 - ограничения корма 3
х1, х2≥ 0, ? Z
После решения задачи в программе XL получены результаты:
Похожие работы
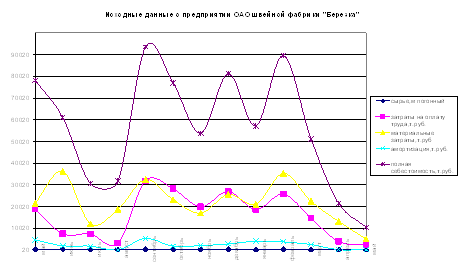
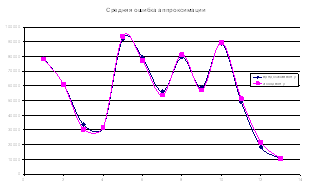
... и качественные характеристики этого элемента представлены ниже в таблице 1 за временной период с мая 2005 по май 2006. Для построения экономико-математической модели применен метод математической статистики. Расчеты по модели и анализ полученных результатов при использовании данного метода включает в себя этапы: 1.Графическое представление характеристик. 2.Предварительный статистический ...
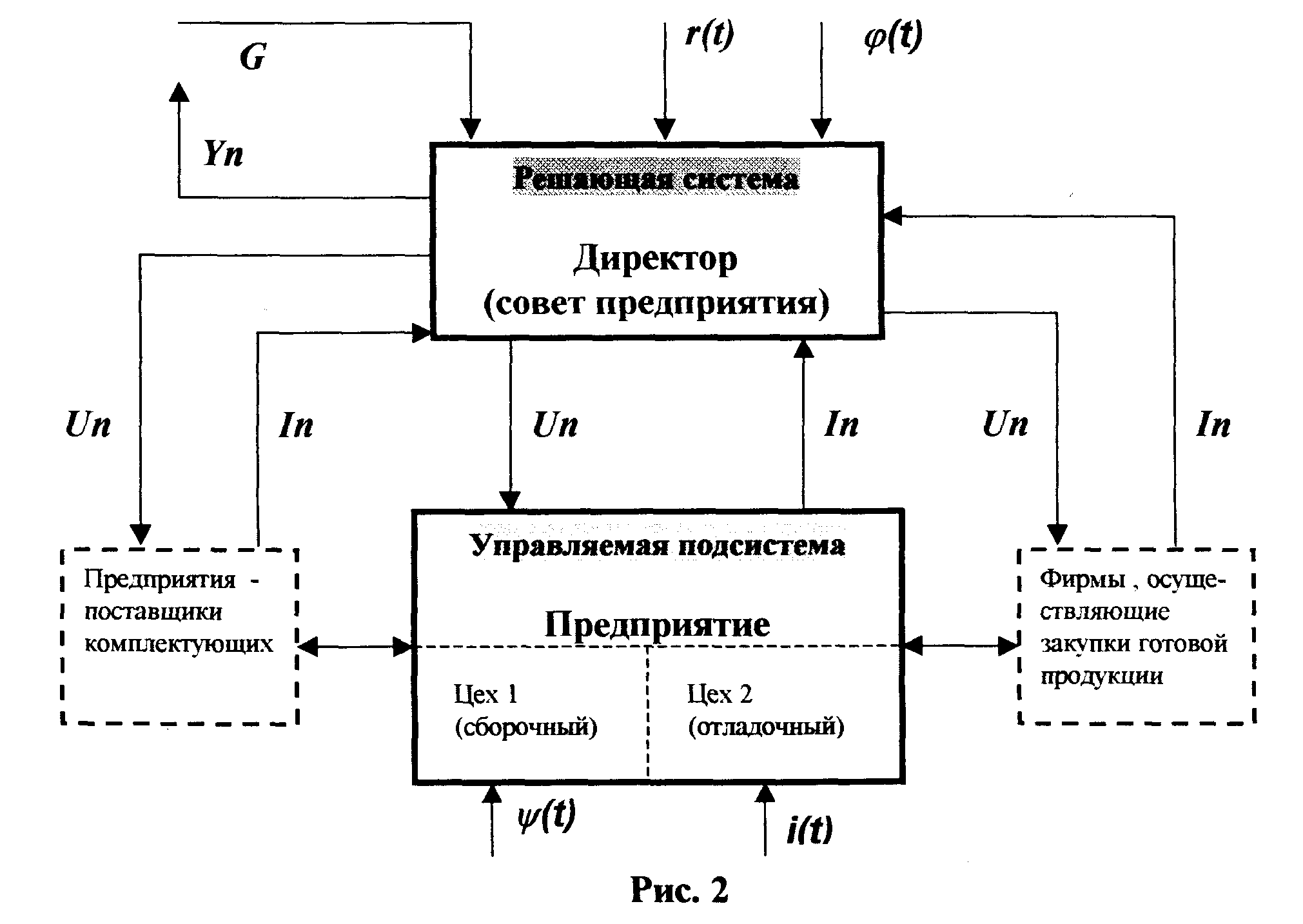
... на них, оценки технико-экономических показателей и, в завершении, построения экономико-математической модели предприятия. В экономико-математической модели в целевую функцию должен вводиться тот или иной фактор неопределенности. В дальнейшем будет приведена разработка методика учета факторов неопределенности, показаны математические модели снятия неопределенности. Крайне важным является оценка ...
... вопросы должны быть получены в ходе маркетинговых и проектно-изыскательских работ на фазе проектирования спортивных сооружений. И уже на этой стадии в процесс активно включаются экономико-математические методы, задействуется существующий аппарат математического моделирования и прогнозирования. Данные методы и расчеты совершенно необходимы для определения: сроков окупаемости отдельных предприятии ...
... моделей экстремальных планов и экстремальных значений целевой функции быть не может. Таким образом, для принятия оптимального решения любой экономической задачи необходимо построить ее экономико-математическую модель, по структуре включающую в себе систему ограничений, целевую функцию, критерий оптимальности и решение. Методика построения экономико-математической модели состоит в том, чтобы ...
0 комментариев