Навигация
Экономико-математическая модель
Экономико-математическая модель
Экономико-математическая модель – это выраженная в формально-математических терминах экономическая абстракция, логическая структура которой определяется как объективными свойствами предметами описания, так и субъективным целевым фактором исследования, для которого это описание предпринимается.
Между моделью и ее прототипом не может существовать взаимооднозначного соответствия, так как модель – это абстракция, связанная с обобщениями и потерей информации. Адекватность реальной действительности - основное требование ,предъявляемое к модели.
Конструктивно каждая математическая модель представляет собой совокупность взаимосвязанных математических зависимостей , отражающих определенные группы реальных экономических зависимостей.
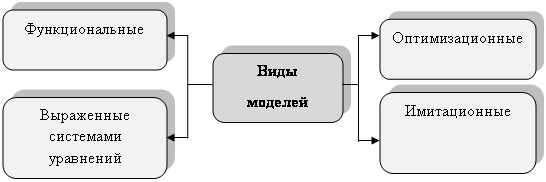
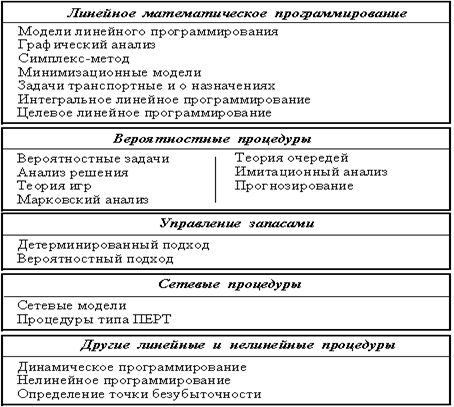
Классифицируются экономико-математические модели по различным признакам, в том числе и по математическому инструменту, применяемому при моделировании.
Наиболее распространенными и эффективными математическими методами, которые нашли как теоретическое, так и практическое приложение в экономических исследованиях, являются: дифференциальное исчисление, математическая статистика, линейная алгебра, математическое программирование и другие.
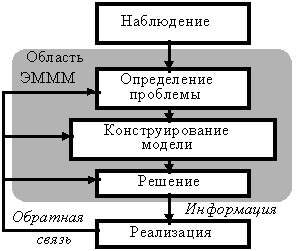
Порядок построения экономико-математической модели
Для построения экономико-математической модели определяется объект исследования: экономика государства в целом, отрасль, предприятие, цех и т.п.
Формулируется цель исследования.
В рассматриваемом экономическом объекте выделяются структурные и функциональные элементы и выделяются наиболее существенные качественные характеристики этих элементов, влияющие на достижения поставленной цели.
Вводятся символические обозначения для учитываемых характеристик экономического объекта. Определяется, какие из них будут рассматриваться как зависимые величины, а какие как независимые.
Формализуются взаимосвязи между определенными параметрами модели, т.е. строится собственно экономико-математическая модель.
Проводятся расчеты по модели и анализируются результаты полученных расчетов.
Если результаты оказываются неудовлетворительными с точки зрения неадекватности отображения моделируемого процесса или явления ,то происходит возврат к одному из предшествующих пунктов и процесс повторяется.
Пример экономико-математической модели
Структуру предприятия удобно описывать организационной моделью, которая демонстрирует состав функциональных подразделений предприятия и связи их подчинения и взаимодействия.
При функциональной организационной структуре предприятие подразделяется на элементы, каждый из которых имеет свои задачи и обязанности. Характеристики и особенности того или иного подразделения соответствуют наиболее важным направлениям деятельности предприятия.
Функциональная организационная модель предприятия на примере ОАО швейная фабрика «Березка»:

![]()


|
|
|
|
|
|

|
Такой вид организационной модели , как правило, встречается в крупных организациях, когда необходимо обеспечить слаженную совместную работу большого числа функциональных подразделений.
Объектом исследования будет являться швейная фабрика «Березка», целью исследования – оценка эффективности работы выпуска продукции. Более подробно для разрешения поставленной цели будем рассматривать функциональный и структурный элемент объекта - производство.
Наиболее существенные и качественные характеристики этого элемента представлены ниже в таблице 1 за временной период с мая 2005 по май 2006.
Для построения экономико-математической модели применен метод математической статистики.
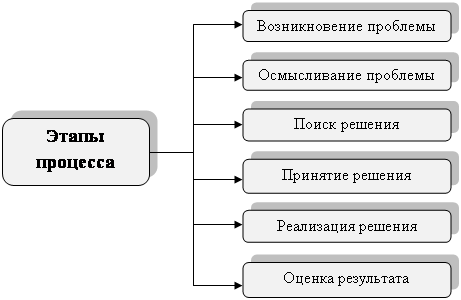
Расчеты по модели и анализ полученных результатов при использовании данного метода включает в себя этапы:
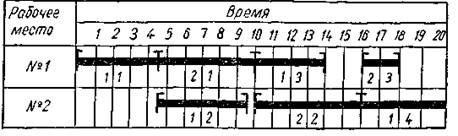
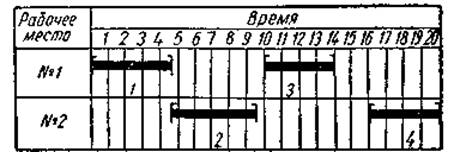
1.Графическое представление характеристик.
2.Предварительный статистический анализ(анализ данных по выборкам).
3.Корреляционный анализ данных.
4.Регрессионный анализ данных.
| сырье, м погонный | затраты на оплату труда, тыс.руб. | материальные затраты, тыс.руб | амортизация, тыс.руб. | полная себестоимость, тыс.руб | |
| май | 230 | 18729 | 21516 | 4642 | 78164 |
| июнь | 303 | 7415 | 36225 | 1951 | 61068 |
| июль | 102 | 7340 | 12064 | 1697 | 30564 |
| август | 175 | 3156 | 18770 | 120 | 31750 |
| сентябрь | 155 | 31854 | 32548 | 5364 | 93611 |
| октябрь | 195 | 28224 | 23190 | 1693 | 77059 |
| ноябрь | 112 | 19939 | 17061 | 2018 | 53794 |
| декабрь | 185 | 26850 | 25530 | 2811 | 81330 |
| январь | 98 | 18589 | 21042 | 4061 | 57179 |
| февраль | 248 | 25728 | 35358 | 3718 | 89639 |
| март | 111 | 14607 | 22426 | 2537 | 51239 |
| апрель | 68 | 3920 | 13190 | 118 | 21689 |
| май | 28 | 2347 | 5094 | 104 | 10510 |
Исходные данные ОАО швейная фабрика «Березка»
Таблица 1
Из исходных характеристик экономического объекта являются независимыми (Х1,Х2,Х3,Х4) или факторными признаками : сырье, затраты на оплату труда, материальные затраты, амортизация, а зависимой или результативным признаком (У) – полная себестоимость.
Похожие работы
... Теория очередей 59,7 Нелинейное программирование 46,8 Динамическое программирование 38,7 Теория игр 30,6 Следует отметить определенную переоценку значимости экономико-математических моделей в реальной практике управления экономико-производственными системами. Это связано с непреодолимыми пока сложностями моделирования процессов в экономико-производственных системах из-за непрерывности ...
... z = х47 - х45 -> шах. Глава 2. Определение структурных сдвигов и эффективности оптимального плана 2.1 Анализ оптимального решения экономико-математической модели оптимизации производственной структуры сельскохозяйственного предприятия Экономикс - математический анализ представляет собой заключительный этап математического моделирования экономических процессов, который основывается на ...
... ситуации является определяющим фактором [7]. В зависимости от того, какой метод анализа модели выбран, факторныe разложения могут различаться. Глава 2. Применение детерминированных экономико-математических моделей и методов факторного анализа на примере РУП «ГЗЛиН». 2.1 Характеристика РУП «ГЗЛиН» 9 октября 1979 - издан приказ М 272 Министерства машиностроения для животноводства и ...
... того чтобы получить оптимальное решение нужно перейти на лист «Расчет» через основное меню, нажав кнопку «Расчеты». На листе «Расчет» представлена математическая модель оптимизации распределения трудовых ресурсов (рис 3.3) описанная в разделе 3.2. Данная модель использует надстройку «Поиск решений» MS Excel Рис 3.3. Для запуска надстройки «Поиск решений» MS Excel, необходимо в главном меню ...
0 комментариев