Навигация
Лисиц и 12 песцов следует выращивать на звероферме, чтобы прибыль была максимальной
57 лисиц и 12 песцов следует выращивать на звероферме, чтобы прибыль была максимальной.
Задача № 3Условие задачи:
Найти оптимальное сочетание посевов трех продовольственных культур: озимой ржи, пшеницы, картофеля под посевы отведено 1000га пашни, которая должна использоваться полностью. При этом общие ресурсы труда составляют 30000 человек. Производство культур характеризуется показателями таблицы:
| показатели | Озимая рожь | Озимая пшеница | картофель |
| Урожайность с 1га, ц | 32 | 40 | 250 |
| Затраты труда на 1га, человек | 16 | 20 | 80 |
| Материально-денежные затраты на 1га, руб | 214 | 226 | 782 |
По плану требуется произвести 32000ц зерна, 40000ц картофеля. Критерий оптимизации - минимизация денежно-материальных затрат на производство продукции. Решить прямую и двойственную задачи. Провести послеоптимизационный анализ.
Прямая задача:
Пусть х - это количество га занятых под продовольственные культуры, тогда Х1 - кол-во га, занятых под озимой рожью, Х2 - кол-во га, занятых под озимой пшеницей, Х3 - кол-во га, занятых под картофелем.
Целью задачи является - минимизация денежно-материальных затрат на производство продукции, т.е.
F = 214x1+226x2+782x3 → min
Выделим ограничения, определенные условиями задачи:
x1+x2+x3=1000,16x1+20x2+80x3≤ 30000,32x1+40x2 ≥ 32000,250x3 ≥ 40000,x1, x2, x3 ≥ 0.
Решаем задачу в программе XL и получаем результат:
Х1, т. е количество га, занятых под озимой рожью=125га.
Х2, т. е количество занятых га под озимую пшеницу =700га.
Х3, т. е количество занятых га под картофель=175га.
Это будет оптимальное сочетание посевов трех продовольственных культур. Затраты на производство продукции составили 825руб.
Двойственная задача:
На первом этапе приведем прямую задачу к двойственной задачи.
х1+x2+x3 ≥1000
х1+x2+x3 ≤ 1000
16x1+20x2+80x3 ≤ 30000
32x1+40x2 ≥ 32000
250x3 ≥ 40000
x1 x2 x3 ≥ 0
матрица ограничений. Умножаем на - 1.
x1-x2-x3 ≤-1000
x1+x2+x3 ≤ 1000
16x1+20x2+80x3 ≤ 30000
32x1-40x2 ≤ - 32000
250x3 ≤ - 40000
x1, x2,x3 ≥ 0
транспонированная матрица коэффициентов ограничения
х1 х2 х3
у1 - 1 - 1 - 1 - 1000
у2 1 1 1 1000
у3 16 20 80 30000
у4 - 32 - 40 0 - 32000
у5 0 0 - 250 – 40000
Целевая функция двойственной задачи будет выглядеть следующим образом:
Z = - 1000y1 +1000y2 + 30000y3 - 32000y4 - 40000y5 → max
y1+y2+16y3-32y4 ≤ 214
y1+y2+20y3-40y4 ≤ 226
y1+y2+80y3-250y5 ≤ 782
решаем ограничения в программе XL
Похожие работы
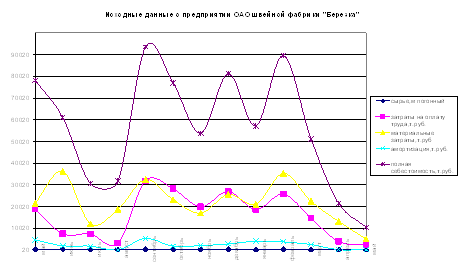
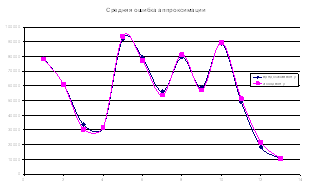
... и качественные характеристики этого элемента представлены ниже в таблице 1 за временной период с мая 2005 по май 2006. Для построения экономико-математической модели применен метод математической статистики. Расчеты по модели и анализ полученных результатов при использовании данного метода включает в себя этапы: 1.Графическое представление характеристик. 2.Предварительный статистический ...
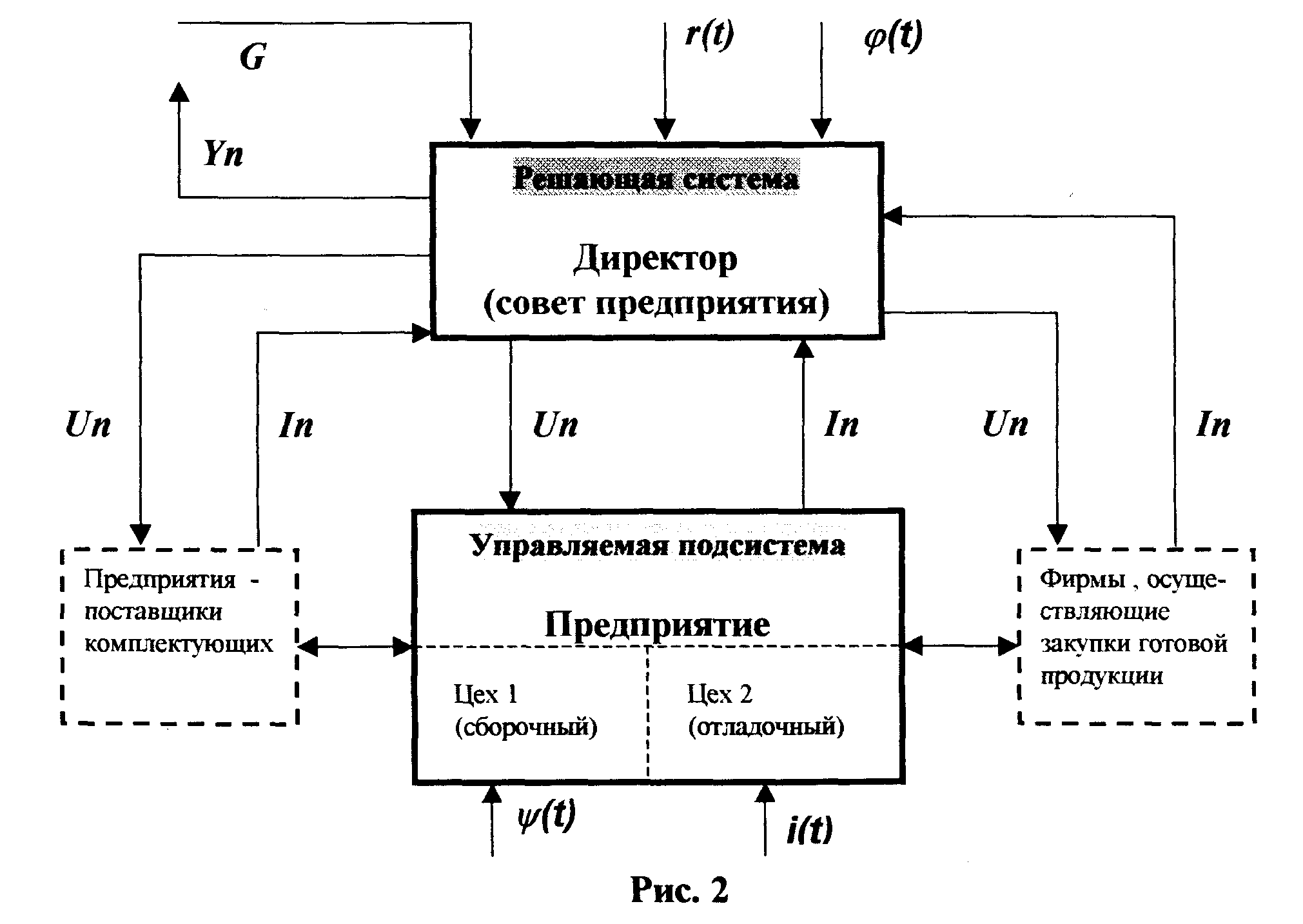
... на них, оценки технико-экономических показателей и, в завершении, построения экономико-математической модели предприятия. В экономико-математической модели в целевую функцию должен вводиться тот или иной фактор неопределенности. В дальнейшем будет приведена разработка методика учета факторов неопределенности, показаны математические модели снятия неопределенности. Крайне важным является оценка ...
... вопросы должны быть получены в ходе маркетинговых и проектно-изыскательских работ на фазе проектирования спортивных сооружений. И уже на этой стадии в процесс активно включаются экономико-математические методы, задействуется существующий аппарат математического моделирования и прогнозирования. Данные методы и расчеты совершенно необходимы для определения: сроков окупаемости отдельных предприятии ...
... моделей экстремальных планов и экстремальных значений целевой функции быть не может. Таким образом, для принятия оптимального решения любой экономической задачи необходимо построить ее экономико-математическую модель, по структуре включающую в себе систему ограничений, целевую функцию, критерий оптимальности и решение. Методика построения экономико-математической модели состоит в том, чтобы ...
0 комментариев