Навигация
Теоретическое обоснование. Общие вопросы
3. Теоретическое обоснование. Общие вопросы
Сеть (транспортная сеть) – частный случай ориентированного графа. Транспортная сеть G=( V,E) – ориентированный граф, в котором каждое ребро имеет неотрицательную пропускную способность. Выделяются две вершины: источник v и сток u такие, что любая другая вершина сети лежит на пути из v в u. v – это единственная вершина (v – источник ), которая не содержит входящих дуг , а содержит только выходящие дуги. u – это единственная вершина (u - сток), которая не содержит выходящих дуг. Все остальные вершины – промежуточные вершины. Для любой промежуточной вершины существует путь из источника в сток. Сеть не содержит контуров. Если для сети указаны пропускные способности, то такая сеть называется транспортной сетью.
Поток – это определенная величина на дуге е. Поток в сети G=( V,E) – это функция f, заданная на дугах сети, значение на дуге е – это величина на дуге е. Для всех промежуточных вершин соответствует сумма величин потоков на дугах входящих в вершину w, которая равна выходящему из вершины потоку.
![]()
Величина потока в сети.
Величина всего потока в сети модуля равна сумме величин потока выходящих из источника или сумме входящих величин потока входящих в сток.
![]()
Поток минимальной стоимости – задача о потоке минимальной стоимости состоит в нахождении самого дешевого способа передачи определенного количества потока через транспортную сеть.
Обозначения:
Для всех дуг имеется пропускная способность: ![]()
Стоимость пересылки единицы потока по дуге e: C(e)
Накладываются следующие условия:
1. Ограничение пропускной способности ![]() . Поток не может превысить пропускную способность.
. Поток не может превысить пропускную способность.
2. Антисимметричность: ![]() . Поток из u в v должен быть противоположен потоку из v в u.
. Поток из u в v должен быть противоположен потоку из v в u.
![]()
4. Описание алгоритма нахождения потока минимальной стоимости
Вход: транспортная сеть G=( V,E)с пропускной способностью дуг B(e)
Выход: максимальный поток с минимальной стоимостью.
Идея: Каждая итерация ставит своей целью увеличить поток в сети. Для этих целей предназначен инкрементальный граф, который позволяет увеличить поток на некоторую фиксированную величину. Наличие прямых дуг позволяет увеличить поток на соответствующей дуге сети. Обратная дуга уменьшает поток. Алгоритм заканчивается когда в инкрементальном графе нет пути от источника к стоку.
Алгоритм:
Шаг 0
Данный шаг осуществляется только один раз. Вначале мы присваиваем всем дугам нулевой поток: ![]()
Шаг 1
Для текущего потока строится инкрементальный граф. Прямые дуги имеются, если поток на этой дуге меньше, чем пропускная способность:
![]()
Обратные дуги (дуги противоположны по отношению к ориентации прямых дуг) имеются, если на дугах имеется поток.
![]()
Каждой дуге переписываем стоимость дуги. Если е прямая, то длинна, равна стоимости пересылки, если е обратная, то ее длинна – это стоимость, но при отрицательном значении.
Назначаем длины дуг для инкрементального графа:
· Для прямой дуги: e:C(e)
· Для обратной дуги: e: - C(e)
Шаг 2
Нахождение кратчайшего пути в инкрементальном графе из источника v в сток u. Если такого пути нет, то происходит конец алгоритма. Найденный путь является максимальным.
Шаг 3
Нахождение минимального Δ. Просматриваем дуги кратчайших путей в инкрементальном графе. Для каждой дуги определяем величину Δ.
Для каждой прямой дуги:
![]()
Для каждой обратной дуги:
![]()
Величина, на которую можно увеличить поток. Находим минимальное значение на всех этих дугах.
![]()
Шаг 4
Наращивание потока в сети. Корректируем поток на дугах в соответствии последнего пути в инкрементальном графе.
На этих дугах, поток изменяется по правилам:
Для прямых дуг:
![]()
Для обратных дуг:
![]()
Алгоритм завершается, если заданная величина потока достигнута.
Переход к шагу 1.
Похожие работы
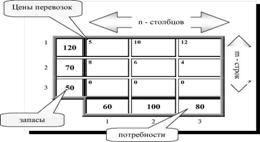
... сразу же составлен план перевозок, удовлетворяющий балансовым условиям. Полученное решение является опорным решением транспортной задачи. Составленный нами план перевозок, не является оптимальным по стоимости, так как при его построении мы совсем не учитывали стоимость перевозок Сij . 3. Метод потенциалов. Пусть имеется транспортная таблица, соответствующая начальному решению, хil= для ...
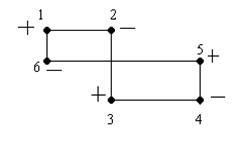
... . Система векторов условий транспортной задачи линейно независима тогда и только тогда, когда из соответствующих им клеток таблицы нельзя образовать ни одного цикла. Следовательно, допустимое решение транспортной задачи , i=1,2,…,m; j=1,2,…,n является опорным только в том случае, когда из занятых им клеток таблицы нельзя образовать ни одного цикла. Метод вычеркивания. Для проверки возможности ...
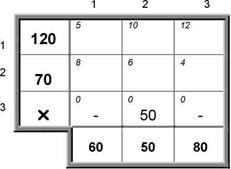
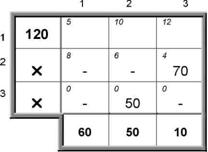
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... ). Требуется распределить все работы между всеми рабочими так, чтобы время выполнения работ было минимальным, а каждую работу выполнял только один рабочий. §4. Решение транспортной задачи в Excel В качестве примера я рассмотрел транспортную задачу для 2 складов и 5 магазинов. · В ячейки C4:C5 записал объемы продукции, имеющиеся на 2 складах. · В ячейки E5:I5 - заявки на продукцию, ...
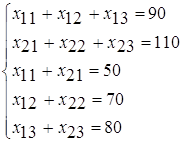





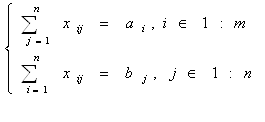
0 комментариев