Навигация
Решение транспортной задачи методом потенциалов
Курсовая работа
на тему:
"Решение транспортных задач
методом потенциалов"
Содержание.
1. Линейная транспортная задача
2. Составление опорного плана
3. Метод потенциалов
3. Список использованной литературы
1. Транспортная задача.
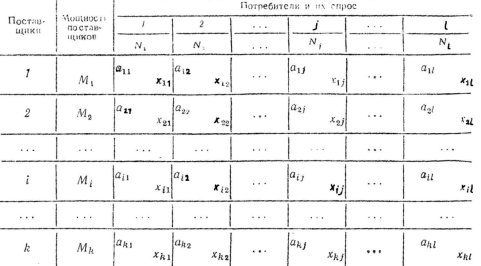
Транспортная задача ставится следующим образом: имеется m пунктов отправления, в которых сосредоточены запасы каких-то однородных грузов. Имеется n пунктов назначения подавшие заявки соответственно на груза. Известны стоимости р ijперевозки единицы груза от каждого пункта отправления до каждого пункта назначения. Все числа р ij, образующие прямоугольную таблицу заданы. Требуется составить такой план перевозок (откуда, куда и сколько единиц поставить), чтобы все заявки были выполнены, а общая стоимость всех перевозок была минимальна.
Далее, предполагается, что ![]() 1
1
где bi есть количество продукции, находящееся на складе i, и aj – потребность потребителя j.
Замечание. Если ![]() то количество продукции, равное
то количество продукции, равное ![]() остается на складах. В этом случае мы введем "фиктивного" потребителя n +1 с потребностью
остается на складах. В этом случае мы введем "фиктивного" потребителя n +1 с потребностью ![]() и положим транспортные расходы pi,n+1 равными 0 для всех i.
и положим транспортные расходы pi,n+1 равными 0 для всех i.
Если ![]() то потребность не может быть покрыта. В этом случае начальные условия должны быть изменены таким образом, чтобы потребность в продукции могла быть обеспечена.
то потребность не может быть покрыта. В этом случае начальные условия должны быть изменены таким образом, чтобы потребность в продукции могла быть обеспечена.
Обозначим через xij количество продукции, поставляемое со склада i потребителю j. В предложении (1) нам нужно решить следующую задачу (математическая модель транспортной задачи):
![]()
![]() 2
2
![]()
![]()
![]()
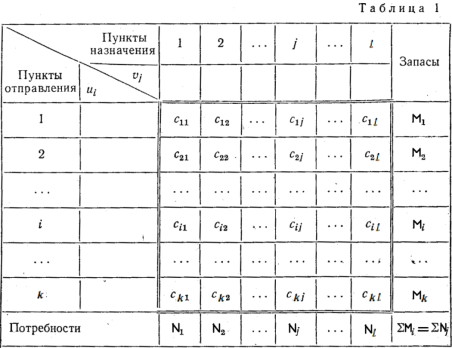
Транспортную задачу мы можем характеризовать транспортной таблицей и таблицей издержек:
|
| а1 | … | аn | |||
| b1 . . . bm | . |
|
|
|
|
|
|
| . |
|
|
|
| |
|
|
| . |
|
|
| |
|
|
|
| . |
|
| |
|
|
|
|
| . |
| |
|
|
|
|
|
| . | |
| p11 | … | p1n |
| . |
| . |
| . |
| . |
| . |
| . |
| pm1 | … | pmn |
Допустимый план перевозок будем представлять в виде транспортной таблицы:
|
| а1 | … | аn |
| b . . . bm |
| … |
|
| . |
| . | |
| . |
| . | |
| . |
| . | |
|
| … |
|
Cумма элементов строки i должна быть равна bi, а сумма элементов столбца j должна быть равна aj, и все ![]()
![]() должны быть неотрицательными.
должны быть неотрицательными.
Пример 1.
|
| 20 | 5 | 10 | 10 | 5 |
| 15 |
|
|
|
|
|
| 15 |
|
|
|
|
|
| 20 |
|
|
|
|
|
| 5 | 6 | 3 | 5 | 9 |
| 6 | 4 | 7 | 3 | 5 |
| 2 | 5 | 3 | 1 | 8 |
Мы получаем следующую задачу:
х11+х12+х13+х14+х15 =15,
х21+х22+х23+х24+х55 =15,
х31+х32+х33+х34+х35 =20,
х11 +х21 +х31 =20,
х12 +х22 +х32 =5,
х13 +х23 +х33 =10,
х14 +х24 +х34 =10,
х15 +х25 +х35 =5;
хij![]() 0 для i = 1,2,3; j = 1,2,3,4,5;
0 для i = 1,2,3; j = 1,2,3,4,5;
Кmin=5х11+6х12+3х13+5х14+9х15+6х21+4х22+7х23+3х24+5х25+2х31+5х32+3х33+х34+8х35;
Такие задачи целесообразно решать при помощи особого варианта симплекс-метода – так называемого метода потенциалов.
Все транспортные задачи имеют оптимальное решение. Если все значение aj и biв условиях транспортной задачи целочисленные, то переменныеxij во всех базисных решениях (а так же и в любом оптимальном базисном решении) имеют целочисленные значения.
Похожие работы
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
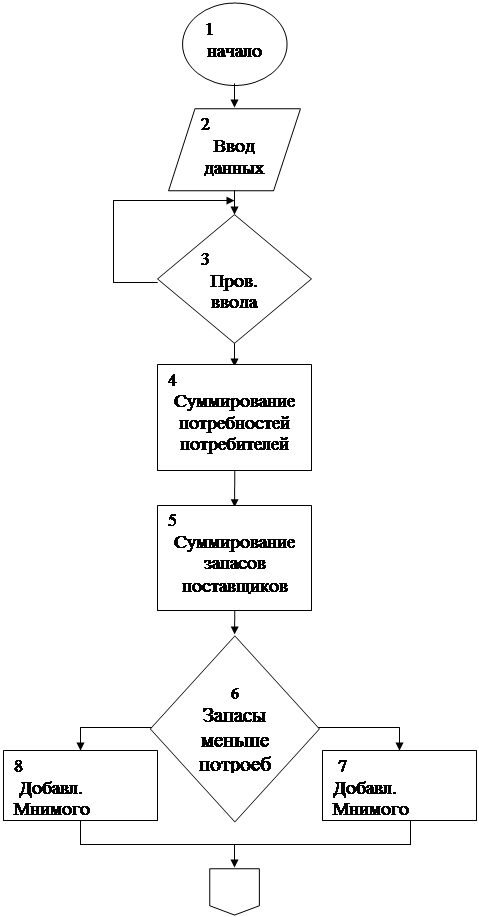
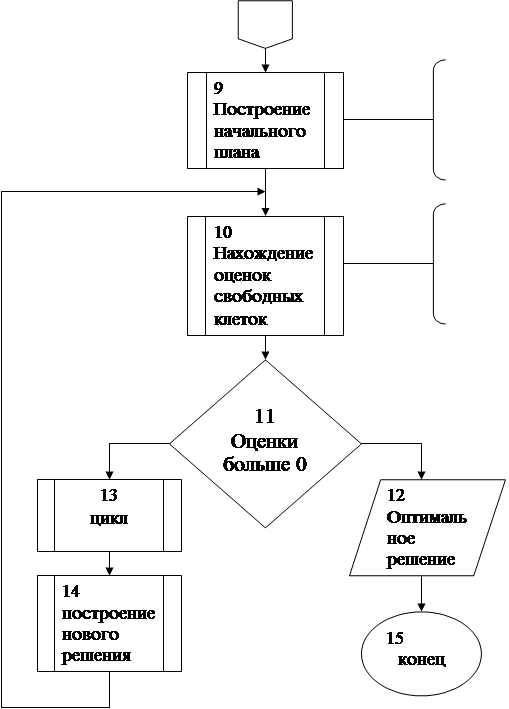
... метод потенциалов. Однако на распределительном методе основаны некоторые другие способы решения задач, что и вызывает необходимость его изучения. [5] 9. Метод потенциалов Решение транспортной задачи любым способом производится на макете. Макет для применения метода потенциалов имеет следующий вид. Основная часть макета выделена двойными линиями. Она содержит k×l клеток. Каждая ...
... Ai в Bj равна Cij; таблица стоимостей задана. Требуется найти план перевозок xij, который удовлетворял бы балансовым условиям и при этом стоимость всех перевозок бала минимальна. Идея метода потенциалов для решения транспортной задачи сводиться к следующему. Представим себе что каждый из пунктов отправления Ai вносит за перевозку единицы груза (всё равно куда) какую-то сумму ai; в свою ...
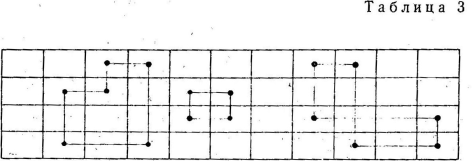
... . Система векторов условий транспортной задачи линейно независима тогда и только тогда, когда из соответствующих им клеток таблицы нельзя образовать ни одного цикла. Следовательно, допустимое решение транспортной задачи , i=1,2,…,m; j=1,2,…,n является опорным только в том случае, когда из занятых им клеток таблицы нельзя образовать ни одного цикла. Метод вычеркивания. Для проверки возможности ...





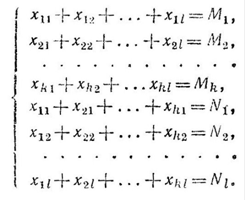

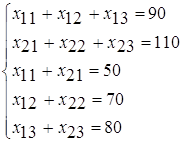
0 комментариев