Навигация
Решение индивидуального задания по шагам
5. Решение индивидуального задания по шагам
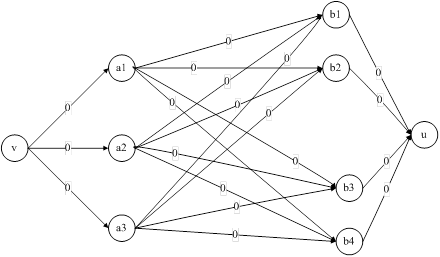
![]()
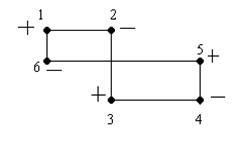
Рис. 2. Нулевой поток.
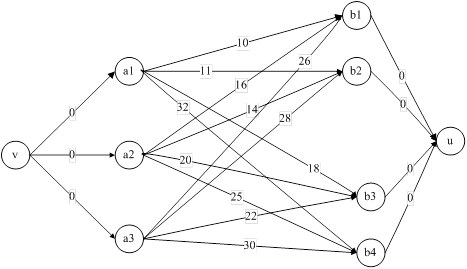
![]()
Рис.3. Инкрементальный граф
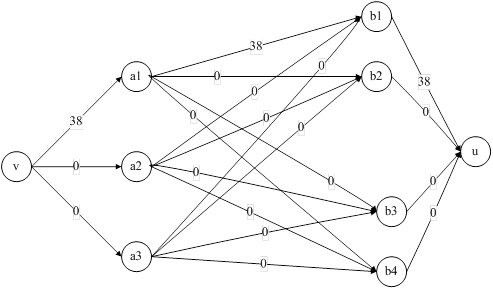
![]()
Рис. 4. Увеличения потока в сети
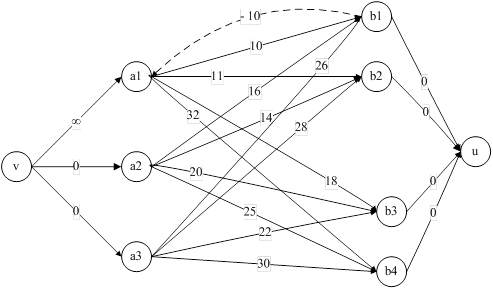
![]()
Рис.5. Инкрементальный граф
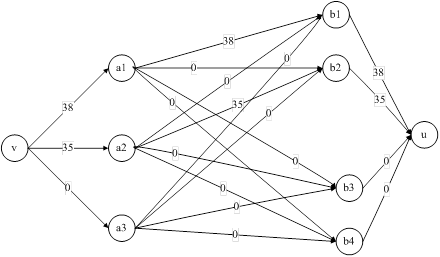
![]()
Рис. 6. Увеличение потока в сети
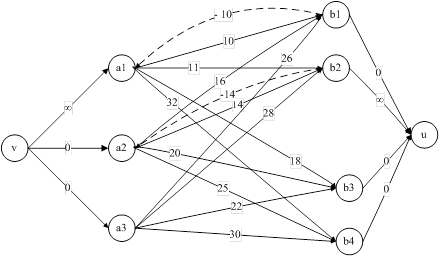
![]()
Рис.7. Инкрементальный граф
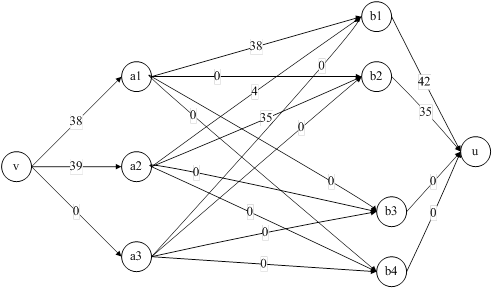
![]()
Рис. 8. Увеличение потока в сети
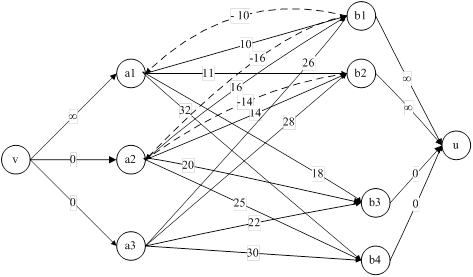
![]()
Рис.9. Инкрементальный граф
![]()
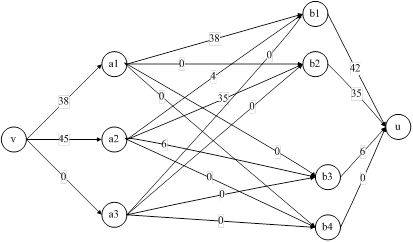
Рис. 10. Увеличение потока в сети
![]()
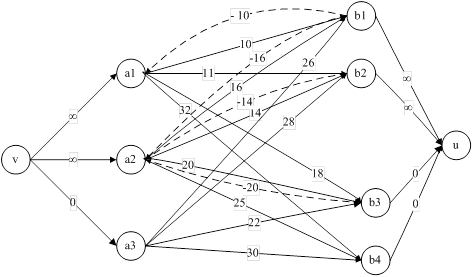
Рис.11. Инкрементальный граф
![]()
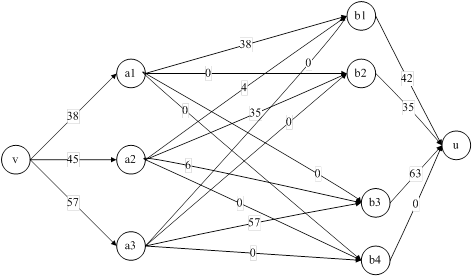
Рис. 12. Увеличение потока в сети

![]()
Рис.13. Инкрементальный граф
![]()
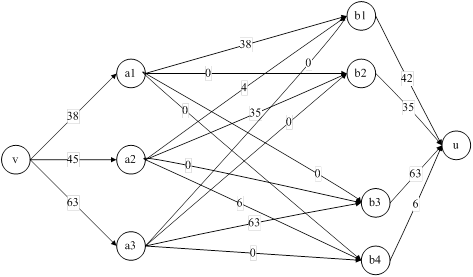
Рис. 14. Увеличение потока в сети
![]()
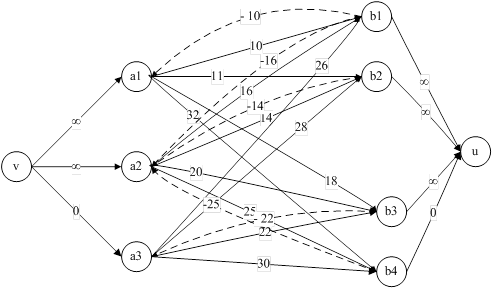
Рис. 15. Инкрементальный граф
![]()
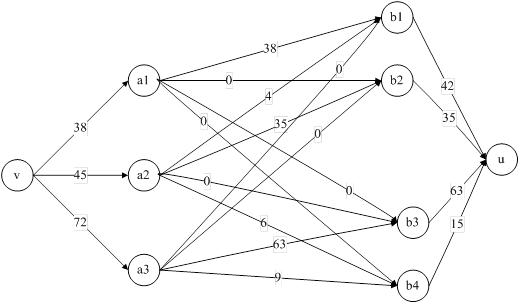
Рис. 16. Увеличение потока в сети. Конец алгоритма.
6. Программа (Mathcad)
Исходные данные:
· Число вершин n=9
· Очень большое число q=∞
· Заданная величина потока Givenflof =155
Пропускная способность дугСтоимость пересылки по дугам


Где, P – поток в сети; Tekflow – текущая величина потока, Givenflofw – заданная величина потока, Vect – величина на данной дуге, L -метки

7. Результаты программы

Величина потока
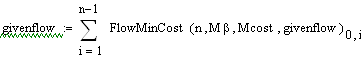
![]()
Стоимость потока
Price – стоимость
![]()
![]()
8. Конечный результат программы
Данная программа была решена двумя способами: в ручную и в среде MathCad. Результаты решения обеих вариантов совпадают, значит, можно сделать вывод о том, что поставленная транспортная задача, была решена, верно. По результатам вычислений, можно составить следующий план перевозок:

Рис. 17. Конечный результат
Потребитель b1 получает от поставщика a1 38 единиц товара
Потребитель b1 получает от поставщика a2 4 единиц товара
Потребитель b2 получает от поставщика a2 35 единиц товара
Потребитель b4 получает от поставщика a2 6 единиц товара
Потребитель b3 получает от поставщика a3 63 единиц товара
Потребитель b4 получает от поставщика a3 9 единиц товара
У поставщика а3 осталось 25 единиц товара не реализовано
Из выше перечисленного следует следующая реализация единиц ресурсов:
| Поставщики (реализованные ресурсы) | Потребители, которые получают от соответствующего поставщика ресурсы |
| а1 – 100% | b1 |
| а2 – 100% | b1, b2, b4 |
| а3 – 74,22% | b3, b4 |
Из приведенной таблицы видно, что два первых поставщика (а1 и а2) полностью реализуют поставки выделенных ресурсов. У третьего поставщика (а3) в наличии еще 25,77% единиц не реализованной продукции.
Общая стоимость:
С(![]() ) = 38*10 + 4*16 + 35*14 + 6*25 + 63*22 + 9*30 = 380 + 64 + 490 + 150 + 1386 + 270 = 2740
) = 38*10 + 4*16 + 35*14 + 6*25 + 63*22 + 9*30 = 380 + 64 + 490 + 150 + 1386 + 270 = 2740
9. Вывод
По окончанию данной работы я могу сказать, что данная работа была для меня как интересной, так и полезной. Благодаря ней я лучше научилась разбираться в транспортных задачах, в потоках и сетях. Сама задача мне не показалась достаточно сложной, при ее выполнение особых проблем не возникало. Также в данном курсе нас познакомили с такой средой как MathCad. Одной из главных задач данной работы было решение и сравнение транспортной задачи вручную и в среде MathCad. Подводя итоги данной работы, я убедилась, что задача была решена, верно, так как решение совпадает. Но стоит сказать, что решение данной задачи вручную мне понравилось гораздо больше, так как здесь пришлось анализировать различные факторы при нахождении минимального пути. Я надеюсь, что данная работа помогла мне лучше разобраться в данной теме.
Похожие работы
... сразу же составлен план перевозок, удовлетворяющий балансовым условиям. Полученное решение является опорным решением транспортной задачи. Составленный нами план перевозок, не является оптимальным по стоимости, так как при его построении мы совсем не учитывали стоимость перевозок Сij . 3. Метод потенциалов. Пусть имеется транспортная таблица, соответствующая начальному решению, хil= для ...
... . Система векторов условий транспортной задачи линейно независима тогда и только тогда, когда из соответствующих им клеток таблицы нельзя образовать ни одного цикла. Следовательно, допустимое решение транспортной задачи , i=1,2,…,m; j=1,2,…,n является опорным только в том случае, когда из занятых им клеток таблицы нельзя образовать ни одного цикла. Метод вычеркивания. Для проверки возможности ...
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... ). Требуется распределить все работы между всеми рабочими так, чтобы время выполнения работ было минимальным, а каждую работу выполнял только один рабочий. §4. Решение транспортной задачи в Excel В качестве примера я рассмотрел транспортную задачу для 2 складов и 5 магазинов. · В ячейки C4:C5 записал объемы продукции, имеющиеся на 2 складах. · В ячейки E5:I5 - заявки на продукцию, ...





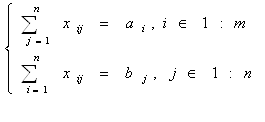
0 комментариев