Навигация
Кривошипно-ползунный механизм, его структура, схема, анализ
1. Структурный анализ механизма
Представлен кривошипно-ползунный механизм.
Число степеней исследуемого механизма определим по формуле Чебышева:
![]() (1)
(1)
где n – число подвижных звеньев в составе исследуемой кинематической цепи; p4 и p5 – соответственно число пар четвертого и пятого класса.
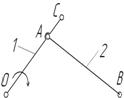
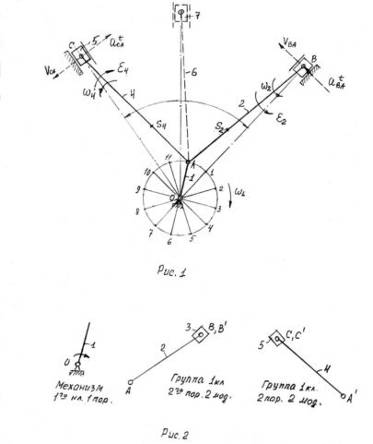
Для определения величины коэффициента n проанализируем структурную схему механизма (рисунок 1):
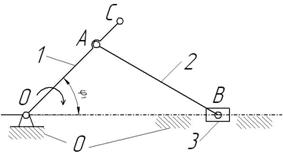
Рисунок 1 – Структурная схема механизма
Структурная схема механизма состоит из четырех звеньев:
1 – кривошип,
2 – шатун АВ,
3 – ползун В,
0 – стойка,
при этом звенья 1 – 3 являются подвижными звеньями, а стойка 0 – неподвижным звеном. Она представлена в составе структурной схемы двумя шарнирно-неподвижными опорами и направляющей ползуна 3.
Следовательно, n=3.
Для определения значений коэффициентов p4 и p5 найдем все кинематические пары, входящие в состав рассматриваемой кинематической цепи. Результаты исследования заносим в таблицу 1.
Таблица 1 – Кинематические пары
| № | Кинематическая пара (КП) | Схема кинема- тической пары | Класс кинема- тической пары | Степень подвиж- ности | ||||||
| 1 | 0 – 1 |
| 5 вращательная | 1 | ||||||
| 2 | 1 – 2 |
| 5 вращательная | 1 | ||||||
| 3 | 2 – 3 |
| 5 вращательная | 1 | ||||||
| 4 | 3 – 0 |
| 5 вращательная | 1 |
| ||||
Из анализа данных таблицы 1 следует, что исследуемый механизм ДВС с увеличенным ходом поршня состоит из семи пар пятого класса и образует замкнутую кинематическую цепь. Следовательно, p5=4, а p4=0.
Подставив найденные значения коэффициентов n, p5 и p4 в выражение (1), получим:
![]() (1)
(1)
Для выявления структурного состава механизма разбиваем рассматриваемую схему на структурные группы Ассура.
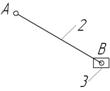
Первая группа звеньев 0-3-2 (рисунок 2).
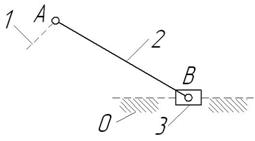
Рисунок 2 – Структурная группа Ассура
Данная группа состоит из двух подвижных звеньев:
шатун 2 и ползун 3;
двух поводков:
кривошип 1 и направляющая (стойка) 0;
и трех кинематических пар:
1-2 – вращательная пара пятого класса;
2-3 – вращательная пара пятого класса;
3-0 – поступательная пара пятого класса;
тогда n=2; p5=3, a p4=0.
Подставив выявленные значения коэффициентов в выражение (1),
получим:
![]()
Следовательно, группа звеньев 4-5 является структурной группой Ассура 2 класса 2 порядка 2 вида.
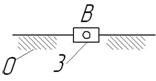
Вторая группа звеньев 0-1 (рисунок 3).
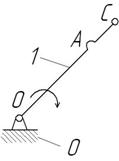
Рисунок 3 – Первичный механизм
Данная группа звеньев состоит из подвижного звена – кривошипа 1, стойки 0 и одной кинематической пары:
0 – 1 – вращательная пара пятого класса;
тогда n=1; p5=1, a p4=0.
Подставив найденные значения в выражение (1), получим:
![]()
Следовательно, группа звеньев 1 – 2 действительно является первичным механизмом с подвижностью 1.
Структурная формула механизма
МЕХАНИЗМ=ПМ(W=1) + СГА(2 класс, 2 порядок, 2 вид)
Похожие работы
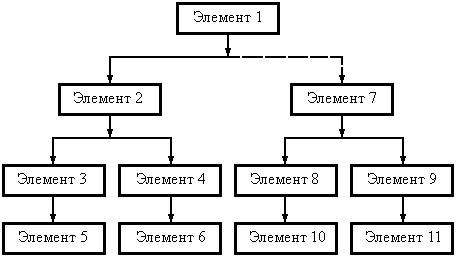
... б) с точечным формообразующим контактом 1 2 силовое 5 Плоская а) обычная б) с пальцем 3 2 Силовое Силовое и геометрическое 4. СТРУКТУРНЫЕ СВОЙСТВА МЕХАНИЗМОВ 4.1. Сложность N механизма. В металлорежущих станках сложные подвижные механические системы, передающие движения от входного звена к выходному (шпиндель, суппорт и ...
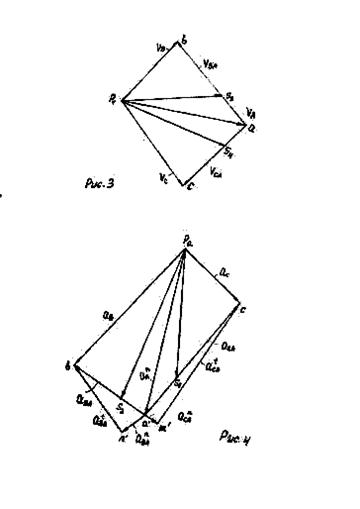
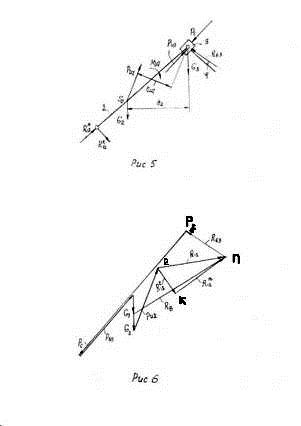
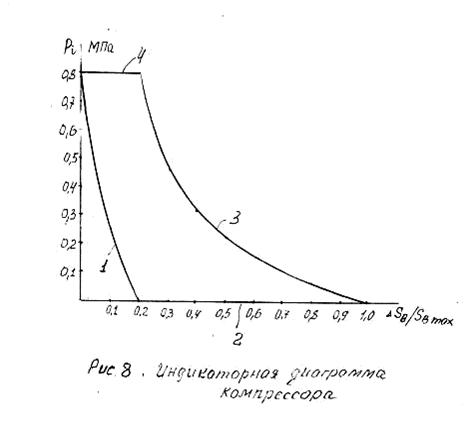
... отрезка "ав". Соединив точки S2 и S4 с полюсом плана скоростей получим векторы скоростей этих точек, а величина скоростей определится из соотношений: . Построенный план скоростей для механизма компрессора позволяет определить угловые скорости звеньев 2 и 4 в их вращательном движении. Как уже говорилось, отрезок плана скоростей ав (вектор) обозначает скорость точки "В" относительно точки ...
... обеспечивающим выполнение технологического процесса сшивания материалов и входящим в число исходных данных для выполнения прочностных расчетов игл. Угол заточки иглы . Общая длина лезвия иглы от острия до колбы: l1=L-(l2+l3) мм (1.1) L – общая длина иглы: в универсальных швейных машинах L=38 мм l2 – длина колбы, выступающая из игловодителя: в зависимости от лапки принимает- ся ...
... , , . Произведем оценку числа возможных вариантов, которые можно синтезировать на основе морфологической матрицы при наложении на нее граничных условий проектирования, а именно исключения вышеперечисленных вариантов: Для всего PC машины поточной линии прядильного производства оценка полных решений может быть проведена по следующей формуле: , где – количество исполнительных механизмов в ...
0 комментариев