Навигация
Определение сил, действующих на звенья механизма
4. Определение сил, действующих на звенья механизма
На каждое звено плоского рычажного механизма действует сила тяжести, которая находится по формуле:
![]() (23)
(23)
где g=9,81 м/с2 - ускорение свободного падения, а ![]() - масса i-го звена.
- масса i-го звена.
Для определения массы каждого звена плоского рычажного механизма воспользуемся следующими формулами:
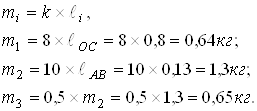 (24)
(24)
Далее определяем силы тяжести для каждого звена плоского рычажного механизма:
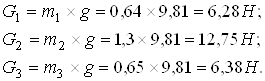
![]() (25)
(25)
Также мы можем определить силы инерции, действующие на звенья плоского рычажного механизма, по формуле:
![]() (26)
(26)
где ![]() - масса i-го звена, а
- масса i-го звена, а ![]() - ускорение центра масс i-го звена.
- ускорение центра масс i-го звена.
Уславливаемся, что центр масс кривошипа лежит на оси его вращения, т.к в большинстве случаев кривошип – вал механизма, т.е ![]()
Также уславливаемся, что у линейных звеньев центр масс лежит на середине звена. Значения ускорений центра масс найдены в кинематическом анализе плоского рычажного механизма. Находим силы инерции:
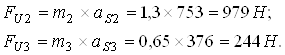 (27)
(27)
Определяем моменты от сил инерции:
![]() (28)
(28)
где ![]() - момент инерции i-го звена, угловое ускорение i-го звена.
- момент инерции i-го звена, угловое ускорение i-го звена.
Момент инерции i-го звена:
![]() (29)
(29)
где ![]() - масса i-го звена,
- масса i-го звена, ![]() - длина i-го звена.
- длина i-го звена.
Находим моменты от сил инерции:
![]()
Момент от сил инерции направлен противоположно направлению действию углового ускорения. Для определения углового ускорения звена необходимо на плане ускорений взять вектор тангенциальной составляющей ускорения звена и мысленно перенести его в ведомую точку звена (точка, стоящая первой в индексе), а ведущую условно остановить. Направление вращения звена при этом будет характеризовать направление углового ускорения звена.
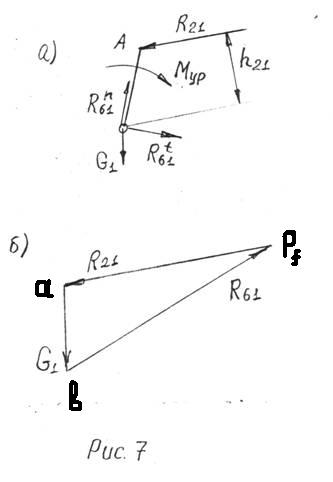
Нанесем на построенное положение механизма все заданные внешние нагрузки. В результате, полученная картина будет являться расчетной схемой данного положения плоского рычажного механизма.
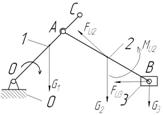
Рисунок 7 – Расчетная схема силового анализа
5. Кинетостатический метод силового анализа
В данном курсовом проекте силовой анализ мы проведем с помощью кинетостатического метода, в основе которого лежит принцип Д’Аламбера. Если к внешним силам, действующим на звенья механизма добавить силы инерции, то данный механизм будет находиться в квазистатическом состоянии. Силовой анализ этого механизма можно выполнить, используя уравнения кинетостатического равновесия:
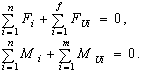 (30)
(30)
Этот метод применяется для анализа движущихся механизмов при известных массах и моментах инерции звеньев.
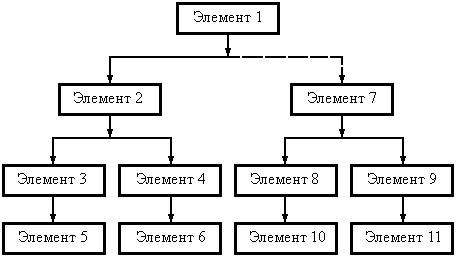
Для этого разбиваем механизм на структурные группы Ассура и начинаем вычерчивать с последней группы звеньев (группы, связанной с выходным звеном).
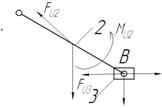
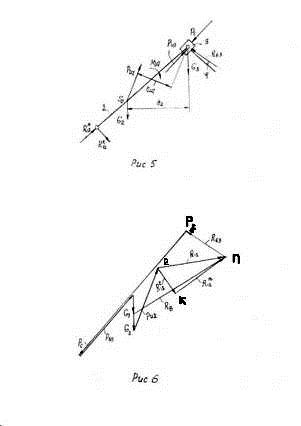
Рисунок 6 – Структурная группа Ассура 1
Разорванную связь 1-2 заменяем реакцией R12, раскладывая ее на составляющие ![]() и
и ![]() , а нормаль XX реакцией R03. Составляем уравнение равновесия:
, а нормаль XX реакцией R03. Составляем уравнение равновесия:
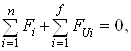 (31)
(31)
![]() (32)
(32)
Уравнение равновесия (32) содержит три неизвестных ![]() ,
, ![]() и
и ![]() , следовательно, его статическая неопределимость равна двум.
, следовательно, его статическая неопределимость равна двум.
С целью раскрытия статической неопределимости найдем модуль![]() .
.
Звено АВ: ![]()
![]() (33)
(33)
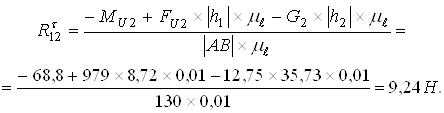
В результате проведенных вычислений уравнение (32) содержит две неизвестных ![]() и
и ![]() , следовательно статическая неопределимость раскрыта полностью. Уравнение равновесия примет следующий вид:
, следовательно статическая неопределимость раскрыта полностью. Уравнение равновесия примет следующий вид:
![]() (34)
(34)
Определение оставшихся неизвестных выполним с помощью плана сил. Для этого необходимо выбрать масштабный коэффициент плана сил:
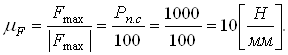 (35)
(35)
Переведем в масштабный коэффициент ![]() оставшиеся силы:
оставшиеся силы:
 (36)
(36)
По полученным величинам строим план сил в масштабном коэффициенте ![]() (рисунок 7).
(рисунок 7).
По построенному плану сил определяем неизвестные ![]() ,
,![]() и
и ![]() :
:
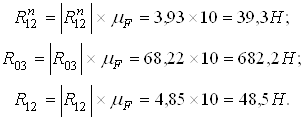 (37)
(37)
Рассмотрим первичный механизм.
Направляем уравновешивающую силу перпендикулярно оси кривошипа, в противоположную сторону вращения оси кривошипа. Вектор выходит из подвижной точки кривошипа.
Составляем уравнение равновесия:
![]() (38)
(38)
Составляем уравнение моментов сил относительно точки O:
![]() (39)
(39)
Из уравнения (4.23) определяем ![]() :
:
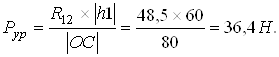
Уравнение равновесия примем следующий вид:
![]() (4.24)
(4.24)
Определим оставшиеся неизвестные с помощью плана сил. Для этого необходимо выбрать масштабный коэффициент сил:

Переведем в масштабный коэффициент оставшиеся силы:
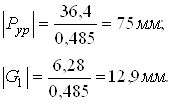
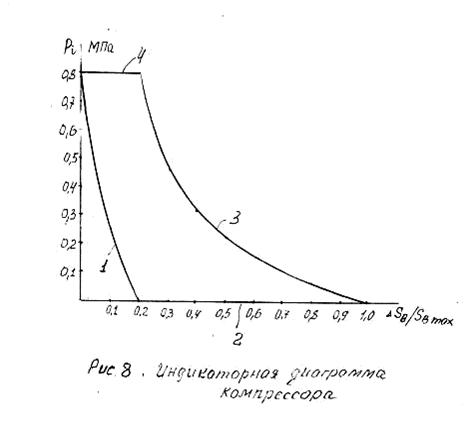
По полученным данным строим план сил в масштабном коэффициенте![]() (рисунок 8).
(рисунок 8).
По построенному плану определяем неизвестную реакцию ![]() :
:
![]()
Метод кинетостатики силового анализа завершен.
Похожие работы
... б) с точечным формообразующим контактом 1 2 силовое 5 Плоская а) обычная б) с пальцем 3 2 Силовое Силовое и геометрическое 4. СТРУКТУРНЫЕ СВОЙСТВА МЕХАНИЗМОВ 4.1. Сложность N механизма. В металлорежущих станках сложные подвижные механические системы, передающие движения от входного звена к выходному (шпиндель, суппорт и ...
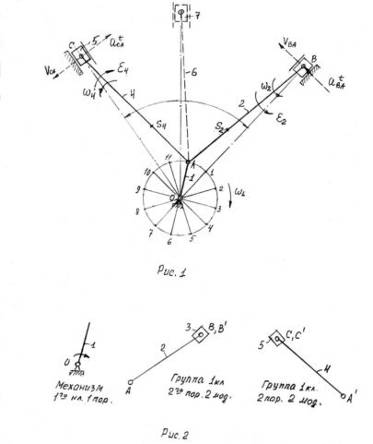
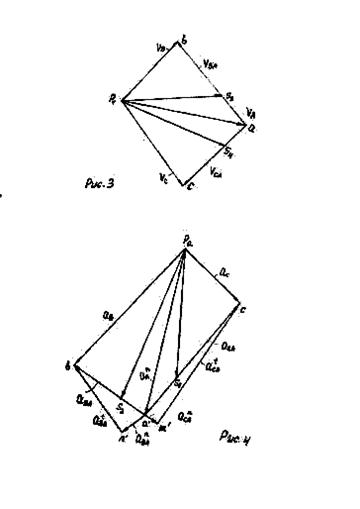
... отрезка "ав". Соединив точки S2 и S4 с полюсом плана скоростей получим векторы скоростей этих точек, а величина скоростей определится из соотношений: . Построенный план скоростей для механизма компрессора позволяет определить угловые скорости звеньев 2 и 4 в их вращательном движении. Как уже говорилось, отрезок плана скоростей ав (вектор) обозначает скорость точки "В" относительно точки ...
... обеспечивающим выполнение технологического процесса сшивания материалов и входящим в число исходных данных для выполнения прочностных расчетов игл. Угол заточки иглы . Общая длина лезвия иглы от острия до колбы: l1=L-(l2+l3) мм (1.1) L – общая длина иглы: в универсальных швейных машинах L=38 мм l2 – длина колбы, выступающая из игловодителя: в зависимости от лапки принимает- ся ...
... , , . Произведем оценку числа возможных вариантов, которые можно синтезировать на основе морфологической матрицы при наложении на нее граничных условий проектирования, а именно исключения вышеперечисленных вариантов: Для всего PC машины поточной линии прядильного производства оценка полных решений может быть проведена по следующей формуле: , где – количество исполнительных механизмов в ...
0 комментариев