Статика корабля

 

ТЕМА: РАСЧЕТЫ ПО СТАТИКЕ КОРАБЛЯ

ОГЛАВЛЕНИЕ

Введение

1. Исходные данные

2. Кривые элементов теоретического чертежа

3. Масштаб Бонжана

4. Расчет посадки и остойчивости судна

5. Расчет посадки и остойчивости поврежденного судна

6. Сводные данные

7. Проверка по критерию погоды и ускорения

Заключение.

Приложение 1. Масштаб Бонжана

Приложение 2.Строеввя по шпангоутам

Приложение 3. Диаграмма статической и динамической остойчивости

Список литературы

ВВЕДЕНИЕ

Задача судостроительных наук — изучение отдельных эксплуатационных и мореходных качеств судна, а также техники, обеспечивающей эти качества. Одной из наиболее важных судостроительных наук является теория корабля (или теория судна).

Теорией корабля называется наука о равновесии и движении судна. Она состоит из двух частей — статики судна и динамики судна.

Под статикой корабля обычно подразумевают раздел теории корабля, посвященный изучению основных мореходных качеств — плавучести и остойчивости целого и поврежденного корабля.

Задача статики состоит:

1) в установлении характеристик, при помощи которых можно оценить качественно и количественно плавучесть и остойчивость целого и поврежденного корабля;

2) в установлении математической связи между размерами и формой корабля и характеристиками плавучести и остойчивости;

3) в разработке практических методов расчета, позволяющих вычислить характеристики плавучести и остойчивости исходя из размеров и формы обводов корабля.

Размеры и форма обводов корабля фиксируются на теоретическом чертеже, который является основным чертежом всякого судна. Так как обводы корабля задаются только теоретическим чертежом и не выражаются аналитическими зависимостями, необходимые для определения характеристик плавучести и остойчивости расчеты выполняют исходя из размеров, снятых с теоретического чертежа, и применяя известные в математике методы приближенного вычисления определенных интегралов.

Исходя из вышесказанного можно сформулировать цель данной работы:

-  Создание плазовой таблицы судна путем ее пересчета с плазовой таблицы судна-прототипа.

-  Создание теоретического чертежа.

-  Расчеты кривых элементов теоретического чертежа, масштаба Бонжана, посадки и остойчивости для судна в полном грузу.

-  Создание повреждения судна и расчет элементов поврежденного судна.

Расчеты в данной работе выполнены с помощью программы S1, созданной в С-Пб. ГМТУ.

Программа S1 предназначена для проведения ряда гидростатических расчетов морских транспортных судов в рамках курсовых и дипломных проектов.

Программа S1 позволяет выполнять:

-  ввод теоретического чертежа (по шпангоутам и фор-/ахтерштевня) в графическом редакторе;

-  проверку строевой по шпангоутам, ватерлинии и основных элементов судна-проекта;

-  линейное (афинноe) перестроение теоретического чертежа при изменении длины, ширины, и/или осадки или увеличение цилиндрической вставки;

-  ввод 5-ти вариантов нагрузки судна;

-  расчет кривых элементов теоретического чертежа;

-  расчет Масштаба Бонжана и Кривых Власова;

-  удифферентовка (расчет посадки) судна;

-  расчет остойчивости судна на больших углах крена (диаграмма остойчивости);

-  расчет изгибающих моментов и перерезывающих сил на тихой воде;

-  вывод результатов в виде отчетных таблиц и графиков на экране и в файл формата DXF;

-  вывод теоретического чертежа в текстовый файл;

-  вывод теоретического чертежа в файл типа DXF для использования в чертежных программах, таких как AutoCAD (как в двухмерном, так и в трехмерном описании);

-  расчет непотопляемости судна по специальной методике.

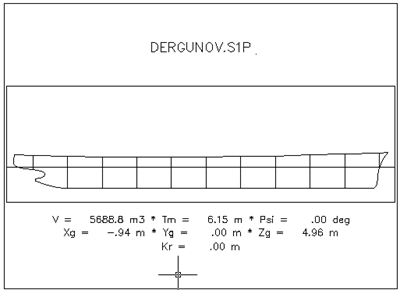
Рисунок 1. Пример DXF файла, созданного программой S1

В ходе выполнения данной работы необходимо построить теоретический чертеж корпуса судна. Для построения корпуса и контуров штевней составляем таблицу основных абсцисс, ординат и аппликат. В исходной таблице даны значения безразмерных абсцисс, ординат и аппликат корпуса судна.

При составлении таблиц использованы следующие обозначения:

ВП - ординаты линии борта главной палубы;

Zвп - аппликаты линии борта главной палубы;

Z1 - аппликаты контуров» шпангоутов на первом батоксе;

Z2 - аппликаты контуров шпангоутов на втором батоксе;

Zф - аппликата точки пересечения контура форштевня с верхней палубой;

Zа - аппликата точки пересечения контура ахтервтевня с верхней палубой;

Xф - абсциссы контура форштевня, отсчитываемые от нулевого шпангоута: положительные в нос, отрицательные в корму;

Xа - абсциссы контура ахтерштевня, отсчитываемые от десятого шпангоута: положительные в нос, отрицательные в корму.

Затем составляем таблицу, аналогичную приведенной в задании, но содержащую размерные величины абсцисс, ординат и аппликат. По данным заполненной таблицы строим теоретический чертеж корпуса судна.

1.  ИСХОДНЫЕ ДАННЫЕ

Длина между перпендикулярами:					Lpp=	100	м
Отношение длины к ширине:					L/B=	6.5
Отношение ширины к осадке:					B/T=	2.5
Исходная безразмерная таблица плазовых ординат. Таблица 1.1
№ ВЛ	Ординаты											Xф	Xа
	Номера теоретических шпангоутов
	0	1	2	3	4	5	6	7	8	9	10
0	-	0.000	0.096	0.358	0.585	0.699	0.513	0.348	0.165	0.009	-	-0.190	0.893
1	-	0.173	0.414	0.707	0.912	0.968	0.868	0.651	0.379	0.183	-	-0.089	0.417
2	-	0.204	0.498	0.800	0.969	1.000	0.958	0.783	0.450	0.226	-	-0.065	0.083
3	-	0.215	0.540	0.837	0.978	1.000	0.995	0.863	0.536	0.222	-	-0.052	0.208
4	-	0.220	0.559	0.849	0.985	1.000	1.000	0.915	0.650	0.240	-	-0.038	0.346
5	-	0.231	0.578	0.859	0.986	1.000	1.000	0.952	0.789	0.433	-	-0.024	0.226
6ГВЛ	0.000	0.252	0.604	0.870	0.987	1.000	1.000	0.975	0.885	0.610	0.225	0.000	-0.426
7	0.016	0.293	0.645	0.886	0.987	1.000	1.000	0.991	0.945	0.737	0.369	0.031	-0.548
8	0.041	0.363	0.697	0.903	0.987	1.000	1.000	1.000	0.971	0.819	0.463	0.083	-0.558
ВП	0.149	0.544	0.797	0.930	0.987	1.000	1.000	1.000	0.986	0.873	0.548	0.247	-0.536
Zвп	1.677	1.633	1.583	1.533	1.510	1.490	1.479	1.479	1.481	1.510	1.563	Zф	Zа
Z1	-	1.275	0.090	0.000	0.000	0.000	0.000	0.000	0.106	0.760	1.123
Z2	-	-	1.250	0.138	0.013	0.000	0.030	0.185	0.685	1.073	-	1.688	1.594
Главные размерения судна:
Длина наибольшая:					Lmax=	107.83	м
Длина между перпендикулярами:					Lpp=	100.00	м
Ширина:					B=	15.38	м
Высота борта на миделе:					H=	9.17	м
Осадка судна:					T=	7.69	м
Теоретическая шпация:					dL=	10	м
Таблица плазовых ординат судна.												Таблица 2
№ ВЛ	Ординаты, м											Xф от миделя, м	Xа от миделя, м
	Номера теоретических шпангоутов
	0	1	2	3	4	5	6	7	8	9	10
0	-	0.00	0.74	2.75	4.50	5.38	3.94	2.68	1.27	0.07	-	48.10	-41.07
1	-	1.33	3.18	5.44	7.01	7.44	6.67	5.01	2.91	1.41	-	49.11	-45.83
2	-	1.57	3.83	6.15	7.45	7.69	7.37	6.02	3.46	1.74	-	49.35	-49.17
3	-	1.65	4.15	6.44	7.52	7.69	7.65	6.64	4.12	1.71	-	49.48	-47.92
4	-	1.69	4.30	6.53	7.57	7.69	7.69	7.04	5.00	1.85	-	49.62	-46.54
5	-	1.78	4.44	6.61	7.58	7.69	7.69	7.32	6.07	3.33	-	49.76	-47.74
6ГВЛ	0.00	1.94	4.64	6.69	7.59	7.69	7.69	7.50	6.81	4.69	1.73	50.00	-54.26
7	0.12	2.26	4.96	6.81	7.59	7.69	7.69	7.62	7.27	5.67	2.84	50.31	-55.48
8	0.32	2.79	5.36	6.94	7.59	7.69	7.69	7.69	7.47	6.30	3.56	50.83	-55.58
ВП	1.15	4.18	6.13	7.15	7.59	7.69	7.69	7.69	7.58	6.71	4.21	52.47	-55.36
Zвп, м	10.31	10.05	9.74	9.43	9.29	9.16	9.10	9.10	9.11	9.29	9.61	Zф от ОП, м	Zа, от ОП, м
Z1, м	-	7.85	0.55	0.00	0.00	0.00	0.00	0.00	0.65	4.67	6.91
Z2, м	-	-	7.69	0.85	0.08	0.00	0.18	1.14	4.21	6.60	-	10.38	9.80

По данным приведенной выше пересчитанной плазовой таблицы в программе “S1” создана математическая модель корпуса судна.

Рис. 1.2 Проекция корпус теоретического чертежа корпуса судна

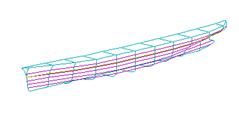
Рис. 1.3 Трехмерная математическая модель корпуса судна

Далее приведены результаты расчетов в табличной форме, выполненные с помощью программы “S1”.

2.  КРИВЫЕ ЭЛЕМЕНТОВ ТЕОРЕТИЧЕСКОГО ЧЕРТЕЖА

Кривые элементов теоретического чертежа – это группа величин, вычисляемых с использованием геометрической модели судна.

К кривым элементов теоретического чертежа относят:

-  Объемное водоизмещение V:

 

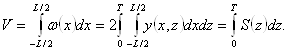
где w(х) – площадь погруженной части теоретического шпангоута с абсциссой х;

у(x,z) – ордината точки на теоретической поверхности корпуса, симметричного относительно ДП;

S(z) – площадь теоретической ватерлинии, параллельно ОП.

-  Координаты центра величины x_c и z_c (у_с=0 в силу симметрии корпуса судна относительно ДП):

 

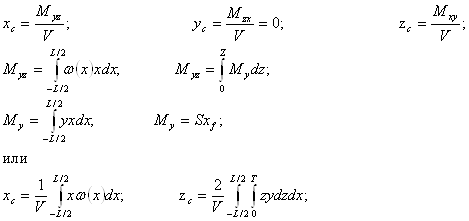
где Му – статический момент площади ватерлинии относительно оси OY;

Xf – абсцисса центра тяжести площади действующей ватерлинии;

Mxy, Myz, Mzx – статические моменты водоизмещения относительно осей OZ, OX, OY соответственно.

-  Площадь ватерлинии S:

 

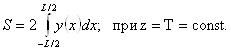
-  Абсцисса центра тяжести площади ватерлинии x_f:

 

 

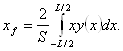
-  Центральные моменты инерции площади ватерлинии Ix и Iyf;

 

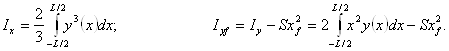
-  Продольный (R) и поперечный (r) метацентрические радиусы:

 

-  Аппликата поперечного метацентра:

 

-  Коэффициенты полноты.

В данном разделе приведены результаты расчетов кривых элементов теоретического чертежа судна.

программа S1 - DERGUNOV.KET Таблица 2.1

╔════════════════════════════════════════════════════════════╗

║ расчет кривой элементов теоретического чертежа ║

╠════════════════════════════════════════════════════════════╣

║ T - осадка, м ║

║ V - обьёмное водоизмещение, м**3 ║

║ Xc - координаты центра величины, м ║

║ Zc - координаты центра величины, м ║

║ r - поперечный метацентрический радиус, м ║

║ R - продольный метацентрический радиус, м ║

║ Zm - параметр Zm=(4)+(5),м ║

╠═══════╤══════════╤════════╤═══════╤═══════╤═══════╤════════╣

║ T │ V │ Xc │ Zc │ r │ R │ Zm ║

╟───────┼──────────┼────────┼───────┼───────┼───────┼────────╢

║ .10 │ 33.8 │ 5.00 │ .05 │ 112.7 │ 4793. │ 112.73 ║

║ .56 │ 318.1 │ .33 │ .30 │ 22.3 │ 869. │ 22.56 ║

║ 1.02 │ 660.4 │ .74 │ .55 │ 14.1 │ 505. │ 14.63 ║

║ 1.48 │ 1043.9 │ .51 │ .80 │ 10.4 │ 354. │ 11.18 ║

║ 1.93 │ 1445.3 │ .52 │ 1.05 │ 8.2 │ 273. │ 9.27 ║

║ 2.39 │ 1862.2 │ .19 │ 1.30 │ 6.8 │ 220. │ 8.11 ║

║ 2.85 │ 2295.6 │ .25 │ 1.54 │ 5.8 │ 183. │ 7.33 ║

║ 3.31 │ 2726.8 │ .18 │ 1.78 │ 5.0 │ 156. │ 6.83 ║

║ 3.77 │ 3175.9 │ .10 │ 2.03 │ 4.5 │ 137. │ 6.51 ║

║ 4.23 │ 3614.6 │ .09 │ 2.27 │ 4.1 │ 124. │ 6.33 ║

║ 4.68 │ 4076.9 │ -.03 │ 2.52 │ 3.7 │ 115. │ 6.25 ║

║ 5.14 │ 4551.8 │ -.23 │ 2.76 │ 3.5 │ 111. │ 6.25 ║

║ 5.60 │ 5035.1 │ -.53 │ 3.02 │ 3.3 │ 111. │ 6.30 ║

║ 6.06 │ 5540.1 │ -.82 │ 3.27 │ 3.1 │ 110. │ 6.38 ║

║ 6.52 │ 6064.8 │ -1.19 │ 3.54 │ 2.9 │ 108. │ 6.48 ║

║ 6.98 │ 6604.5 │ -1.52 │ 3.80 │ 2.8 │ 105. │ 6.60 ║

║ 7.44 │ 7145.8 │ -1.84 │ 4.06 │ 2.7 │ 103. │ 6.73 ║

║ 7.89 │ 7706.8 │ -2.09 │ 4.32 │ 2.6 │ 100. │ 6.88 ║

║ 8.35 │ 8272.6 │ -2.29 │ 4.59 │ 2.4 │ 97. │ 7.03 ║

║ 8.81 │ 8856.6 │ -2.50 │ 4.85 │ 2.3 │ 95. │ 7.19 ║

╚═══════╧══════════╧════════╧═══════╧═══════╧═══════╧════════╝

Таблица 2.2

╔════════════════════════════════════════════════════════════╗

║ расчет кривой элементов теоретического чертежа ║

╠════════════════════════════════════════════════════════════╣

║ T - осадка, м ║

║ S - площадь ватерлинии, м**2 ║

║ Xf - координаты ЦТ площади ватерлинии, м ║

║ моменты инерции площади ватерлинии : ║

║ Ix - относительно центральной продольной оси, м**4 ║

║ Iy - относительно оси Y через мидель, м**4 ║

║ If - относительно центральнoй поперечной оси, м**4 ║

╠═══════╤══════════╤════════╤══════════╤══════════╤══════════╣

║ T │ S │ Xf │ Ix │ Iy │ If ║

╟───────┼──────────┼────────┼──────────┼──────────┼──────────╢

║ .10 │ 521.5 │ .11 │ .381E+04 │ .162E+06 │ .162E+06 ║

║ .56 │ 707.2 │ .81 │ .708E+04 │ .277E+06 │ .276E+06 ║

║ 1.02 │ 799.3 │ .70 │ .930E+04 │ .334E+06 │ .333E+06 ║

║ 1.48 │ 855.8 │ .49 │ .108E+05 │ .369E+06 │ .369E+06 ║

║ 1.93 │ 893.3 │ .25 │ .119E+05 │ .394E+06 │ .394E+06 ║

║ 2.39 │ 920.0 │ .07 │ .127E+05 │ .410E+06 │ .410E+06 ║

║ 2.85 │ 939.3 │ -.04 │ .133E+05 │ .421E+06 │ .421E+06 ║

║ 3.31 │ 952.7 │ -.09 │ .138E+05 │ .427E+06 │ .427E+06 ║

║ 3.77 │ 967.5 │ -.30 │ .142E+05 │ .435E+06 │ .435E+06 ║

║ 4.23 │ 985.1 │ -.64 │ .147E+05 │ .448E+06 │ .447E+06 ║

║ 4.68 │ 1008.8 │ -1.20 │ .152E+05 │ .469E+06 │ .467E+06 ║

║ 5.14 │ 1043.7 │ -2.14 │ .159E+05 │ .505E+06 │ .500E+06 ║

║ 5.60 │ 1086.0 │ -3.36 │ .165E+05 │ .559E+06 │ .547E+06 ║

║ 6.06 │ 1122.5 │ -4.29 │ .172E+05 │ .610E+06 │ .589E+06 ║

║ 6.52 │ 1154.8 │ -4.91 │ .178E+05 │ .655E+06 │ .627E+06 ║

║ 6.98 │ 1184.1 │ -5.31 │ .185E+05 │ .697E+06 │ .663E+06 ║

║ 7.44 │ 1209.6 │ -5.50 │ .191E+05 │ .734E+06 │ .697E+06 ║

║ 7.89 │ 1233.2 │ -5.55 │ .197E+05 │ .769E+06 │ .731E+06 ║

║ 8.35 │ 1256.0 │ -5.48 │ .202E+05 │ .805E+06 │ .767E+06 ║

║ 8.81 │ 1278.0 │ -5.30 │ .208E+05 │ .840E+06 │ .804E+06 ║

╚═══════╧══════════╧════════╧══════════╧══════════╧══════════╝

Таблица 2.3

╔════════════════════════════════════════════════════════════╗

║ расчет кривой элементов теоретического чертежа ║

╠════════════════════════════════════════════════════════════╣

║ T - осадка, м ║

║ V - обьёмное водоизмещение, м**3 ║

║ Lwl - длина ватерлинии, м ║

║ Для расчета управляемости судна: ║

║ Sн - площадь носового подреза отн. Lwl, м**2 ║

║ Sк - площадь кормового подреза отн. Lwl, м**2 ║

║ Для расчета сопротивления воды движения судна: ║

║ SF - плошадь смоченной поверхности, м**2 ║

╠═══════╤══════════╤════════╤══════════╤══════════╤══════════╣

║ T │ V │ Lwl │ Sн │ Sк │ SF ║

╟───────┼──────────┼────────┼──────────┼──────────┼──────────╢

║ .10 │ 33.8 │ 89.92 │ .01 │ .02 │ 523.5 ║

║ .56 │ 318.1 │ 92.53 │ .15 │ .15 │ 728.3 ║

║ 1.02 │ 660.4 │ 94.88 │ .33 │ 1.10 │ 853.5 ║

║ 1.48 │ 1043.9 │ 96.57 │ .49 │ .94 │ 956.3 ║

║ 1.93 │ 1445.3 │ 98.13 │ .64 │ 1.89 │ 1050.4 ║

║ 2.39 │ 1862.2 │ 98.56 │ .79 │ 2.24 │ 1139.5 ║

║ 2.85 │ 2295.6 │ 98.39 │ .94 │ 1.76 │ 1226.0 ║

║ 3.31 │ 2726.8 │ 96.89 │ 1.13 │ -2.12 │ 1311.8 ║

║ 3.77 │ 3175.9 │ 96.25 │ 1.34 │ -4.21 │ 1397.9 ║

║ 4.23 │ 3614.6 │ 96.22 │ 1.58 │ -4.54 │ 1484.8 ║

║ 4.68 │ 4076.9 │ 96.54 │ 1.93 │ -3.38 │ 1576.0 ║

║ 5.14 │ 4551.8 │ 97.65 │ 2.27 │ 2.58 │ 1675.0 ║

║ 5.60 │ 5035.1 │ 101.05 │ 2.81 │ 24.13 │ 1843.7 ║

║ 6.06 │ 5540.1 │ 103.83 │ 3.39 │ 43.37 │ 1964.0 ║

║ 6.52 │ 6064.8 │ 105.00 │ 4.08 │ 51.73 │ 2137.3 ║

║ 6.98 │ 6604.5 │ 105.54 │ 5.09 │ 55.03 │ 2244.0 ║

║ 7.44 │ 7145.8 │ 105.92 │ 6.39 │ 56.80 │ 2347.5 ║

║ 7.89 │ 7706.8 │ 106.19 │ 8.15 │ 57.17 │ 2449.7 ║

║ 8.35 │ 8272.6 │ 106.47 │ 10.34 │ 57.25 │ 2551.9 ║

║ 8.81 │ 8856.6 │ 106.71 │ 12.91 │ 56.65 │ 2654.2 ║

╚═══════╧══════════╧════════╧══════════╧══════════╧══════════╝

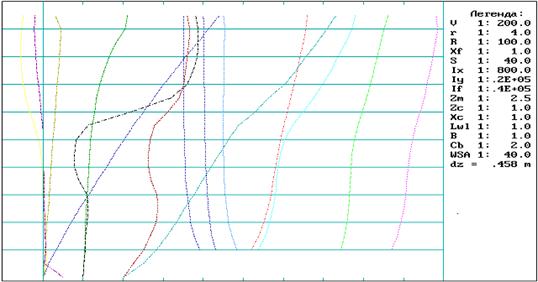
Рис. 2.1 Кривые элементов теоретического чертежа

3.  МАСШТАБ БОНЖАНА

Масштаб Бонжана представляет собой совокупность кривых, каждая из которых определяет погруженную площадь шпангоута в зависимости от его углубления и строится от следа соответствующего шпангоута на диаметральной плоскости судна. Чтобы использовать масштаб Бонжана, прежде всего, наносим на него ватерлинию судна. После нанесения ватерлинии в точках ее пересечения со следами шпангоутов снимаем с кривых значения погруженных площадей шпангоутов и вычисляем водоизмещение и абсциссу центра величины.

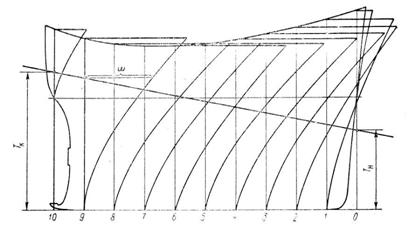
Рис. 3.1 Пример построения масштаба Бонжана

С помощью масштаба Бонжана строим строевую по шпангоутам, которая используется в расчетах общей продольной прочности судна, также при разработке теоретического чертежа. Строевая по шпангоутам представляет собой кривую, ординаты которой в некотором выбранном масштабе равны погруженным по заданную ватерлинию WL площадям шпангоутов, отложенным вдоль следов шпангоутов на диаметральной плоскости судна. Таким образом, эта кривая характеризует закон распределения погруженных площадей шпангоутов по длине судна.

Кривыми Власова называют кривые статических моментов половины площади шпангоута относительно осей OZ и OY.

Площадь шпангоута:

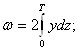
Половина площади шпангоута:

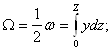
Статические моменты половины площади шпангоута относительно осей OZ и OY соответственно:

В данном разделе приведены результаты расчетов масштаба Бонжана математической модели корпуса судна.

программа S1 - DERGUNOV.KWT Таблица 3.1

╔════════════════════════════════════════════════════════════╗

║ расчет масштаба Бонжана и кривых В.Г. Власова ║

╠════════════════════════════════════════════════════════════╣

║ шпангоут номер : 1 X = 50.00 м ║

╠════════════════════════════════════════════════════════════╣

║ (T) - осадка, м ║

║ (O) - площадь шпангоута, м**2 ║

║ (B) - статический момент относительно ОY, м**3 ║

║ (C) - статический момент относительно ОZ, м**3  ║

║ (Z) - аппликата центра площади шпангоута, м ║

╠════════╤═══════════╤══════════════╤═════════════╤══════════╣

║ (T) │ (O) │ (B) │ (C) │ (Z) ║

╟────────┼───────────┼──────────────┼─────────────┼──────────╢

║ 11.00 │ 3.4 │ .6 │ 15.4 │ 9.16 ║

║ 10.45 │ 3.4 │ .6 │ 15.4 │ 9.16 ║

║ 9.90 │ 2.5 │ .3 │ 11.1 │ 8.85 ║

║ 9.35 │ 1.6 │ .2 │ 6.9 │ 8.43 ║

║ 8.80 │ 1.0 │ .1 │ 4.1 │ 8.03 ║

║ 8.25 │ .6 │ .0 │ 2.2 │ 7.63 ║

║ 7.70 │ .3 │ .0 │ 1.0 │ 7.23 ║

║ 7.15 │ .1 │ .0 │ .3 │ 6.84 ║

║ 6.60 │ .0 │ .0 │ .0 │ 6.45 ║

║ 6.05 │ -- │ -- │ -- │ -- ║

║ 5.50 │ -- │ -- │ -- │ -- ║

║ 4.95 │ -- │ -- │ -- │ -- ║

║ 4.40 │ -- │ -- │ -- │ -- ║

║ 3.85 │ -- │ -- │ -- │ -- ║

║ 3.30 │ -- │ -- │ -- │ -- ║

║ 2.75 │ -- │ -- │ -- │ -- ║

║ 2.20 │ -- │ -- │ -- │ -- ║

║ 1.65 │ -- │ -- │ -- │ -- ║

║ 1.10 │ -- │ -- │ -- │ -- ║

║ .55 │ -- │ -- │ -- │ -- ║

╚════════╧═══════════╧══════════════╧═════════════╧══════════╝

Таблица 3.1 (продолжение)

╔════════════════════════════════════════════════════════════╗

║ расчет масштаба Бонжана и кривых В.Г. Власова ║

╠════════════════════════════════════════════════════════════╣

║ шпангоут номер : 2 X = 40.00 м ║

╠════════════════════════════════════════════════════════════╣

║ (T) - осадка, м ║

║ (O) - площадь шпангоута, м**2  ║

║ (B) - статический момент относительно ОY, м**3 ║

║ (C) - статический момент относительно ОZ, м**3 ║

║ (Z) - аппликата центра площади шпангоута, м ║

╠════════╤═══════════╤══════════════╤═════════════╤══════════╣

║ (T) │ (O) │ (B) │ (C) │ (Z) ║

╟────────┼───────────┼──────────────┼─────────────┼──────────╢

║ 11.00 │ 41.1 │ 24.3 │ 125.2 │ 6.09 ║

║ 10.45 │ 41.1 │ 24.3 │ 125.2 │ 6.09 ║

║ 9.90 │ 39.7 │ 22.7 │ 118.0 │ 5.95 ║

║ 9.35 │ 35.5 │ 18.7 │ 97.7 │ 5.51 ║

║ 8.80 │ 32.0 │ 15.9 │ 81.8 │ 5.12 ║

║ 8.25 │ 28.6 │ 13.4 │ 67.7 │ 4.73 ║

║ 7.70 │ 25.7 │ 11.4 │ 55.9 │ 4.35 ║

║ 7.15 │ 23.1 │ 9.8 │ 46.1 │ 4.00 ║

║ 6.60 │ 20.6 │ 8.5 │ 37.8 │ 3.66 ║

║ 6.05 │ 18.5 │ 7.5 │ 31.0 │ 3.36 ║

║ 5.50 │ 16.4 │ 6.5 │ 25.1 │ 3.05 ║

║ 4.95 │ 14.5 │ 5.6 │ 19.9 │ 2.76 ║

║ 4.40 │ 12.5 │ 4.8 │ 15.5 │ 2.46 ║

║ 3.85 │ 10.7 │ 4.0 │ 11.6 │ 2.17 ║

║ 3.30 │ 8.9 │ 3.2 │ 8.4 │ 1.89 ║

║ 2.75 │ 7.0 │ 2.5 │ 5.6 │ 1.59 ║

║ 2.20 │ 5.3 │ 1.8 │ 3.4 │ 1.30 ║

║ 1.65 │ 3.6 │ 1.1 │ 1.8 │ 1.00 ║

║ 1.10 │ 2.0 │ .5 │ .7 │ .68 ║

║ .55 │ .6 │ .1 │ .1 │ .35 ║

╚════════╧═══════════╧══════════════╧═════════════╧══════════╝

Таблица 3.1 (продолжение)

╔════════════════════════════════════════════════════════════╗

║ расчет масштаба Бонжана и кривых В.Г. Власова ║

╠════════════════════════════════════════════════════════════╣

║ шпангоут номер : 3 X = 30.00 м ║

╠════════════════════════════════════════════════════════════╣

║ (T) - осадка, м ║

║ (O) - площадь шпангоута, м**2 ║

║ (B) - статический момент относительно ОY, м**3 ║

║ (C) - статический момент относительно ОZ, м**3  ║

║ (Z) - аппликата центра площади шпангоута, м ║

╠════════╤═══════════╤══════════════╤═════════════╤══════════╣

║ (T) │ (O) │ (B) │ (C) │ (Z) ║

╟────────┼───────────┼──────────────┼─────────────┼──────────╢

║ 11.00 │ 85.3 │ 98.0 │ 232.9 │ 5.46 ║

║ 10.45 │ 85.3 │ 98.0 │ 232.9 │ 5.46 ║

║ 9.90 │ 85.3 │ 98.0 │ 232.9 │ 5.46 ║

║ 9.35 │ 80.5 │ 90.7 │ 210.1 │ 5.22 ║

║ 8.80 │ 74.1 │ 81.4 │ 181.0 │ 4.88 ║

║ 8.25 │ 68.2 │ 73.5 │ 155.9 │ 4.57 ║

║ 7.70 │ 62.4 │ 65.8 │ 132.7 │ 4.25 ║

║ 7.15 │ 56.8 │ 58.6 │ 111.8 │ 3.94 ║

║  6.60 │ 51.4 │ 52.1 │ 93.5 │ 3.63 ║

║ 6.05 │ 46.3 │ 46.1 │ 77.2 │ 3.34 ║

║ 5.50 │ 41.3 │ 40.4 │ 62.7 │ 3.04 ║

║ 4.95 │ 36.4 │ 34.9 │ 49.9 │ 2.74 ║

║ 4.40 │ 31.5 │ 29.6 │ 38.6 │ 2.45 ║

║ 3.85 │ 26.8 │ 24.5 │ 28.9 │ 2.15 ║

║ 3.30 │ 22.2 │ 19.6 │ 20.6 │ 1.86 ║

║ 2.75 │ 17.6 │ 14.9 │ 13.7 │ 1.55 ║

║ 2.20 │ 13.2 │ 10.6 │ 8.3 │ 1.25 ║

║ 1.65 │ 9.1 │ 6.7 │ 4.3 │ .94 ║

║ 1.10 │ 5.3 │ 3.5 │ 1.7 │ .63 ║

║ .55 │ 2.1 │ 1.1 │ .3 │ .32 ║

╚════════╧═══════════╧══════════════╧═════════════╧══════════╝

Таблица 3.1 (продолжение)

╔════════════════════════════════════════════════════════════╗

║ расчет масштаба Бонжана и кривых В.Г. Власова ║

╠════════════════════════════════════════════════════════════╣

║ шпангоут номер : 4 X = 20.00 м ║

╠════════════════════════════════════════════════════════════╣

║ (T) - осадка, м ║

║ (O) - площадь шпангоута, м**2 ║

║ (B) - статический момент относительно ОY, м**3 ║

║ (C) - статический момент относительно ОZ, м**3 ║

║ (Z) - аппликата центра площади шпангоута, м ║

╠════════╤═══════════╤══════════════╤═════════════╤══════════╣

║ (T) │ (O) │ (B) │ (C) │ (Z) ║

╟────────┼───────────┼──────────────┼─────────────┼──────────╢

║ 11.00 │ 119.8 │ 193.0 │ 298.6 │ 4.99 ║

║ 10.45 │ 119.8 │ 193.0 │ 298.6 │ 4.99 ║

║  9.90 │ 119.8 │ 193.0 │ 298.6 │ 4.99 ║

║ 9.35 │ 118.5 │ 190.7 │ 293.0 │ 4.94 ║

║ 8.80 │ 110.8 │ 177.1 │ 257.9 │ 4.65 ║

║ 8.25 │ 103.1 │ 163.7 │ 225.0 │ 4.37 ║

║ 7.70 │ 95.5 │ 150.4 │ 194.6 │ 4.08 ║

║ 7.15 │ 87.9 │ 137.4 │ 166.6 │ 3.79 ║

║ 6.60 │ 80.5 │ 124.9 │ 141.0 │ 3.50 ║

║ 6.05 │ 73.1 │ 112.5 │ 117.7 │ 3.22 ║

║ 5.50 │ 65.8 │ 100.3 │ 96.6 │ 2.94 ║

║ 4.95 │ 58.5 │ 88.3 │ 77.5 │ 2.65 ║

║ 4.40 │ 51.3 │ 76.4 │ 60.6 │ 2.36 ║

║ 3.85 │ 44.1 │ 64.7 │ 45.8 │ 2.08 ║

║ 3.30 │  37.0 │ 53.1 │ 33.1 │ 1.79 ║

║ 2.75 │ 29.9 │ 41.8 │ 22.4 │ 1.50 ║

║ 2.20 │ 23.0 │ 30.9 │ 13.8 │ 1.20 ║

║ 1.65 │ 16.3 │ 20.7 │ 7.4 │ .91 ║

║ 1.10 │ 9.9 │ 11.5 │ 3.0 │ .60 ║

║ .55 │ 4.2 │ 4.1 │ .6 │ .30 ║

╚════════╧═══════════╧══════════════╧═════════════╧══════════╝

Таблица 3.1 (продолжение)

╔════════════════════════════════════════════════════════════╗

║ расчет масштаба Бонжана и кривых В.Г. Власова ║

╠════════════════════════════════════════════════════════════╣

║ шпангоут номер : 5 X = 10.00 м ║

╠════════════════════════════════════════════════════════════╣

║ (T) - осадка, м ║

║ (O) - площадь шпангоута, м**2 ║

║ (B) - статический момент относительно ОY, м**3 ║

║ (C) - статический момент относительно ОZ, м**3 ║

║ (Z) - аппликата центра площади шпангоута, м ║

╠════════╤═══════════╤══════════════╤═════════════╤══════════╣

║ (T) │ (O) │ (B) │ (C) │ (Z) ║

╟────────┼───────────┼──────────────┼─────────────┼──────────╢

║ 11.00 │ 137.7 │ 255.8 │ 326.1 │ 4.74 ║

║ 10.45 │ 137.7 │ 255.8 │ 326.1 │ 4.74 ║

║ 9.90 │ 137.7 │ 255.8 │ 326.1 │ 4.74 ║

║ 9.35 │ 137.7 │ 255.8 │ 326.1 │ 4.74 ║

║ 8.80 │ 130.3 │ 241.7 │ 292.5 │ 4.49 ║

║ 8.25 │ 121.9 │ 225.8 │ 256.9 │ 4.21 ║

║ 7.70 │ 113.6 │ 210.0 │ 223.6 │ 3.94 ║

║ 7.15 │ 105.2 │ 194.1 │ 192.6 │ 3.66 ║

║ 6.60 │ 96.9 │ 178.3 │ 163.9 │ 3.38 ║

║ 6.05 │ 88.5 │ 162.5 │ 137.5 │ 3.11 ║

║ 5.50 │ 80.2 │ 146.6 │ 113.4 │ 2.83 ║

║ 4.95 │ 71.8 │ 130.8 │ 91.6 │ 2.55 ║

║ 4.40 │  63.5 │ 115.0 │ 72.1 │ 2.27 ║

║ 3.85 │ 55.1 │ 99.2 │ 54.9 │ 1.99 ║

║ 3.30 │ 46.8 │ 83.5 │ 40.1 │ 1.71 ║

║ 2.75 │ 38.6 │ 68.0 │ 27.6 │ 1.43 ║

║ 2.20 │ 30.3 │ 52.6 │ 17.4 │ 1.15 ║

║ 1.65 │ 22.2 │ 37.4 │ 9.5 │ .86 ║

║ 1.10 │ 14.3 │ 23.2 │ 4.1 │ .57 ║

║ .55 │ 6.7 │ 10.3 │ 1.0 │ .28 ║

╚════════╧═══════════╧══════════════╧═════════════╧══════════╝

Таблица 3.1 (продолжение)

╔════════════════════════════════════════════════════════════╗

║ расчет масштаба Бонжана и кривых В.Г. Власова ║

╠════════════════════════════════════════════════════════════╣

║ шпангоут номер : 6 X = .00 м ║

╠════════════════════════════════════════════════════════════╣

║ (T) - осадка, м ║

║ (O) - площадь шпангоута, м**2 ║

║ (B) - статический момент относительно ОY, м**3 ║

║ (C) - статический момент относительно ОZ, м**3 ║

║ (Z) - аппликата центра площади шпангоута, м ║

╠════════╤═══════════╤══════════════╤═════════════╤══════════╣

║ (T) │ (O) │ (B) │ (C) │ (Z) ║

╟────────┼───────────┼──────────────┼─────────────┼──────────╢

║ 11.00 │ 139.1 │ 264.4 │ 322.9 │ 4.64 ║

║ 10.45 │ 139.1 │ 264.4 │ 322.9 │ 4.64 ║

║ 9.90 │ 139.1 │ 264.4 │ 322.9 │ 4.64 ║

║ 9.35 │ 139.1 │ 264.4 │ 322.9 │ 4.64 ║

║ 8.80 │ 133.5 │ 253.4 │ 297.3 │ 4.46 ║

║ 8.25 │ 125.0 │ 237.2 │ 261.3 │ 4.18 ║

║ 7.70 │ 116.5 │ 220.9 │ 227.6 │ 3.91 ║

║ 7.15 │ 108.1 │ 204.6 │ 196.1 │ 3.63 ║

║ 6.60 │ 99.6 │ 188.4 │ 167.1 │ 3.35 ║

║ 6.05 │ 91.2 │ 172.1 │ 140.3 │ 3.08 ║

║ 5.50 │ 82.7 │ 155.9 │ 115.9 │ 2.80 ║

║ 4.95 │ 74.2 │ 139.6 │ 93.8 │ 2.53 ║

║ 4.40 │ 65.8 │ 123.3 │ 74.0 │ 2.25 ║

║ 3.85 │ 57.3 │ 107.1 │ 56.6 │ 1.97 ║

║ 3.30 │ 48.9 │ 90.8 │ 41.5 │ 1.70 ║

║ 2.75 │ 40.4 │ 74.5 │ 28.7 │ 1.42 ║

║ 2.20 │ 31.9 │ 58.3 │ 18.2 │ 1.14 ║

║ 1.65 │ 23.5 │ 42.1 │ 10.1 │ .86 ║

║ 1.10 │ 15.2 │ 26.4 │ 4.3 │ .57 ║

║ .55 │ 7.1 │ 11.6 │ 1.0 │ .28 ║

╚════════╧═══════════╧══════════════╧═════════════╧══════════╝

Таблица 3.1 (продолжение)

╔════════════════════════════════════════════════════════════╗

║ расчет масштаба Бонжана и кривых В.Г. Власова ║

╠════════════════════════════════════════════════════════════╣

║ шпангоут номер : 7 X = -10.00 м ║

╠════════════════════════════════════════════════════════════╣

║ (T) - осадка, м ║

║ (O) - площадь шпангоута, м**2 ║

║ (B) - статический момент относительно ОY, м**3 ║

║ (C) - статический момент относительно ОZ, м**3 ║

║ (Z) - аппликата центра площади шпангоута, м ║

╠════════╤═══════════╤══════════════╤═════════════╤══════════╣

║ (T) │ (O) │ (B) │ (C) │ (Z) ║

╟────────┼───────────┼──────────────┼─────────────┼──────────╢

║ 11.00 │ 134.2 │ 249.7 │ 316.2 │ 4.71 ║

║ 10.45 │ 134.2 │ 249.7 │ 316.2 │ 4.71 ║

║ 9.90 │ 134.2 │ 249.7 │ 316.2 │ 4.71 ║

║ 9.35 │ 134.2 │ 249.7 │ 316.2 │ 4.71 ║

║ 8.80 │ 129.6 │ 240.8 │ 295.6 │ 4.56 ║

║ 8.25 │ 121.2 │ 224.5 │ 259.5 │ 4.28 ║

║ 7.70 │ 112.7 │ 208.3 │ 225.8 │ 4.01 ║

║ 7.15 │ 104.3 │ 192.0 │ 194.4 │ 3.73 ║

║ 6.60 │ 95.8 │ 175.7 │ 165.3 │ 3.45 ║

║ 6.05 │ 87.3 │ 159.5 │ 138.6 │ 3.17 ║

║ 5.50 │ 78.9 │ 143.2 │ 114.1 │ 2.89 ║

║ 4.95 │ 70.4 │ 127.0 │ 92.0 │ 2.61 ║

║ 4.40 │  62.0 │ 110.7 │ 72.3 │ 2.33 ║

║ 3.85 │ 53.5 │ 94.4 │ 54.8 │ 2.05 ║

║ 3.30 │ 45.1 │ 78.3 │ 39.7 │ 1.76 ║

║ 2.75 │ 36.7 │ 62.2 │ 27.0 │ 1.47 ║

║ 2.20 │ 28.4 │ 46.6 │ 16.8 │ 1.18 ║

║ 1.65 │ 20.3 │ 31.9 │ 9.0 │ .89 ║

║ 1.10 │ 12.7 │ 18.5 │ 3.7 │ .59 ║

║ .55 │ 5.6 │ 7.3 │ .8 │ .29 ║

╚════════╧═══════════╧══════════════╧═════════════╧══════════╝

Таблица 3.1 (продолжение)

╔════════════════════════════════════════════════════════════╗

║ расчет масштаба Бонжана и кривых В.Г. Власова ║

╠════════════════════════════════════════════════════════════╣

║ шпангоут номер : 8 X = -20.00 м ║

╠════════════════════════════════════════════════════════════╣

║ (T) - осадка, м ║

║ (O) - площадь шпангоута, м**2 ║

║ (B) - статический момент относительно ОY, м**3 ║

║ (C) - статический момент относительно ОZ, м**3 ║

║ (Z) - аппликата центра площади шпангоута, м ║

╠════════╤═══════════╤══════════════╤═════════════╤══════════╣

║ (T) │ (O) │ (B) │ (C) │ (Z) ║

╟────────┼───────────┼──────────────┼─────────────┼──────────╢

║ 11.00 │ 121.9 │ 210.2 │ 301.9 │ 4.95 ║

║ 10.45 │ 121.9 │ 210.2 │ 301.9 │ 4.95 ║

║ 9.90 │ 121.9 │ 210.2 │ 301.9 │ 4.95 ║

║ 9.35 │ 121.9 │ 210.2 │ 301.9 │ 4.95 ║

║ 8.80 │ 117.3 │ 201.3 │ 281.3 │ 4.80 ║

║ 8.25 │ 108.8 │ 185.0 │ 245.2 │ 4.51 ║

║ 7.70 │ 100.3 │ 168.8 │ 211.5 │ 4.22 ║

║ 7.15 │ 91.9 │ 152.7 │ 180.2 │ 3.92 ║

║ 6.60 │ 83.6 │ 136.9 │ 151.6 │ 3.63 ║

║ 6.05 │ 75.3 │ 121.3 │ 125.4 │ 3.33 ║

║ 5.50 │  67.1 │ 106.1 │ 101.8 │ 3.03 ║

║ 4.95 │ 59.1 │ 91.3 │ 80.7 │ 2.73 ║

║ 4.40 │ 51.1 │ 77.0 │ 62.2 │ 2.43 ║

║ 3.85 │ 43.4 │ 63.4 │ 46.2 │ 2.13 ║

║ 3.30 │ 35.8 │ 50.5 │ 32.7 │ 1.83 ║

║ 2.75 │ 28.6 │ 38.4 │ 21.7 │ 1.52 ║

║ 2.20 │ 21.6 │ 27.4 │ 13.1 │ 1.21 ║

║ 1.65 │ 15.1 │ 17.7 │ 6.8 │ .90 ║

║ 1.10 │ 9.2 │ 9.8 │ 2.7 │ .60 ║

║ .55 │ 4.0 │ 3.6 │ .6 │ .29 ║

╚════════╧═══════════╧══════════════╧═════════════╧══════════╝

Таблица 3.1 (продолжение)

╔════════════════════════════════════════════════════════════╗

║ расчет масштаба Бонжана и кривых В.Г. Власова ║

╠════════════════════════════════════════════════════════════╣

║ шпангоут номер : 9 X = -30.00 м ║

╠════════════════════════════════════════════════════════════╣

║ (T) - осадка, м ║

║ (O) - площадь шпангоута, м**2 ║

║ (B) - статический момент относительно ОY, м**3 ║

║ (C) - статический момент относительно ОZ, м**3 ║

║ (Z) - аппликата центра площади шпангоута, м ║

╠════════╤═══════════╤══════════════╤═════════════╤══════════╣

║ (T) │ (O) │ (B) │ (C) │ (Z) ║

╟────────┼───────────┼──────────────┼─────────────┼──────────╢

║ 11.00 │ 96.4 │ 142.7 │ 262.7 │ 5.45 ║

║ 10.45 │ 96.4 │ 142.7 │ 262.7 │ 5.45 ║

║ 9.90 │ 96.4 │ 142.7 │ 262.7 │ 5.45 ║

║ 9.35 │ 96.4 │ 142.7 │ 262.7 │ 5.45 ║

║ 8.80 │  91.7 │ 133.7 │ 241.5 │ 5.27 ║

║ 8.25 │ 83.5 │ 118.3 │ 206.5 │ 4.95 ║

║ 7.70 │ 75.3 │ 103.1 │ 173.9 │ 4.62 ║

║ 7.15 │ 67.1 │ 88.0 │ 143.6 │ 4.28 ║

║ 6.60 │ 59.2 │ 73.9 │ 116.5 │ 3.93 ║

║ 6.05 │ 51.7 │ 61.0 │ 92.7 │ 3.59 ║

║ 5.50 │ 44.4 │ 48.9 │ 71.7 │ 3.23 ║

║ 4.95 │ 37.8 │ 38.9 │ 54.3 │ 2.88 ║

║ 4.40 │ 31.6 │ 30.2 │ 39.8 │ 2.52 ║

║ 3.85 │ 26.0 │ 23.1 │ 28.3 │ 2.18 ║

║ 3.30 │ 21.0 │ 17.5 │ 19.4 │ 1.85 ║

║ 2.75 │ 16.5 │ 12.9 │ 12.6 │ 1.53 ║

║ 2.20 │ 12.5 │ 9.1 │ 7.6 │ 1.21 ║

║ 1.65 │ 8.7 │ 6.0 │ 4.0 │ .91 ║

║ 1.10 │ 5.3 │ 3.3 │ 1.6 │ .60 ║

║ .55 │ 2.3 │ 1.2 │ .3 │ .30 ║

╚════════╧═══════════╧══════════════╧═════════════╧══════════╝

Таблица 3.1 (продолжение)

╔════════════════════════════════════════════════════════════╗

║ расчет масштаба Бонжана и кривых В.Г. Власова ║

╠════════════════════════════════════════════════════════════╣

║ шпангоут номер : 10 X = -40.00 м ║

╠════════════════════════════════════════════════════════════╣

║ (T) - осадка, м ║

║ (O) - площадь шпангоута, м**2 ║

║ (B) - статический момент относительно ОY, м**3 ║

║ (C) - статический момент относительно ОZ, м**3 ║

║ (Z) - аппликата центра площади шпангоута, м ║

╠════════╤═══════════╤══════════════╤═════════════╤══════════╣

║ (T) │  (O) │ (B) │ (C) │ (Z) ║

╟────────┼───────────┼──────────────┼─────────────┼──────────╢

║ 11.00 │ 62.8 │ 72.2 │ 194.4 │ 6.19 ║

║ 10.45 │ 62.8 │ 72.2 │ 194.4 │ 6.19 ║

║ 9.90 │ 62.8 │ 72.2 │ 194.4 │ 6.19 ║

║ 9.35 │ 62.8 │ 72.2 │ 194.4 │ 6.19 ║

║ 8.80 │ 56.2 │ 61.0 │ 164.4 │ 5.85 ║

║ 8.25 │ 49.3 │ 50.0 │ 134.9 │ 5.47 ║

║ 7.70 │ 42.3 │ 39.1 │ 107.2 │ 5.06 ║

║ 7.15 │ 35.8 │ 29.6 │ 83.1 │ 4.64 ║

║ 6.60 │ 30.1 │ 22.2 │ 63.5 │ 4.22 ║

║ 6.05 │ 24.8 │ 15.6 │ 46.5 │ 3.76 ║

║ 5.50 │  19.9 │ 10.3 │ 32.5 │ 3.27 ║

║ 4.95 │ 16.2 │ 7.1 │ 22.7 │ 2.81 ║

║ 4.40 │ 13.5 │ 5.5 │ 16.5 │ 2.45 ║

║ 3.85 │ 11.5 │ 4.6 │ 12.3 │ 2.15 ║

║ 3.30 │ 9.6 │ 3.7 │ 9.0 │ 1.87 ║

║ 2.75 │ 7.7 │ 2.9 │ 6.1 │ 1.58 ║

║ 2.20 │ 5.8 │ 2.1 │ 3.7 │ 1.29 ║

║ 1.65 │ 3.9 │ 1.3 │ 1.9 │ .98 ║

║ 1.10 │ 2.2 │ .6 │ .7 │ .66 ║

║ .55 │ .8 │ .2 │ .1 │ .34 ║

╚════════╧═══════════╧══════════════╧═════════════╧══════════╝

Таблица 3.1 (продолжение)

╔════════════════════════════════════════════════════════════╗

║ расчет масштаба Бонжана и кривых В.Г. Власова ║

╠════════════════════════════════════════════════════════════╣

║ шпангоут номер : 11 X = -50.00 м ║

╠════════════════════════════════════════════════════════════╣

║ (T) - осадка, м ║

║ (O) - площадь шпангоута, м**2 ║

║ (B) - статический момент относительно ОY, м**3 ║

║ (C) - статический момент относительно ОZ, м**3 ║

║ (Z) - аппликата центра площади шпангоута, м ║

╠════════╤═══════════╤══════════════╤═════════════╤══════════╣

║ (T) │ (O) │ (B) │ (C) │ (Z) ║

╟────────┼───────────┼──────────────┼─────────────┼──────────╢

║ 11.00 │ 24.1 │ 19.7 │ 95.8 │ 7.96 ║

║ 10.45 │ 24.1 │ 19.7 │ 95.8 │ 7.96 ║

║ 9.90 │ 24.1 │ 19.7 │ 95.8 │ 7.96 ║

║ 9.35 │ 21.8 │ 17.3 │ 85.0 │ 7.80 ║

║ 8.80 │  17.3 │ 12.8 │ 64.8 │ 7.48 ║

║ 8.25 │ 13.2 │ 8.9 │ 47.3 │ 7.15 ║

║ 7.70 │ 9.4 │ 5.7 │ 32.2 │ 6.82 ║

║ 7.15 │ 6.1 │ 3.1 │ 19.7 │ 6.49 ║

║ 6.60 │ 3.3 │ 1.4 │ 10.2 │ 6.15 ║

║ 6.05 │ 1.2 │ .3 │ 3.4 │ 5.82 ║

║ 5.50 │ .0 │ .0 │ .0 │ 5.48 ║

║ 4.95 │ -- │ -- │ -- │ -- ║

║ 4.40 │ -- │ -- │ -- │ -- ║

║ 3.85 │ -- │ -- │ -- │ -- ║

║ 3.30 │ -- │ -- │ -- │ -- ║

║ 2.75 │ -- │ -- │ -- │ -- ║

║ 2.20 │ -- │ -- │ -- │ -- ║

║ 1.65 │ -- │ -- │ -- │ -- ║

║ 1.10 │ -- │ -- │ -- │ -- ║

║ .55 │ -- │ -- │ -- │ -- ║

╚════════╧═══════════╧══════════════╧═════════════╧══════════╝

Для посадки судна по ГВЛ прямо и на ровный киль необходимо рассчитать вес принимаемого балласта P и определить центр его тяжести X_g. Данные величины рассчитываются с использованием кривых теоретического чертежа.

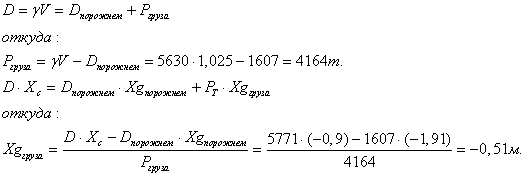
Значения V и X_c снимаем с соответствующих кривых теоретического чертежа на пересечении их с ГВЛ.

Как видим, вычисленные нами расчетные значения отличаются от полученных в программе S1 незначительно. Расхождение составляет 60т. и 0.06м. соответственно.

4.  РАСЧЕТ ПОСАДКИ И ОСТОЙЧИВОСТИ СУДНА

Плавучестью называют способность судна путем вытеснения равного ему по весу и массе количества воды поддерживать вертикальное равновесие в заданном положении относительно поверхности моря.

Мерами плавучести судна являются его объемное водоизмещение V и водоизмещение (масса) судна D = V, где  — плотность забортной воды, т/м³.

На судно, плавающее в положении равновесия на спокойной поверхности воды, действуют силы веса всех его частей и силы гидростатического давления воды на подводную часть его корпуса. Эти силы приводятся к двум равнодействующим: силе веса Р, действующей вертикально вниз, приложенной в центре тяжести судна G и являющейся равнодействующей сил веса всех его частей, и силе плавучести V, действующей вертикально вверх, приложенной в центре величины (центре тяжести подводного объема) судна С и являющейся равнодействующей вертикальных составляющих гидростатических сил давления воды на подводную часть его корпуса. Здесь  — удельный вес забортной воды, кН/м³.

Горизонтальные составляющие гидростатических сил давления воды взаимно уравновешиваются.

Свободно плавающее судно занимает такое положение, при котором его центр величины располагается на одной вертикали с центром тяжести. При этом судно может иметь крен и дифферент.

Величина крена и дифферента характеризует посадку судна.

Остойчивость можно определить как способность судна, отклоненного внешним моментом от положения равновесия, возвращаться в исходное положение равновесия после устранения момента, вызвавшего отклонение.

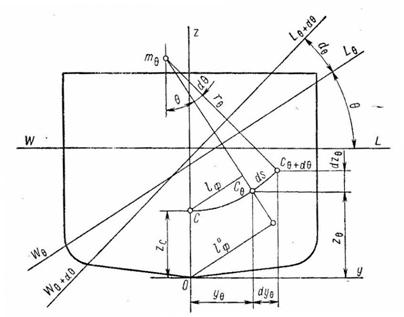
Рис. 4.1 Определение координат центра величины и плеч остойчивости формы

Плечо остойчивости (плечо восстанавливающего момента):

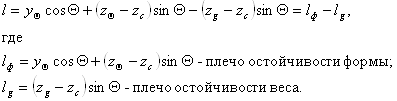
Производная плеча статической остойчивости по углу крена есть возвышение метацентра над центром тяжести корабля или обобщенная метацентрическая высота:

При динамическом воздействии внешних сил в качестве меры остойчивости используется работа восстанавливающего момента Т в процессе наклонения до угла Q:

Рис. 4.2 Пример диаграммы динамической остойчивости

Кривая l_дин(Q) является интегральной кривой по отношению к диаграмме статической остойчивости и называется диаграммой динамической остойчивости.

Здесь и далее, при проведении расчетов полагаем, что данное судно – пассажирское судно неограниченного района плавания. Форма обводов корпуса, коэффициент общей полноты (0,576) и коэффициент полноты ватерлинии корпуса (0,733) характерны именно для пассажирских судов.

В данном разделе приведены результаты расчетов посадки и остойчивости судна.

программа S1 - DERGUNOV.OS5 Таблица 4.1

 ╔════════════════════════════════════════════════════════════════════╗

 ║ Расчет посадки и остойчивости - исходные данные Вариант : 05 ║

 ╟────────────────────────────┬───────────┬─────────┬────────┬────────╢

 ║ название статьи нагрузки │ P,т │ Xg,м │ Yg,м │ Zg,м ║

 ╟────────────────────────────┼───────────┼─────────┼────────┼────────╢

 ║ корпус металлический │ 1607.00 │ -1.91 │ .00 │ 4.87 ║

 ╟────────────────────────────┼───────────┼─────────┼────────┼────────╢

 ║ балласт │ 4224.00 │ -.57 │ .00 │ 6.00 ║

 ╟────────────────────────────┼───────────┼─────────┼────────┼────────╢

 ║ сумма │ 5831.00 │ -.94 │ .00 │ 5.69 ║

 ╚════════════════════════════╧═══════════╧═════════╧════════╧════════╝

Рис. 4.3. Посадка судна в грузу

Рис. 4.4. Наклонения судна в грузу

Таблица 4.2

╔════════════════════════════════════════════════════╗

║ Pасчет посадки и остойчивости ║

║ Результаты - Вариант 05 ║

╟────────────────────────────────────────────────────╢

║ водоизмещение, м**3  5688.76 ║

║ крен, град .00 ║

║ дифферент, град .00 ║

║ осадка носом, м 6.15 ║

║ осадка на миделе, м 6.15 ║

║ осадка кормой, м 6.15 ║

║ нач. попер. метацентр. высота, м .61 ║

╟────────────────────────────────────────────────────╢

║ Pасчет с учетом сопутствующего дифферента ║

╟────────────────────────────────────────────────────╢

║ (O) - угол крена, град ║

║ (Tm) - осадка на ДП, м ║

║ (Yc) - ордината центра величины, м ║

║ (Zc) - аппликата центра величины, м ║

║ (ls) - плечо статической остойчивости, м ║

║ (ld) - плечо динамической остойчивости, м ║

╟───────┬────────┬────────┬────────┬────────┬────────╢

║ (O) │ (Tm) │ (Yc) │ (Zc) │ (ls) │ (ld) ║

╟───────┼────────┼────────┼────────┼────────┼────────╢

║ .00 │ 6.15 │ .00 │ 3.32 │ .00 │ .00 ║

║ 2.50 │ 6.15 │ .13 │ 3.33 │ .03 │ .00 ║

║ 5.00 │ 6.12 │ .27 │ 3.32 │ .06 │ .00 ║

║ 7.50 │ 6.12 │ .40 │ 3.34 │ .09 │ .01 ║

║ 10.00 │ 6.15 │ .53 │ 3.38 │ .13 │ .01 ║

║ 15.00 │ 6.10 │ .81 │ 3.43 │ .20 │ .02 ║

║ 20.00 │ 6.10 │ 1.09 │ 3.53 │ .29 │ .04 ║

║ 25.00 │ 6.07 │ 1.36 │ 3.61 │ .36 │ .07 ║

║ 30.00 │ 6.07 │ 1.61 │ 3.73 │ .41 │ .11 ║

║ 35.00 │ 6.13 │ 1.81 │ 3.86 │ .44 │ .14 ║

║ 40.00 │ 6.23 │ 1.98 │ 4.00 │ .43 │ .18 ║

║ 45.00 │ 6.35 │ 2.12 │ 4.14 │ .41 │ .22 ║

║ 50.00 │ 6.45 │ 2.25 │ 4.25 │ .35 │ .25 ║

║ 55.00 │ 6.60 │ 2.36 │ 4.38 │ .28 │ .28 ║

║ 60.00 │ 6.95 │ 2.41 │ 4.49 │ .17 │ .30 ║

║ 65.00 │ 7.25 │ 2.49 │ 4.59 │ .05 │ .31 ║

║ 70.00 │ 8.00 │ 2.50 │ 4.70 │ -.07 │ .31 ║

║ 75.00 │ 8.75 │ 2.50 │ 4.80 │ -.21 │ .29 ║

║ 80.00 │ 8.75 │ 2.50 │ 4.80 │ -.21 │ .28 ║

╚═══════╧════════╧════════╧════════╧════════╧════════╝

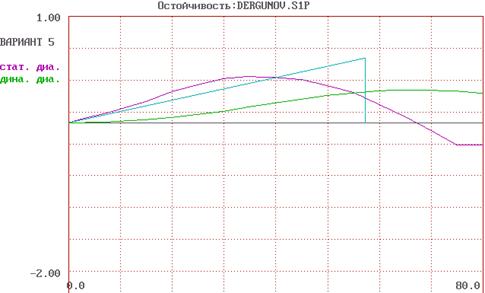
Рис. 4.5. Диаграммы статической и динамической остойчивости