Навигация
Синтеза и анализ комбинационных схем
Содержание
1. Полный дешифратор с прямыми выходами
2. Полный дешифратор с инверсными выходами
3. Неполный дешифратор (дешифратор кода Джонсона)
4. Шифратор (4-канальный приоритетный шифратор прерываний)
5. Мультиплексор. Мультиплексор-демультиплексор
6. Синтез КС на мультиплексорах (арифметический сумматор)
7. Преобразователь кода Грея в двоичный код 8-4-2-1
8. Узел свертки по четности
Список литературы
1. Полный дешифратор с прямыми выходами
Дешифраторами называются КС, входящие в группу преобразователей кодов. Дешифратор (декодер) преобразует входной n-разрядный двоичный код в унитарный (позиционный) код. В унитарном коде только на одной позиции разряд принимает активное значение: на одной позиции 1, на остальных – 0 (в дешифраторах с прямыми выходами) или на одной позиции 0, на остальных – 1 (в дешифраторах с инверсными выходами).
В зависимости от количества выходов k (количества разрядов в выходном позиционном коде) дешифраторы могут быть полными, неполными или селекторами. Полный дешифратор имеет n входов и k = 2nвыходов, неполный – n входов и k < 2nвыходов, селектор – n входов и 1выход.
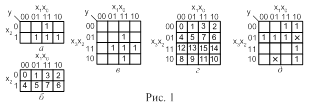
На рис. 10,а приведена таблица истинности для полного дешифратора 3×8 (3 входа, 8 выходов) с прямыми выходами, на рис.10,б – его условное графическое обозначение в соответствии с ЕСКД, на рис. 10,в – результаты его синтеза на ЛЭ основного базиса.
Из таблицы истинности следует, что дешифратор реализует систему выходных логических функций y0 ,...,y7 от входных переменных x2, x1, x0. Каждая функция содержит только одно единичное значение, поэтому ее представление в СДНФ имеет вид yi = mi. Все реализуемые дешифратором выходные функции приведены на рис. 10,в.
Из сказанного следует, что полный дешифратор на своих выходах реализует полный набор (2n) минтермов. Поэтому дешифратор может быть применен для реализации произвольных ПФ (систем произвольных ПФ). Для этого ПФ представляются в СДНФ через дизъюнкцию соответствующих минтермов.
2. Полный дешифратор с инверсными выходами
На рис.11,а приведена таблица истинности для полного дешифратора 3×8 с инверсными выходами, на рис.11,б его условное графическое обозначение и реализуемые выходные функции. Такой дешифратор реализует на своих выходах полный набор макстермов Mi, так как все его выходные функции содержат только одно нулевое значение. Дешифратор с инверсными выходами также можно применять для реализации произвольных ПФ, представленных в СКНФ через конъюнкцию макстермов.
Сигнал E для дешифраторов является сигналом разрешения его работы (E=1), если E = 0 – не формируется ни один минтерм (рис.10,б), ни один макстерм (рис.11,б).
3. Неполный дешифратор (дешифратор кода Джонсона)
Приведенные примеры полных дешифраторов показывают, что при получении схем не выполнялась минимизация выходных функций, так как отсутствуют соседние минтермы или макстермы.
Неполный дешифратор формирует неполный набор минтермов (макстермов) – N из возможных 2n для полного дешифратора (N < 2n). Следовательно, в составе наборов входных переменных нет кодовых комбинаций, соответствующих отсутствующим минтермам (макстермам). Отсутствующие кодовые комбинации являются факультативными, что является основанием для минимизации функций выходов дешифратора и может уменьшить сложность схемы неполного дешифратора. В таком случае неполный дешифратор является специализированным преобразователем кода, который для заданных входных кодовых комбинаций формирует соответствующие контермы (дизтермы).
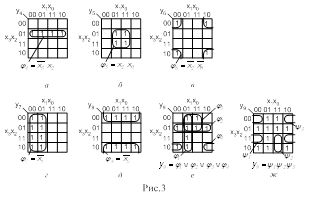
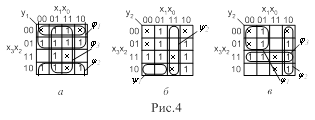
На рис.12 приведен пример синтеза неполного дешифратора для декодирования кода Джонсона. Код Джонсона - специальный цифровой код заданной разрядности n, в котором кодовые комбинации формируются путем “вытеснения” единиц нулями, затем – наоборот (см. пример на рис.12,а для n = 3). Количество комбинаций кода Джонсона N = 2n.
Таблица истинности для рассматриваемого примера (рис.12,а) имеет всего 6 строк, отсутствуют наборы с номерами 2 и 5, которые являются факультативными, и которым в картах Карно для выходных функций дешифратора (рис.12,б) соответствуют клетки, обозначенные знаком ×.
Минимизация по картам Карно выходных функций дешифратора с включением в подкубы факультативных клеток приводит к получению для всех функций контермов второго ранга (вместо минтермов третьего ранга для полного дешифратора). Специализированный дешифратор для декодирования кода Джонсона (рис.12,в) требует меньших аппаратных затрат по сравнению с полным дешифратором 3×23, который тоже можно для этого использовать, задействовав нужные выходы.
4. Шифратор (4-канальный приоритетный шифратор прерываний)
Шифраторами называются КС, входящие в группу преобразователей кодов. Шифратор решает задачу, обратную задаче дешифратора. Шифратор (кодер) преобразует входной унитарный (позиционный) код в выходной двоичный код.
При проектировании микропроцессорных устройств часто возникает ситуация, когда несколько периферийных устройств (ПУ) одновременно хотят связаться с микропроцессором (МП) для того, чтобы выполнить определенные совместные действия (подпрограмму, запрашиваемую ПУ). В этом случае говорят, что ПУ вырабатывает сигнал прерывания с целью прервать текущую работу МП и перейти на подпрограмму обслуживания этого ПУ.
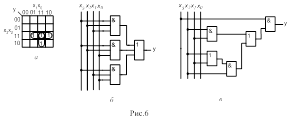
Логической задачей обработки всех запросов прерываний для КС, представленной на рис 13,а, является выработка для МП сигнала INT, если есть хотя бы один запрос I0, I1, I2, I3 на прерывание от ПУ и получение кода ПУ, сделавшего запрос (адресного кода A1A0) , по которому МП находит требуемую подпрограмму. При наложении запросов (при совпадении по времени) КС формирует адрес ПУ, имеющего высший приоритет. КС, решающая такую задачу, называется приоритетным шифратором.
Таблица истинности рис.13,б отображает логику работы приоритетного шифратора. Наивысший приоритет имеет запрос I0, низший - I3. Символ ![]() показывает, что запрос низкого приоритета игнорируется при совпадении с запросом более высокого приоритета.
показывает, что запрос низкого приоритета игнорируется при совпадении с запросом более высокого приоритета.
Результаты минимизации логических функций INT,A1,A0 и КС для их реализации на ЛЭ основного базиса приведены на рис. 13,в,г.
Похожие работы
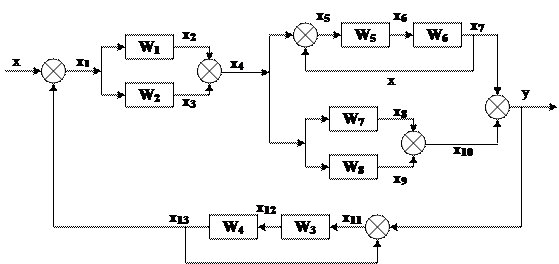
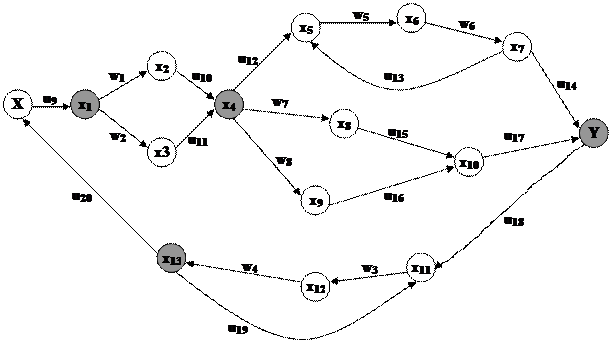
... D=1- W3W4(W1W5W6+ W7+ W1W8+ W2W6 W7+ W2W7+2W2W8+ 1)+ W5W6(W3W4(W7+ W1W5W6+ W2W7+ W2W8+1)-1) Для x1 Для x4 Для y Для х13 Задание 2. Синтез комбинационных схем. 2.1 Определение поставленной задачи Устройство, работа которого может быть представлена на языке алгебры высказываний, принято называть логическим. Пусть такое устройство имеет n ...
... порядка рис.7,б, которая хуже схемы рис.7,а по характеристикам быстродействия и сложности. Ухудшение характеристик оправдывается только возможностью реализации схемы на заданных стандартных элементах. 8. Комбинационные схемы Логическая схема (рис.8) с n входами и k выходами реализует систему переключательных функций y0 ...yk-1. Каждая функция yi(x0 ...xk-1) однозначно соответствует ...
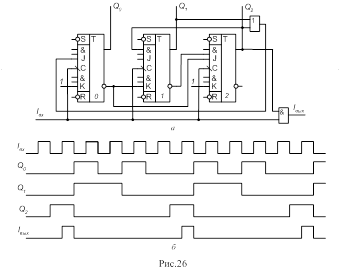
... формировать счетчик, называют модулем счета М (коэффициентом счета). После поступления на счетчик М входных сигналов начинается новый цикл, повторяющий предыдущий. Примером счетчика может быть последовательностное устройство рис.3,а, в котором для каждого из пяти импульсов на входе Iвх формируется трехразрядный код на выходах . Работа счетчика описывается графом рис.1,б или таблицей состояний на ...
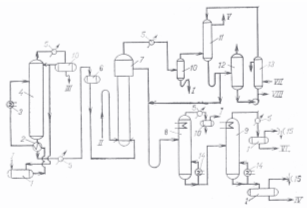
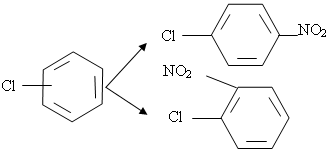
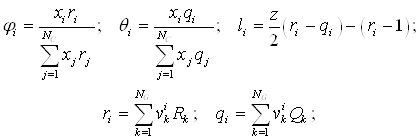
... 8,6961 6,6957 9,9694 - Энергозатраты по схемам ГДЖ/ч 10,0379 15,3918 9,9624 7. Выводы В результате проделанной работы решена задача разделения промышленной смеси продуктов синтеза хлорбензола. В качестве модели наиболее адекватно описывающей парожидкостное равновесие смеси была выбрана модель UNIFAC. Были синтезированы две схемы, состоящие из двух простых двухсекционных колонн ...
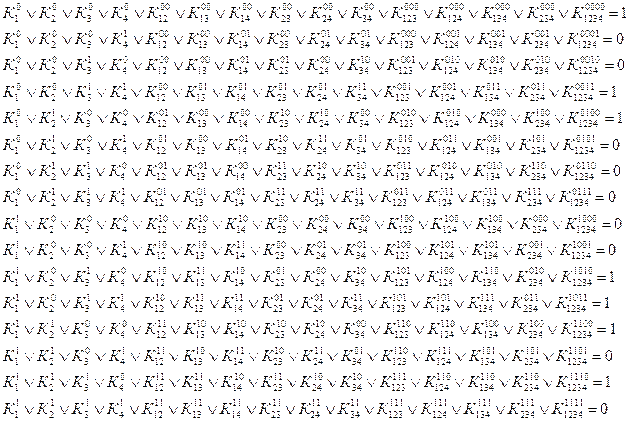
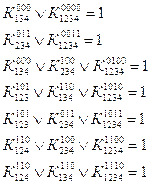
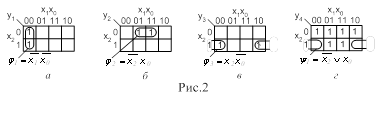
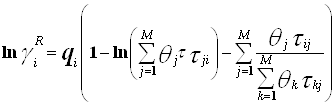
0 комментариев