Навигация
Содержание
1. Основные аксиомы, теоремы и тождества алгебры логики
2. Переключательные функции
3. Не полностью определенные переключательные функции
4. Построение комбинационной логической схемы по заданной переключательной функции
5. Минимизация переключательных функций с помощью карт Карно
6. Нормальные формы логических уравнений. Преобразование логических уравнений к заданному базису
7. Скобочные формы логических уравнений
8. Комбинационные схемы
Список литературы
1. Основные аксиомы, теоремы и тождества алгебры логики
Методы синтеза и анализа всех классов цифровых схем построены на базе алгебры логики, которая является основным математическим аппаратом описания и преобразования структуры цифровых схем [1].
В алгебре логики рассматриваются переменные, которые могут принимать только два значения: 0 и 1 (например, 0 – событие не происходит, 1 – происходит; 0 – ложное высказывание, 1 – истинное; 0 – низкий уровень напряжения, 1 – высокий; 0 – разомкнутый контакт, 1 - замкнутый). Значения переменных не отображают каких-либо количественных значений, а имеют лишь символическое значение.
Основные соотношения алгебры логики приведены в табл. 1. В справедливости приведенных соотношений можно убедиться, используя метод перебора. При преобразовании логических выражений, как и в обычной алгебре, должен соблюдаться порядок выполнения операций (порядок старшинства операций) – сначала отрицание, затем конъюнкция и потом дизъюнкция. Приведенный порядок выполнения операций можно изменить и задать его с помощью скобок. В тождествах (9.1) – (12.2) правая часть проще левой, поэтому их можно использовать для упрощения сложных логических выражений.
Все тождества записаны парами на основании того, что по принципу двойственности из одного тождества пары можно получить другое взаимной заменой операций дизъюнкции и конъюнкции, а также значений 0 и 1. Тождества (4.1) и (4.2) самодвойственны, так как они не изменяются по принципу двойственности.
Большую роль в теории переключательных функций играет операция сумма по модулю два (исключающее ИЛИ, логическая неравнозначность), которая обозначается символом ![]() и определяется соотношением
и определяется соотношением
![]()
Операция сумма по модулю два коммутативна, ассоциативна и дистрибутивна относительно операции конъюнкции.
2. Переключательные функции
Любое логическое выражение, составленное из n переменных с помощью конечного числа операций алгебры логики, можно рассматривать как некоторую функцию n переменных. Двоичная функция может принимать только два значения: 0 и 1 – в зависимости от значений переменных. Такие функции являются удобным инструментом для описания, анализа и синтеза переключательных схем (бесконтактных и контактных), поэтому они называются переключательными функциями (ПФ).
Для ПФ n переменных x0,…,xn-1 будем использовать обозначение y (x0,…,xn-1). Совокупность значений переменных, в которой каждая переменная может принимать значения 0 или 1, называется набором. Любая функция n переменных может быть определена на 2n наборах. Это следует из того, что каждому набору соответствует n-разрядное двоичное число, а количество различных двоичных чисел при n разрядах равно 2n.
Существуют несколько способов задания ПФ.
1. Табличный, когда функция задается в виде таблицы истинности (соответствия). Таблица истинности содержит 2n строк ( по числу наборов), n столбцов значений аргументов и один столбец значений функции. В таблице каждому набору аргументов соответствует значение функции.
Таблица истинности ПФ, значения которой соответствуют значениям, принимаемым большинством переменных в наборе (функция голосования), определяет ПФ мажоритарного элемента “два из трех” (переноса двоичного разряда.
2. Координатный способ, когда функция задается в виде координатной карты состояний, например в виде карты Карно. Карта содержит 2n клеток по числу наборов значений переменных. Каждая клетка задается координатами строки и столбца, соответствующими определенному набору. Все аргументы разбиваются на две группы так, что одна группа определяет координаты строки, а другая – столбца. Порядок записи значений переменных в каждой группе задается записью переменных в соответствующем порядке над столбцами и около строк. Кодовые комбинации, задающие координаты двух соседних столбцов (строк), соответствуют двум соседним кодовым комбинациям циклического кода Грея .Соседние комбинации такого кода отличаются значениями только одной переменной. Значение функции на данном наборе проставляется внутри клетки (клетки, соответствующие нулевым значениям ПФ, часто в целях наглядности оставляют пустыми).

На рис. 1,а приведена карта Карно для ПФ мажоритарного элемента “два из трех”, заданной таблицей истинности 2, на рис.1,в – для ПФ компаратора. На рис.1,б,г в клетках проставлены их номера, соответствующие номерам наборов.
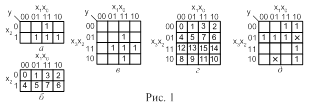
Карты Карно являются важным средством проектирования логических схем. Особенность карт в том, что любые две соседние клетки отличаются значением какой-либо одной и только одной переменной. Эта особенность характеризует также клетки первой и последней строк, первого и последнего столбцов, поэтому такие клетки тоже можно считать соседними. Указанная особенность соседних клеток позволяет легко осуществлять упрощение ПФ посредством использования тождества склеивания.
3. Числовой способ, когда ПФ задается в виде десятичных номеров тех наборов переменных, на которых функция принимает значение 1. При этом следует учитывать, что i-я двоичная переменная имеет “вес” 2i. Например, приписывая переменным x2,x1,x0 соответственно “веса” 22,21,20, в числовом виде ПФ рис.1,а будет задана как y( x2,x1,x0 ) = ![]() ( 3, 5, 6, 7 ).
( 3, 5, 6, 7 ).
Можно использовать для задания функции десятичные номера наборов, на которых функция принимает значение 0. Та же ПФ (рис.1,а) в таком случае будет задана как y( x2,x1,x0 ) = ![]() ( 0, 1, 2, 4 ).
( 0, 1, 2, 4 ).
4. Аналитический способ, когда ПФ задается в виде алгебраического выражения (структурной формулы), получаемого путем применения логических операций к аргументам ПФ. Следует учитывать, что одну и ту же ПФ можно задать в виде разных структурных формул, которые отличаются друг от друга выбором используемых логических операций и своей сложностью.
При использовании всех n аргументов для записи алгебраического выражения существует две формы структурных формул.
Совершенная дизъюнктивная нормальная форма (СДНФ) представляет собой дизъюнкцию минтермов.
Минтерм (минимальный терм, конституента единицы) есть логическое произведение всех переменных ПФ для наборов, на которых ПФ принимает значение 1.Если в наборе переменная равна 1, то в минтерм эта переменная входит без инверсии, если равна 0 - то с инверсией. Например, если на наборе x2 = 0, x1 = 1, x0 =1 ПФ принимает значение 1, то соответствующий минтерм m3 для третьего набора будет иметь вид m3 =![]() x1 x0 .
x1 x0 .
Пример: СДНФ для ПФ мажоритарного элемента (рис.1,а)
y= m3![]() m5
m5![]() m6
m6![]() m7
m7![]() (1)
(1)
Совершенная конъюнктивная нормальная форма (СКНФ) представляет собой конъюнкцию макстермов.
Макстерм (максимальный терм, конституента нуля) есть логическая сумма всех переменных ПФ для наборов, на которых ПФ принимает значение 0. Если в наборе переменная равна 1, то в макстерм эта переменная входит с инверсией, если равна 0 - то без инверсии. Например, если на наборе x2 = 0, x1 = 0, x0 =1 ПФ принимает значение 0, то соответствующий макстерм M1 для первого набора будет иметь вид ![]() .
.
Пример: СКНФ для ПФ мажоритарного элемента (рис.1,а)
y =M0M1M2M4 =(![]() )(
)(![]() )(
)(![]() )(
)(![]() ).(2)
).(2)
Минтермы (макстермы) называются соседними, если они отличаются формой представления только одной переменной (без инверсии, с инверсией). В примере (1) минтерм m7 является соседним по отношению ко всем остальным (m3, m5, m6). В примере (2) макстерм М0 является соседним по отношению ко всем остальным (М1,М2,М4).Признак соседства минтермов (макстермов) используется при применении закона склеивания (при минимизации ПФ с применением карт Карно).
Определение “совершенная форма” означает, что все минтермы или макстермы имеют одинаковую размерность (ранг), равную числу переменных n, от которых зависит ПФ.
Определение “нормальная форма” означает, что порядок логического уравнения не более двух. Порядок логического уравнения – количество последовательно выполняемых базовых операций алгебры логики при вычислении значения функции (операция инверсии в расчет не принимается). При реализации логических схем порядок ПФ определяет число каскадов логического преобразования входных переменных, необходимых для получения функции.
Можно привести и более простые алгебраические выражения для ПФ мажоритарного элемента (рис.1,а):
![]() (3)
(3)
y = (![]() )(
)(![]() )(
)(![]() )(4)
)(4)
Способ их получения рассмотрен ниже.
Похожие работы
... базис применением теорем де Моргана в любой последовательности. Последнее справедливо, в силу того, что применение теорем де Моргана не изменяет числа букв в выражении. 3.Проектирование комбинационных схем с учетом коэффициентов объединения по входу и выходу Допустимая величина коэффициента объединения по входу (І) в реальных условиях проектирования КС оказывает существенное влияние на ...
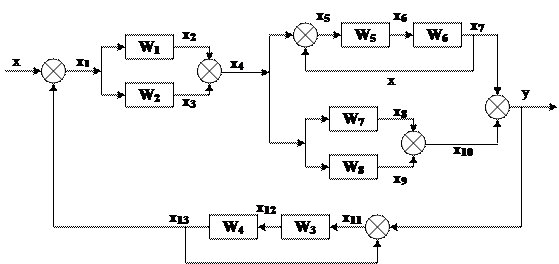
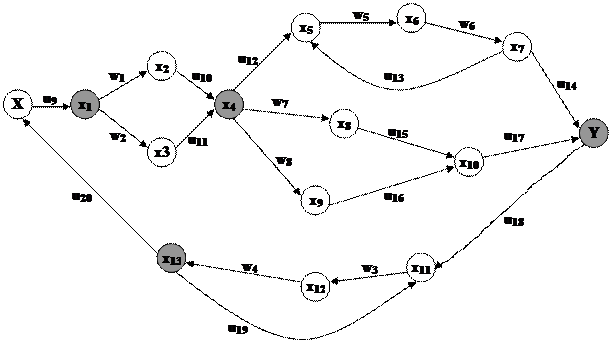
... D=1- W3W4(W1W5W6+ W7+ W1W8+ W2W6 W7+ W2W7+2W2W8+ 1)+ W5W6(W3W4(W7+ W1W5W6+ W2W7+ W2W8+1)-1) Для x1 Для x4 Для y Для х13 Задание 2. Синтез комбинационных схем. 2.1 Определение поставленной задачи Устройство, работа которого может быть представлена на языке алгебры высказываний, принято называть логическим. Пусть такое устройство имеет n ...
... 1 1 0 1 0 0 14 1 1 1 0 0 0 15 1 1 1 1 0 1 Для выполнения синтеза логической схемы необходимо произвести следующие действия: 1.по таблице истинности составить логические уравнения для каждого выхода в виде СДНФ и СКНФ; 2.для получения наиболее простой логической схемы выполнить минимизацию функций, записанных в СДНФ и СКНФ, используя метод непосредственных преобразований; 3. ...
... чертеж или схема выполняются в САПР AutoCAD, поэтому наиболее часто используемой вспомогательной программой является конвертор из формата P-CAD в AutoCAD. 1. Основы математического аппарата анализа и синтеза комбинационных логических устройств Все устройства, оперирующие с двоичной информацией, подразделяются на два класса: - комбинационные (дискретные автоматы без памяти). - ...



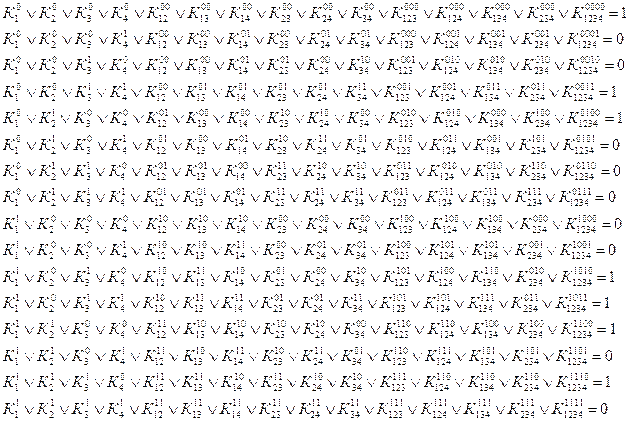
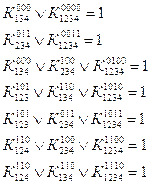
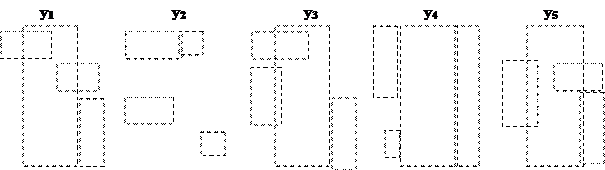


0 комментариев