Навигация
Мультиплексор. Мультиплексор-демультиплексор
5. Мультиплексор. Мультиплексор-демультиплексор
Мультиплексорами называются КС, входящие в группу коммутационных узлов, работающие как переключатели цифровых сигналов. Логику работы мультиплексора раскрывает 4-канальная (4-входовая) механическая модель коммутатора (рис.14,а). Подвижный контакт коммутатора К устанавливается в позицию, задаваемую двухразрядным адресным кодом А1, А0, и соединяет соответствующий неподвижный контакт с выходом y .
При этом на выход поступает выбранный с помощью адресного кода цифровой сигнал Di.
Условное графическое обозначение 4-канального мультиплексора (MUX) приведено на рис.14,б, а на рис.14,в – обобщенная таблица истин- ности, отображающая логику его работы. Структурная формула (рис.14,в) для логической функции выхода мультиплексора y получена из таблицы истинности в СДНФ и представлена затем через минтермы, реализуемые дешифратором 2×22. Структурная схема 4-канального дешифратора, составленная на основе дешифратора, показана на рис.14,г.
Демультиплексор (рис.15) выполняет операцию, обратную операции мультиплексора (рис.14,а), коммутирует сигнал D на один из 2n выходов, где n – разрядность адресного кода выхода yi.
В качестве демультиплексора можно использовать полный дешифратор с входом разрешения E (рис.10,б,в). Если подать коммутируемый сигнал D на вход разрешения E (E = D), то на адресуемом выходе дешифратора будет сигнал, эквивалентный сигналу D.
Демультиплексор можно также реализовать на основе использования интегральных схем (рис. 14,д), называемых мультиплексоры-демультиплексоры. В структуру такой схемы входят дешифратор и аналоговые ключи (АК). Аналоговые ключи выполняются по КМОП-технологии и позволяют создавать схемы с двунаправленной передачей сигналов как в аналоговой, так и в цифровой форме. Ключ управляется цифровым сигналом zi, переводящим его в замкнутое состояние (zi = 1 - сопротивление ключа мало), или разомкнутое (zi= 0 - сопротивление ключа велико). Для аналоговых ключей входы и выходы неразличимы, поэтому любой вход xi может служить выходом, а любой выход yi- входом.
Мультиплексор-демультиплексор (рис. 14,д) выполняет функцию демультиплексора, если соединить все входы x = x0 =x1 = x2 =x3 и на объединенный вход x подать сигнал D, тогда выходами являются линии y0, y1, y2, y3 . Для получения мультиплексора соединяются все выходы, и объединенный выход y = y0 = y1 = y2 = y3 является выходом мультиплексора.
6. Синтез КС на мультиплексорах (арифметический сумматор)
Логическая функция, реализуемая мультиплексором (рис.14,в) с n адресными входами, по структуре полностью совпадает с СДНФ для функций n переменных (1). Из этого следует, что любую ПФ n переменных можно реализовать тривиальным прямым способом, подав переменные на адресные входы, а на входы Di - константы 0 или 1.
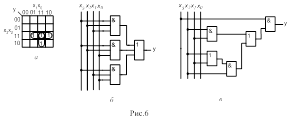
Более эффективен (по критерию затрат аппаратных средств) способ реализации ПФ на основе мультиплексора, когда на информационные входы Di подаются не только константы 0 и 1, но и переменные и некоторые функции от переменных, выполняемые простыми ЛЭ (рис.16). В этом случае 4-канальный мультиплексор, имеющий два адресных входа, можно использовать для реализации функции трех переменных y( x2,x1,x0 ).
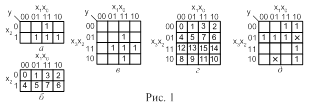
В качестве примера рассмотрим синтез логической схемы одноразрядного арифметического полного сумматора на основе 4-канальных мультиплексоров. Таблица истинности сумматора приведена на рис.17,а. В таблице: ai и bi – суммируемые разряды, pi-1 - перенос из (i-1)-го разряда; si - значение суммы; pi – перенос из i-го в (i+1)-й разряд.
В СДНФ логическая функция переноса piимеет вид:
![]() . (12)
. (12)
Примем в качестве адресных переменных A1, A0 соответственно переменные ![]() и перепишем уравнение (12) в виде, соответствующем логическому уравнению 4-канального мультиплексора (рис.14,в)
и перепишем уравнение (12) в виде, соответствующем логическому уравнению 4-канального мультиплексора (рис.14,в)
![]() . (13)
. (13)
Из сопоставления уравнения (13) и уравнения 4-канального мультиплексора (рис.14,в) следует: D0 = 0, D1 = pi-1, D2 = pi-1, D3 = (![]() ) = 1.
) = 1.
Проще и нагляднее получаются функции входов мультиплексора при использовании карт Карно. При сделанном выборе адресных переменных каждому из четырех информационных входов мультиплексора соответствует одна из четырех зон карты Карно, показанных на рис.17,б. Каждую из этих зон можно рассматривать как двухклеточную карту Карно, которая задает логическую зависимость сигнала входа Di мультиплексора от переменной pi-1, не используемой в качестве адресной переменной. Для выявления этой логической связи необходимо сопоставить значения, принимаемые переменной pi-1, и значения функции (piили si), записанные в клетках карты. Эти значения либо равны, либо находятся в инверсной связи, либо значение функции не зависит от переменной pi-1 (равно 0 или 1).
Полученные по картам значения функций входов мультиплексоров приведены на рис.17,в,г, а на рис.17,д – соответствующая им структурная схема арифметического сумматора, выполненная на двух мультиплексорах с общими адресными входами. На рис.17,е – условное графическое обозначение одноразрядного арифметического полного сумматора. Многоразрядные арифметические сумматоры (рис.17,ж – арифметический сумматор двух четырехразрядных двоичных чисел) строятся на основе одноразрядных арифметических сумматоров (рис.17,е), на рис.17,з – условное графическое обозначение такого сумматора.
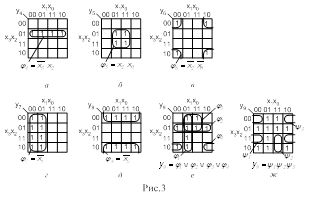
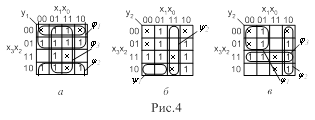
Для функций трех переменных y( x2,x1,x0 ) возможны три варианта выбора адресных переменных А1,А0 (рис.18,а). Каждому варианту соответствует свой способ разделения карты Карно на четыре зоны, определяющие логические функции информационных входов Dj .
На рис.18,б приведены все возможные варианты выбора адресных переменных и разделения карт Карно на зоны, если 4-канальный мультиплексор используется для реализации функции y( x3,x2,x1,x0 ) четырех переменных.
Выбор адресных переменных должен быть оптимальным, так как сложность функций на информационных входах Dj, а значит и КС в целом, в общем случае зависит от сделанного выбора. Критерием оптимальности выбора адресных переменных может служить количество функций, равных 0 и 1, а также сложность функций, не равных 0 и 1. В качестве адресных сигналов следует использовать те переменные, которые входят в МДНФ наибольшее число раз. В этом случае наибольшую логическую нагрузку будет нести внутренний дешифратор мультиплексора. Такой подход к выбору адресных сигналов позволяет исключить полный перебор всех вариантов.
Похожие работы
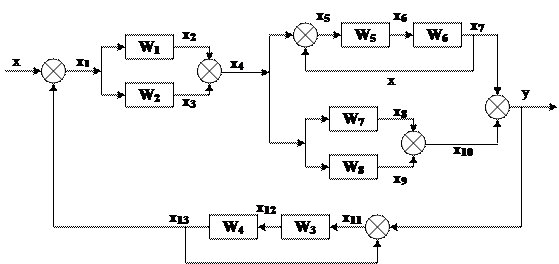
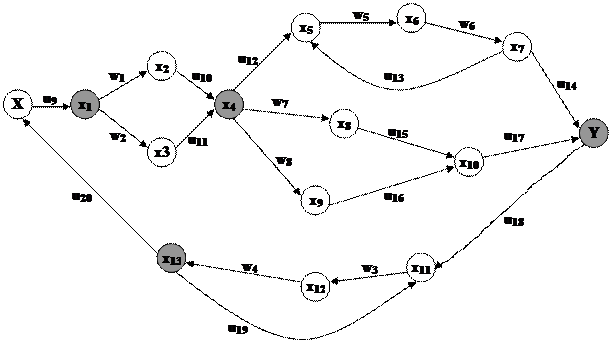
... D=1- W3W4(W1W5W6+ W7+ W1W8+ W2W6 W7+ W2W7+2W2W8+ 1)+ W5W6(W3W4(W7+ W1W5W6+ W2W7+ W2W8+1)-1) Для x1 Для x4 Для y Для х13 Задание 2. Синтез комбинационных схем. 2.1 Определение поставленной задачи Устройство, работа которого может быть представлена на языке алгебры высказываний, принято называть логическим. Пусть такое устройство имеет n ...
... порядка рис.7,б, которая хуже схемы рис.7,а по характеристикам быстродействия и сложности. Ухудшение характеристик оправдывается только возможностью реализации схемы на заданных стандартных элементах. 8. Комбинационные схемы Логическая схема (рис.8) с n входами и k выходами реализует систему переключательных функций y0 ...yk-1. Каждая функция yi(x0 ...xk-1) однозначно соответствует ...
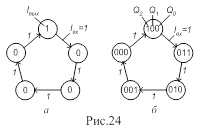
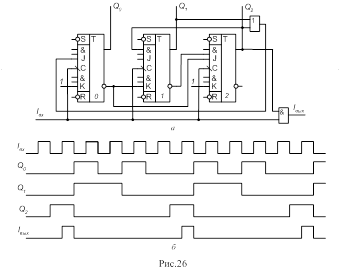
... формировать счетчик, называют модулем счета М (коэффициентом счета). После поступления на счетчик М входных сигналов начинается новый цикл, повторяющий предыдущий. Примером счетчика может быть последовательностное устройство рис.3,а, в котором для каждого из пяти импульсов на входе Iвх формируется трехразрядный код на выходах . Работа счетчика описывается графом рис.1,б или таблицей состояний на ...
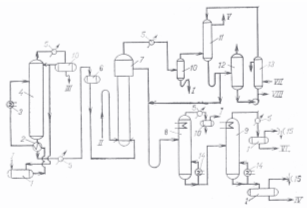
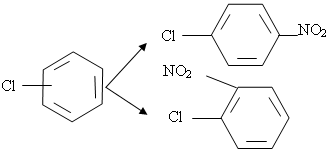
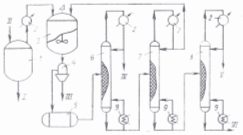
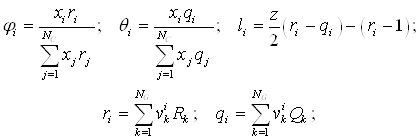
... 8,6961 6,6957 9,9694 - Энергозатраты по схемам ГДЖ/ч 10,0379 15,3918 9,9624 7. Выводы В результате проделанной работы решена задача разделения промышленной смеси продуктов синтеза хлорбензола. В качестве модели наиболее адекватно описывающей парожидкостное равновесие смеси была выбрана модель UNIFAC. Были синтезированы две схемы, состоящие из двух простых двухсекционных колонн ...
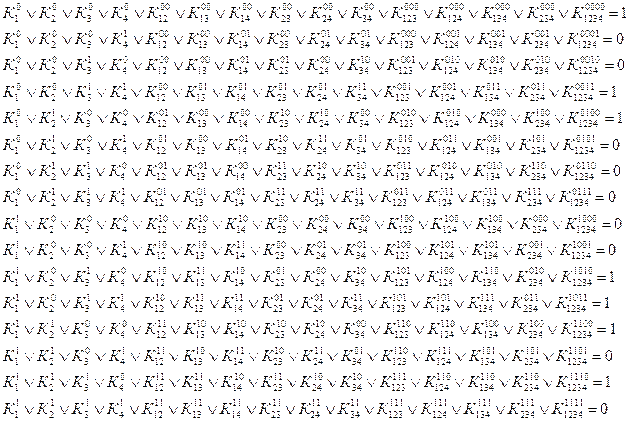
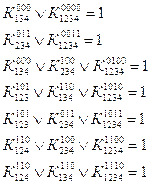
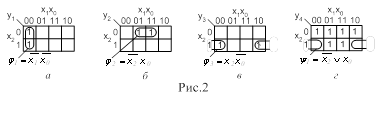
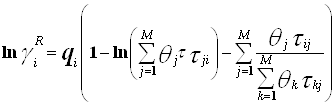
0 комментариев