Навигация
Примеры решения типовых задач
3. Примеры решения типовых задач
Пример 1
Аэростат массой m![]() 250 кг начал опускаться с ускорением
250 кг начал опускаться с ускорением ![]()
![]() 0,2м/с2. Определить массу балласта, который следует сбросить, чтобы аэростат получил такое же ускорение, но направленное вверх. Ускорение свободного падения
0,2м/с2. Определить массу балласта, который следует сбросить, чтобы аэростат получил такое же ускорение, но направленное вверх. Ускорение свободного падения ![]()
![]() 9,8 м/с2. Сопротивлением воздуха пренебречь.
9,8 м/с2. Сопротивлением воздуха пренебречь.
Дано:
![]()
![]() 250 кг;
250 кг;
![]()
![]() 0,2м/с2;
0,2м/с2;
![]()
![]() 9,8 м/с2.
9,8 м/с2.
_______________
![]() m
m ![]() ?
?
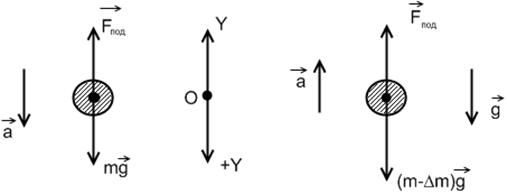
Рис. 2.1.
Решение: Так как аэростат опускается с ускорением ![]() , меньшим ускорения свободного падения
, меньшим ускорения свободного падения ![]() , и по условию задачи сопротивление воздуха отсутствует, то это означает, что на него кроме силы тяжести
, и по условию задачи сопротивление воздуха отсутствует, то это означает, что на него кроме силы тяжести ![]() действует подъемная сила
действует подъемная сила ![]() , направленная вертикально вверх.
, направленная вертикально вверх.
Действующие на аэростат силы направлены вертикально, следовательно, уравнение движения
![]() (1)
(1)
достаточно спроецировать только на одну ось системы координат ![]() OY:
OY:
![]() . (2)
. (2)
Откуда подъемная сила ![]() . (3)
. (3)
Если сбросить балласт массой ![]() , то уравнение движения можно записать в виде
, то уравнение движения можно записать в виде
![]() , (4)
, (4)
или с учетом полученного выражения для подъемной силы ![]() (3)
(3)
![]() (5)
(5)
Следовательно, масса сброшенного балласта равна
![]() 10 кг.
10 кг.
Пример 2
Автомобиль, трогаясь с места, за время ![]()
![]() 5с равноускоренно набирает скорость
5с равноускоренно набирает скорость ![]()
![]() 72 км/ч.
72 км/ч.
Найти минимально возможный коэффициент трения между колесами автомобиля и дорогой при таком движении.
Какой наименьший тормозной путь автомобиля, набравшего эту скорость?
Дано:
![]()
![]() 5с;
5с;
![]()
![]() 72 км/ч
72 км/ч![]() 20 м/с;
20 м/с;
![]()
![]() 9,8 м/с2.
9,8 м/с2.
_________________
![]() ?
? ![]()
![]() ?
?
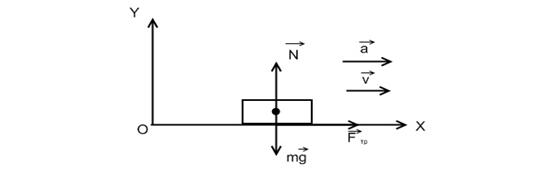
Рис. 2.2
Решение: При движении автомобиля, как при разгоне, так и при торможении, на него действуют три силы: сила тяжести ![]()
![]() , сила нормальной реакции со стороны дороги
, сила нормальной реакции со стороны дороги ![]() и сила трения
и сила трения ![]()
а) При ускоренном движении автомобиля сила трения препятствует проскальзыванию ведущих колес по поверхности дороги, поэтому, она направлена в сторону движения и является силой трения покоя. Именно сила трения покоя ![]() в данном случае будет являться движущей силой. Исходя из выбранной системы координат XOY, уравнение движения имеет вид
в данном случае будет являться движущей силой. Исходя из выбранной системы координат XOY, уравнение движения имеет вид
![]() (1)
(1)
В проекциях на оси системы координат:
ОХ: ![]() , (2)
, (2)
ОY: ![]() . (3)
. (3)
Выразив силу трения через силу реакции ![]() и коэффициент трения
и коэффициент трения ![]() между колесами и дорогой
между колесами и дорогой
![]() , (4)
, (4)
из уравнения движения определим ускорение автомобиля:
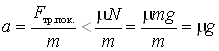 . (5)
. (5)
С другой стороны, так как по условию задачи автомобиль двигаясь равноускоренно за время ![]() приобрел скорость
приобрел скорость ![]() , то его ускорение равно
, то его ускорение равно ![]() . (6)
. (6)
Из выражений (5) и (6) имеем ![]() 0,41. Следовательно,
0,41. Следовательно,
![]() 0,41. (7)
0,41. (7)
б) При торможении сила трения направлена в сторону, противоположную движению и является силой трения скольжения. Уравнение движения автомобиля в этом случае в проекциях на оси координат
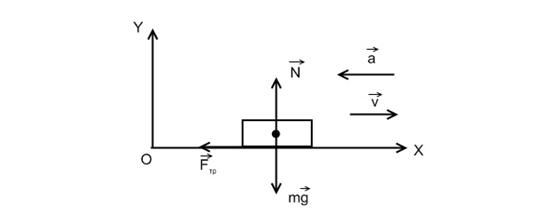
Рис. 2.3.
ОХ: ![]() , (8)
, (8)
ОY: ![]() . (9)
. (9)
Учитывая, что ![]() , ускорение автомобиля при торможении
, ускорение автомобиля при торможении
![]() . (10)
. (10)
Путь, пройденный автомобилем, движущимся равнозамедленно с начальной скоростью ![]() равен
равен
![]() (11)
(11)
Время движения до остановки ![]() можно определить из условия, что конечная скорость автомобиля
можно определить из условия, что конечная скорость автомобиля
![]() следовательно,
следовательно, ![]() (12)
(12)
Тогда ![]() (13)
(13)
Учитывая выражения для коэффициента трения (7), получаем
![]() 50 м.
50 м.
Пример 3
На гладкой наклонной плоскости с углом при основании ![]() лежит доска массой М, а на доске – брусок массой m. На доску действует сила, направленная вверх по склону. При какой величине этой силы, груз начнёт соскальзывать? Коэффициент трения между доской и бруском
лежит доска массой М, а на доске – брусок массой m. На доску действует сила, направленная вверх по склону. При какой величине этой силы, груз начнёт соскальзывать? Коэффициент трения между доской и бруском ![]() . Ускорение свободного падения
. Ускорение свободного падения ![]() .
.
Дано:
![]() ;
;
М;
m;
![]() ;
;
![]() .
.
___________
F ![]() ?
?
Решение: Силы, действующие на каждое из тел, в инерциальной системе отсчета XOY указаны на Рис.2.4.
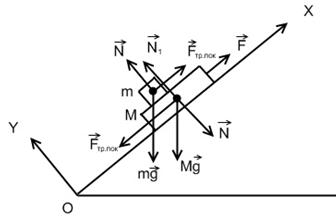
Рис. 2.4
На брусок действует сила тяжести ![]() , сила трения
, сила трения ![]() , сила
, сила ![]() и сила реакции
и сила реакции ![]() ; на доску действует сила тяжести
; на доску действует сила тяжести ![]() , сила реакции
, сила реакции ![]() , сила трения
, сила трения ![]() и вес бруска равный по величине
и вес бруска равный по величине ![]() . Учтём, что
. Учтём, что
![]() . (1)
. (1)
Запишем второй закон Ньютона в проекциях на оси выбранной системы координат при условии, что брусок по доске не скользит:
![]() (2)
(2)
![]() (3)
(3)
![]() . (4)
. (4)
Решая систему уравнений (2) и (3), получим ![]() .
.
Используем условие (1): ![]() .
.
Следовательно, при ![]() брусок будет соскальзывать с доски.
брусок будет соскальзывать с доски.
Пример 4
На наклонной плоскости с углом при основании ![]() неподвижно лежит кубик. Коэффициент трения между клином и кубиком равен
неподвижно лежит кубик. Коэффициент трения между клином и кубиком равен ![]() . Наклонная плоскость движется с ускорением
. Наклонная плоскость движется с ускорением ![]() в направлении, показанном на рис. 2.5. При каком минимальном значении этого ускорения кубик начнет соскальзывать?
в направлении, показанном на рис. 2.5. При каком минимальном значении этого ускорения кубик начнет соскальзывать?
Дано:
![]() ;
;
![]() ;
;
![]() .
.
________
![]() ?
?
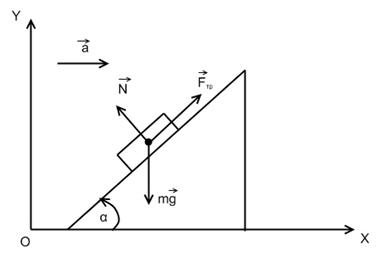
Рис. 2.5
Решение: Запишем второй закон Ньютона в проекциях на оси ОХ и ОY инерциальной системы отсчета, связанной с Землей, считая, что кубик относительно клина покоится:
![]() (1)
(1)
![]() (2)
(2)
Откуда
![]()
Так как кубик покоится относительно клина, то ![]() и
и ![]() связаны соотношением
связаны соотношением ![]() , т.е.
, т.е.
![]()
Откуда получим ![]() .
.
Следовательно, при ![]() кубик начнёт соскальзывать при ускорении клина, равном
кубик начнёт соскальзывать при ускорении клина, равном ![]() .
.
Если ![]() , то тело начнет соскальзывать при любом сколь угодно малом ускорении.
, то тело начнет соскальзывать при любом сколь угодно малом ускорении.
Заключение
При решении задач динамики нужно в первую очередь выбрать систему координат и задать начало отсчета времени.
Описание движения в различных системах координат эквивалентны между собой в том смысле, что при известном расположении двух систем координат относительно друг друга по величинам, найденным в первой системе, можно определить соответствующие величины во второй.
При решении задач следует выбрать такую систему координат, в которой уравнения, описывающие движение, получаются проще. При прямолинейном движении система уравнений получается проще, если одна из осей координат направлена вдоль движения.
При решении задач на движение нескольких тел рекомендуется пользоваться одной системой координат.
Список литературы
1. Калашников Н.П., Смондырев М.А.. Основы физики. Т.1. ![]() М.: Дрофа, 2003
М.: Дрофа, 2003
2. Калашников Н.П., Смондырев М.А. Основы физики. Упражнения и задачи. ![]() М.: Дрофа, 2004.
М.: Дрофа, 2004.
3. Чертов А.Г., Воробьев А.А. Задачник по физике. ![]() М.: Высш. шк., 1988.
М.: Высш. шк., 1988.
4. Новодворская Е.М., Дмитриев Э.М. Сборник задач по физике с решениями для втузов. ![]() М.: ООО Издательство «Мир и Образование», 2003.
М.: ООО Издательство «Мир и Образование», 2003.
5. Демков В.П., Третьякова О.Н. В помощь поступающим в ВУЗы. Физика. Механика. – М.: Издательство МАИ, 1996.
6. Касаткина И.Л. Репетитор по физике. Т.1. ![]() Ростов н/Д: Феникс, 2002.
Ростов н/Д: Феникс, 2002.
Похожие работы
... относительности (теории тяготения). Исходя из изложенного, в механике пользуются единым термином «масса», определяя массу как меру инертности тела и его гравитационных свойств. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ. РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ Для решения задач динамики точки будем пользоваться одной из следующих двух систем уравнений ...
... на определенный момент времени. В интервальном ряду динамики уровни ряда представлены за период времени. 1.2 Статистические методы анализа динамики объема производства продукции и услуг В статистическом изучении динамики объема производства продукции и услуг на предприятии можно использовать различные методы. Статистическое исследование динамического ряда объема производства продукции и ...
... будет показана эффективность применения в ряде случаев указанных способов. 1. О решении физических задач в средней школе 1.1 О возможности применения векторных многоугольников для решения физических задач Применение векторных способов, требующих знания основ тригонометрии (в частности, теорем синусов и косинусов), для решения задач механики в непрофильном 9 классе базовой школы вряд ли ...
... Фондовооружённость труда 2010,62 451,56 3561,88 22,46 177,15 Рентабельность общая, % 0,33 0,69 0,90 212,05 277,02 Рентабельность расчётная, % 0,23 0,48 0,66 204,98 282,73 2. Учет материально-производственных запасов на предприятии ОАО «АВТОВАЗАГРЕГАТ» 2.1 Организация и документальное оформление поступления и расхода материальных запасов Статьей 1 Федерального закона от ...
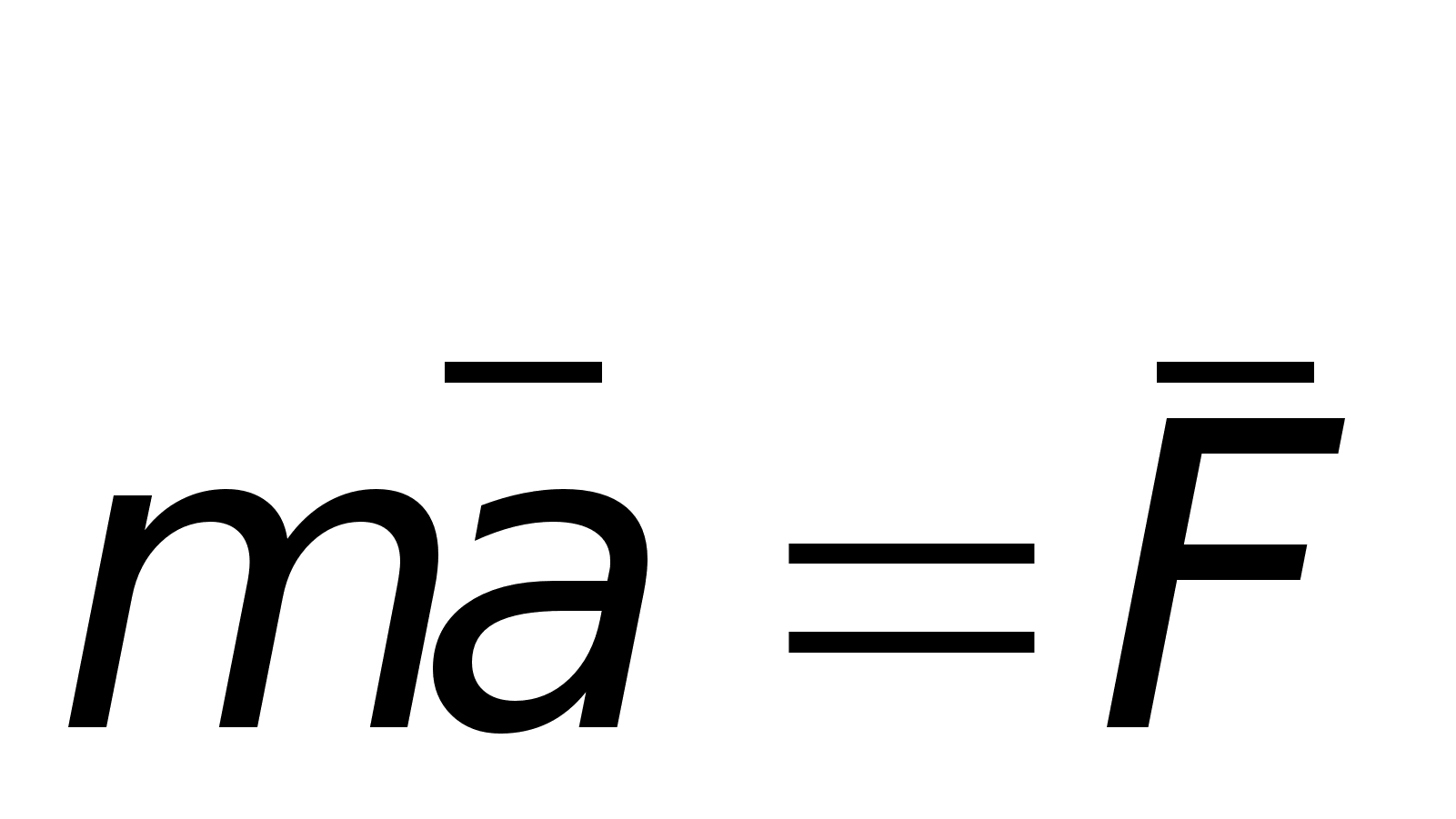
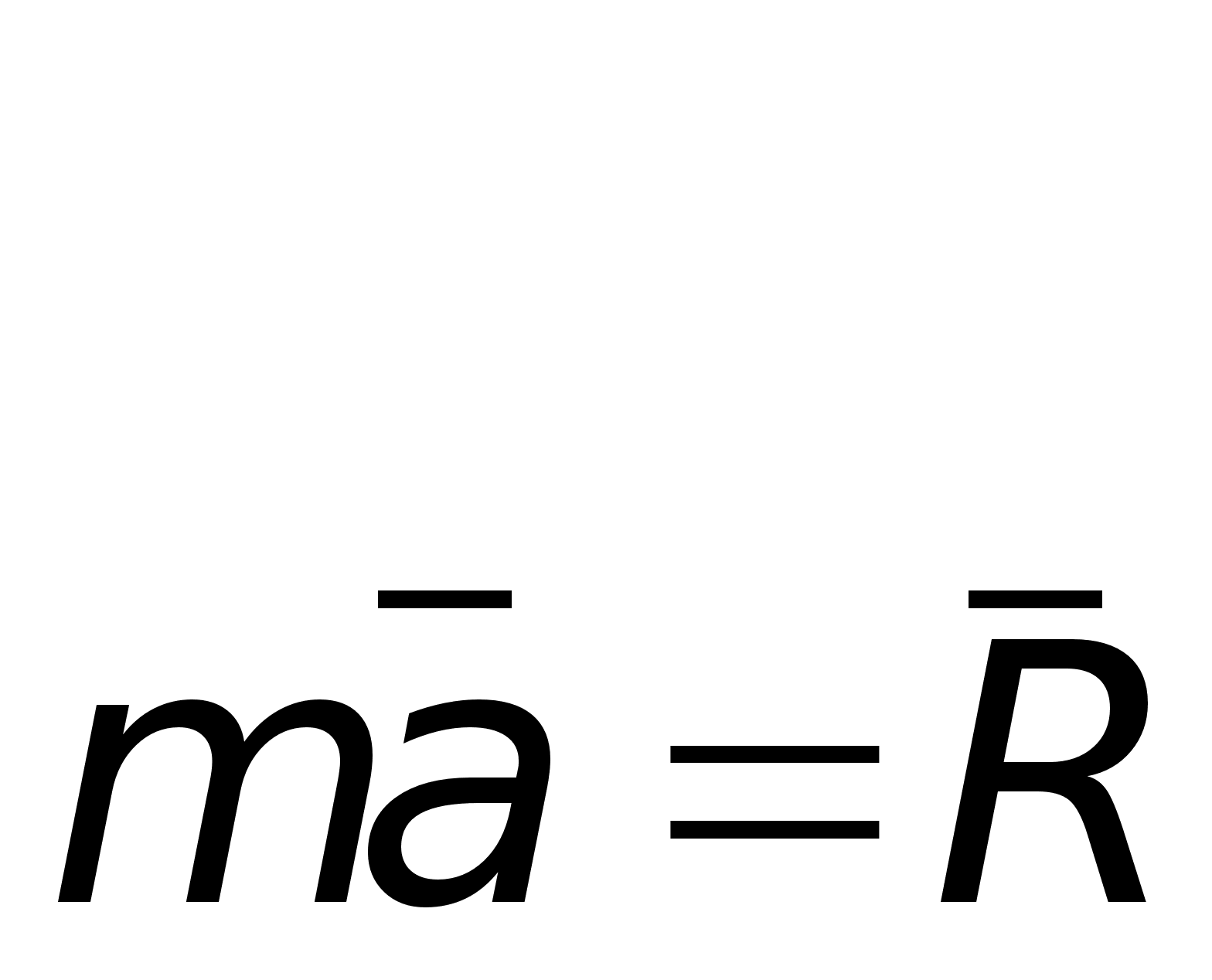
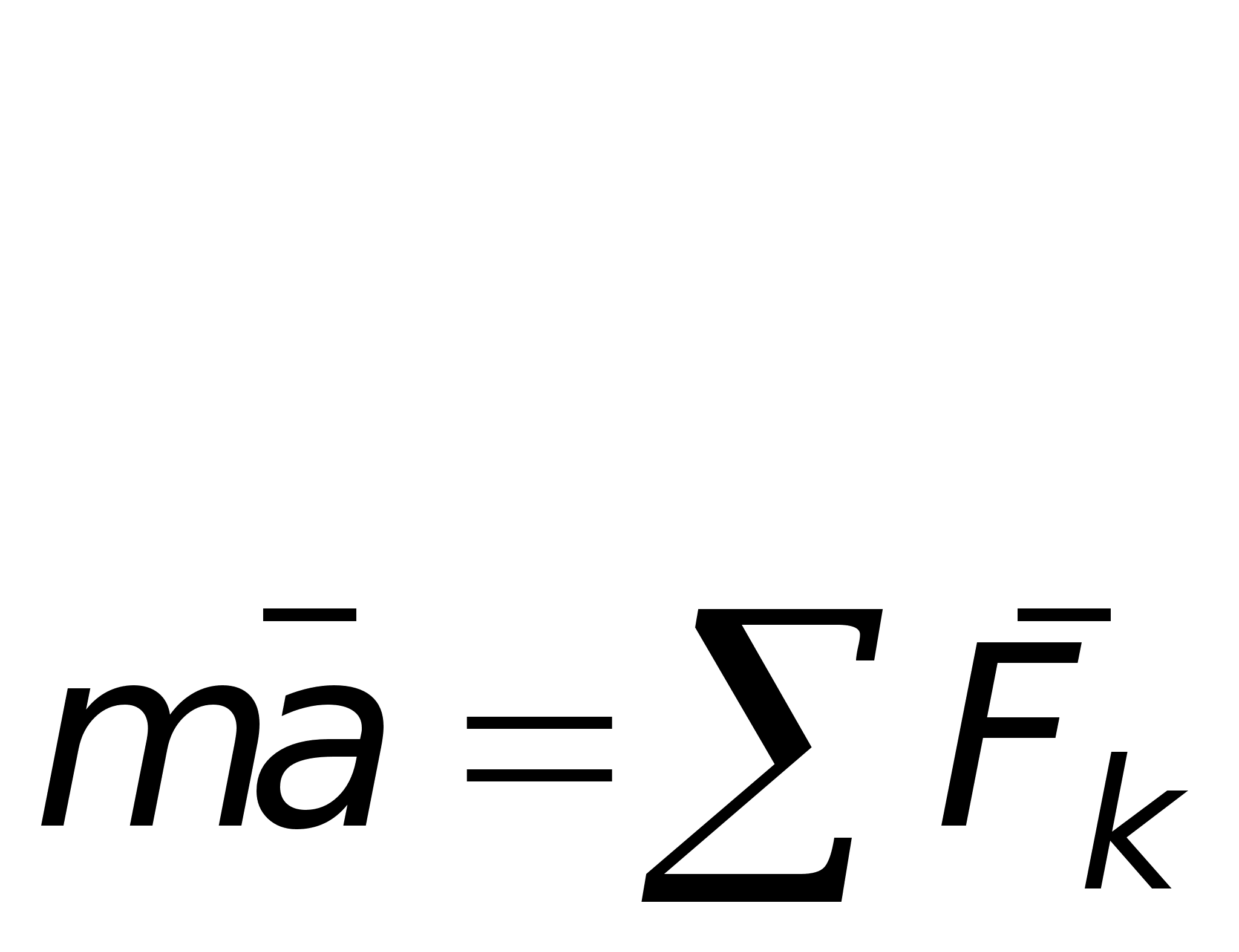



0 комментариев