Навигация
Равновесие жидкость—жидкость в двухкомпонентных системах
3.2 Равновесие жидкость—жидкость в двухкомпонентных системах
Растворы жидкостей в жидкостях очень разнообразны по твоей природе и свойствам. Растворимость жидкостей в жидкостях зависит от природы растворителя и растворенного вещества, температуры, присутствия в растворе посторонних веществ. Существуют растворы с неограниченной взаимной растворимостью, ограниченной взаимной растворимостью и с практически полной взаимной нерастворимостью жидкостей. Ограниченная взаимная растворимость двух жидкостей наблюдается в системах со значительным отклонением от идеальности. Растворимость таких жидкостей зависит от температуры. В одних системах взаимная растворимость жидкостей с ростом температуры увеличивается (системы с верхней критической температурой растворения), в других уменьшается (системы с нижней критической температурой растворения). Под критической температурой растворения понимают ту температуру, при которой составы двух равновесных жидких фаз одинаковы. Для изображения зависимости взаимной растворимости жидкостей от температуры при постоянном давлении строят диаграммы состояния в координатах температура—состав (диаграммы растворимости). При критической температуре растворения оба жидких раствора по составу тождественны, и является условно инвариантной (Сусл = 2 — 2 = 0). К системам с верхней критической температурой растворения относятся системы: вода—анилин, вода—фенол, вода—нитробензол. Иногда взаимная растворимость жидкостей увеличивается как с повышением, так и с понижением температуры (системы с верхней и нижней критическими температурами растворения). В некоторых системах критические температуры растворения не достигаются, так как при повышении температуры одна из жидкостей превращается в пар, а при понижении температуры одна из жидкостей кристаллизуется.
3.3 Равновесие пар—жидкий раствор в двухкомпонентных системах
3.3.1 Равновесие пар—жидкий раствор в системах с неограниченной взаимной растворимостью жидкостей
Если раствор образован из двух летучих, неограниченно растворимых друг в друге жидкостей, то пар, находящийся в равновесии с жидким раствором, будет содержать оба компонента. В общем случае состав пара отличается от состава жидкого раствора, из которого он получен. При невысоких давлениях пар можно рассматривать как смесь идеальных газов. Если пар подчиняется законам идеальных газов и находится в равновесии с идеальным раствором, то состав паровой фазы легко найти, зная состав жидкой фазы. Согласно закону Дальтона общее давление пара над идеальным раствором равно сумме парциальных давлений пара компонентов:
![]() (9)
(9)
Во всем интервале концентраций идеального жидкого раствора растворитель и растворенное вещество подчиняются закону Рауля:
![]() (10)
(10)
Для бинарного раствора, исходя из (9) и (10),
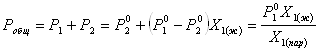 (11)
(11)
отсюда после некоторых преобразований имеем
![]()
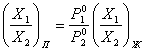 (12)
(12)
Из уравнения (12) следует, что только при равенстве давлений пара над чистыми компонентами ![]() ) состав пара одинаков с составом жидкого раствора, из которого он получен. Во всех остальных случаях, даже для идеальных растворов, состав пара отличается от состава исходного раствора.
) состав пара одинаков с составом жидкого раствора, из которого он получен. Во всех остальных случаях, даже для идеальных растворов, состав пара отличается от состава исходного раствора.
Среди реально существующих растворов имеется много таких систем, для которых уравнение (12) позволяет рассчитать состав пара заданном составе жидкого раствора.
На практике чаще приходится встречаться с неидеальными растворами, которые не подчиняются закону Рауля. В этих случаях состав пара определяется опытным путем. Для изучения равновесия пар— жидкий раствор применяют два типа диаграмм состояния:
диаграммы давление пара — состав (Т — const)
диаграммы температура кипения – состав (Р – const)
На практике для изучения равновесия пар – жидкий раствор, чаще используются диаграммы температура—состав (диаграммы кипения). Реальные растворы со значительным положительным или отрицательным отклонением от идеальности способны образовывать азеотропные смеси (азеотропы), которые на диаграммах состояния. Азеотропные смеси — это растворы, при испарении которых получается пар того же состава, что и исходная жидкая смесь![]() . Азеотропные смеси—условно инвариантные системы (Сусл = 2 — 2 = 0). В реальных растворах азеотропная смесь имеет самую низкую или самую высокую температуру кипения. При изменении внешнего давления изменяется не только температура кипения, но и состав азеотропного раствора. Это указывает на то, что азеотропная смесь не является химическим соединением. Как для идеальных, так и для реальных растворов справедлив первый закон Гиббса—Коновалова: пар по сравнению с жидким раствором, из которого он получен, при равновесии богаче тем компонентом, прибавление которого к раствору приводит к понижению температуры кипения раствора при заданном внешнем давлении или к повышению давления пара над раствором. В системах с азеотропными смесями добавление к раствору более летучего компонента не всегда приводит к повышению давления пара над раствором, т.е. к понижению температуры кипения раствора. Для реальных растворов с азеотропными смесями справедлив также второй закон Гиббса—Коновалова: в азеотропных смесях, составы жидкости и пара совпадают. Азеотропные смеси образуются не только в системах со значительными отклонениями от закона Рауля, но и в системах с незначительными отклонениями, когда компоненты раствора имеют близкие температуры кипения, т.е. почти одинаковые давления пара над чистыми компонентами
. Азеотропные смеси—условно инвариантные системы (Сусл = 2 — 2 = 0). В реальных растворах азеотропная смесь имеет самую низкую или самую высокую температуру кипения. При изменении внешнего давления изменяется не только температура кипения, но и состав азеотропного раствора. Это указывает на то, что азеотропная смесь не является химическим соединением. Как для идеальных, так и для реальных растворов справедлив первый закон Гиббса—Коновалова: пар по сравнению с жидким раствором, из которого он получен, при равновесии богаче тем компонентом, прибавление которого к раствору приводит к понижению температуры кипения раствора при заданном внешнем давлении или к повышению давления пара над раствором. В системах с азеотропными смесями добавление к раствору более летучего компонента не всегда приводит к повышению давления пара над раствором, т.е. к понижению температуры кипения раствора. Для реальных растворов с азеотропными смесями справедлив также второй закон Гиббса—Коновалова: в азеотропных смесях, составы жидкости и пара совпадают. Азеотропные смеси образуются не только в системах со значительными отклонениями от закона Рауля, но и в системах с незначительными отклонениями, когда компоненты раствора имеют близкие температуры кипения, т.е. почти одинаковые давления пара над чистыми компонентами ![]() . В этом случае на диаграмме состояния появляется экстремум, лежащий в средней части диаграммы. Чем больше различие между
. В этом случае на диаграмме состояния появляется экстремум, лежащий в средней части диаграммы. Чем больше различие между ![]() и
и ![]() , тем больше положение экстремума сдвинуто в сторону одного из компонентов системы: при максимуме на кривой давления пара в сторону более летучего компонента, при минимуме — в сторону менее летучего компонента.
, тем больше положение экстремума сдвинуто в сторону одного из компонентов системы: при максимуме на кривой давления пара в сторону более летучего компонента, при минимуме — в сторону менее летучего компонента.
Похожие работы
... MnY2S4 и фазы MgLn4S7 моноклинной сингонии. Условие существования фаз, характер плавления не известны. Ограниченность и неполнота литературных данных определяет актуальность задачи изучения фазовых равновесий в системе MgS – Y2S3. Глава 2. Методическая часть. 2.1. Методы физико-химического анализа Исходя из свойств полуторных сульфидов, таких, как термическая стабильность, летучесть, и ...
... Точками области 1 соответствует газообразное, области 2 - жидкое, области 3 - твердое состояние вещества. Плоскость ТР с указанными тремя кривыми равновесия называется диаграммой состояния. Диаграмма состояния позволяет судить, какие будут происходить фазовые превращения при том или ином процессе. Допустим, например, что производится нагревание при постоянном давлении. На диаграмме состояния такой ...
... равны удельным значениям энтропии, взятой с обратным знаком, и объеме: (4.30) Если в точках, удовлетворяющих фазовому равновесию: , первые производные химического потенциала для разных фаз испытывают разрыв: , (4.31) говорят, что термодинамическая система испытывает фазовый переход I-го рода. Для фазовых переходов первого рода характерно наличие срытой теплоты фазового перехода, ...
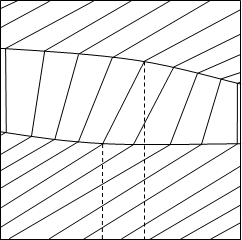
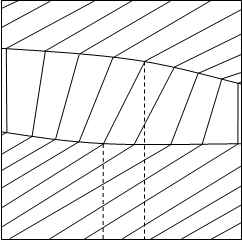
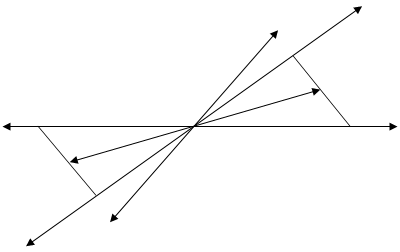
... как в азеотропных смесях коннода вертикальна, нода вырождается в точку. 3. Фазовые эффекты и уравнение Ван-дер-Ваальса для бинарных азеотропных смесей. Фазовые эффекты в бинарных азеотропных смесях. На рисунках 3.1 - 3.4 изображены диаграммы объем - состав фаз, и энтропия – состав фаз для азеотропа с минимумом температуры кипения. Если рассматриваемый состав равен составу ...

0 комментариев