Навигация
4. Уравнение Клапейрона
Термодинамическое обоснование эмпирических соотношений между давлением равновесного пара и температуре было дано Клапейроном в 1834 г. Рассмотрим жидкость, находящуюся в равновесии с ее паром при температуре Т и давлении, равном давлении равновесного пара Р при этой температуре.
Термодинамическим критерием равновесия при постоянных температуре и давлении является равенство изобарных потенциалов для этих двух состояний:
![]() , (16)
, (16)
где «ж» и «пар» — индексы, обозначающие жидкость и пар.
Если температура повысилась до Т+dТ, то для того чтобы обе фазы остались в равновесии, давление должно увеличиться до Р+dР, равного давлению пара при этой более высокой температуре. При бесконечно малом повышении температуры и давления изобарный потенциал для жидкости станет равным G(ж)+dG(ж), а для пара G(пар)+dG(пар). Так как обе фазы находятся в равновесии, то
![]() (17)
(17)
С учетом уравнения (16) условие сохранения равновесия при изменении температуры и давления имеет вид:
![]() (18)
(18)
Так как dG представляет собой полный дифференциал, то уравнение (18) можно написать следующим образом:
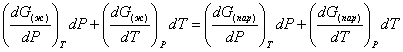 (19)
(19)
На основании уравнений ![]() и
и ![]() уравнение (19) можно переписать в виде
уравнение (19) можно переписать в виде
![]() (20)
(20)
При подстановке получим
![]() (21)
(21)
Так как по уравнению
![]()
![]()
![]() (22)
(22)
где ![]() — изменение энтальпии при испарении жидкости при температуре Т, то уравнение (21) можно написать следующим образом:
— изменение энтальпии при испарении жидкости при температуре Т, то уравнение (21) можно написать следующим образом:
![]() (23)
(23)
Это важное соотношение известно как уравнение Клапейрона. Оно дает зависимость скорости изменения давления равновесного пара с температурой (dР/dТ) от энтальпии испарения ![]() , объема жидкости V (ж) и объема пара V(пар) при температуре Т и давлении, равном давлению насыщенного пара. Вследствие того что вывод уравнения (23) не зависит от каких-либо предположений относительно природы обеих фаз, можно легко вывести такие же уравнения для равновесия между твердым веществом и паром, находящимся в равновесии с ним, а также для равновесия между твердым веществом и жидкостью и между двумя различными кристаллическими формами твердого вещества. Для этих случаев уравнение (23) можно написать так:
, объема жидкости V (ж) и объема пара V(пар) при температуре Т и давлении, равном давлению насыщенного пара. Вследствие того что вывод уравнения (23) не зависит от каких-либо предположений относительно природы обеих фаз, можно легко вывести такие же уравнения для равновесия между твердым веществом и паром, находящимся в равновесии с ним, а также для равновесия между твердым веществом и жидкостью и между двумя различными кристаллическими формами твердого вещества. Для этих случаев уравнение (23) можно написать так:
![]() (24)
(24)
![]()
![]() (25)
(25)
 (26)
(26)
где ![]() ,
, ![]() и
и ![]() — энтальпии возгонки, плавления и перехода (между твердым состоянием 1 и 2) соответственно. Теплоты возгонки, плавления и испарения при заданной температуре связаны соотношением
— энтальпии возгонки, плавления и перехода (между твердым состоянием 1 и 2) соответственно. Теплоты возгонки, плавления и испарения при заданной температуре связаны соотношением
![]() (27)
(27)
поскольку количество тепла, необходимое для испарения данного количества твердого вещества, остается постоянным, независимо от того, проводится ли процесс испарения твердого вещества непосредственно или путем первоначального плавления твердого вещества с последующим испарением жидкости. Каждое из этих уравнений можно выразить через мольные величины.
При пользовании уравнениями (23) — (26) необходимо выражать изменение энтальпии процесса в тех же единицах, что и произведение давления на изменение объема. Для этой цели полезно рассчитать множитель для перевода кал в л • атм:
![]()
5. Уравнение Клаузиуса — Клапейрона
Клаузиус показал, как можно упростить уравнение Клапейрона для случаев испарения и возгонки, исходя из предположения, что пар подчиняется закону идеального газа и что мольным объемом жидкости ![]() (ж) по сравнению с мольным объемом пара
(ж) по сравнению с мольным объемом пара ![]() (пар) можно пренебречь. Например, для воды при 100° V(пар) =30.2 л а V(ж)=0,0188 л. Подставляя RT/Р вместо V (пар), получим
(пар) можно пренебречь. Например, для воды при 100° V(пар) =30.2 л а V(ж)=0,0188 л. Подставляя RT/Р вместо V (пар), получим
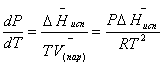 (28)
(28)
После преобразования выражение принимает вид:
![]() (29)
(29)
![]() (30)
(30)
Интегрирование в предположении, что ![]() не зависит от температуры, дает:
не зависит от температуры, дает:
![]() (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
где С — константа интегрирования.
Теперь очевидна теоретическая основа эмпирического соотношения ![]() . Уравнение (32) представляет собой уравнение прямой линии, если рассматривать lnР как функцию
. Уравнение (32) представляет собой уравнение прямой линии, если рассматривать lnР как функцию ![]() . Тангенс угла наклона прямой равен
. Тангенс угла наклона прямой равен ![]() а при использовании десятичных логарифмов он равен
а при использовании десятичных логарифмов он равен ![]() . Таким образом, теплоту испарения можно рассчитать с применением выражения
. Таким образом, теплоту испарения можно рассчитать с применением выражения
![]()
![]()
![]()
![]() (34)
(34)
Часто удобнее пользоваться уравнением, полученным при интегрировании в пределах Р2, Т2 и Р1, Т1:
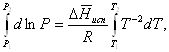 (35)
(35)
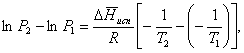 (36)
(36)
![]() (37)
(37)
По этому уравнению можно рассчитать теплоту испарения, исходя из давления равновесного пара при двух различных температурах; если известны теплота испарения и давление пара при одной температуре, можно рассчитать давление пара при другой температуре при условии, что ![]() остается постоянной. Давление можно выразить в любых единицах, но эти единицы должны быть одинаковыми для обоих давлений. Точно так же можно выбрать любые единицы энергии при условии, что
остается постоянной. Давление можно выразить в любых единицах, но эти единицы должны быть одинаковыми для обоих давлений. Точно так же можно выбрать любые единицы энергии при условии, что![]() и R будут выражены в одинаковых единицах. Изменение давления пара твердого вещества с температурой можно выразить с помощью уравнения (37) при условии, что температурный интервал не слишком широк. Вследствие того, что теплота возгонки твердого вещества больше, чем теплота испарения соответствующей жидкости, давление пара твердого вещества быстрее изменяется с температурой, чем давление пара соответствующей жидкости, и кривая идет круче. Дифференциальное выражение (28) можно применять, если изменения температуры и давления малы. Например, удобно пользоваться следующей формулой для внесения поправок в температуру кипения при колебаниях атмосферного давления:
и R будут выражены в одинаковых единицах. Изменение давления пара твердого вещества с температурой можно выразить с помощью уравнения (37) при условии, что температурный интервал не слишком широк. Вследствие того, что теплота возгонки твердого вещества больше, чем теплота испарения соответствующей жидкости, давление пара твердого вещества быстрее изменяется с температурой, чем давление пара соответствующей жидкости, и кривая идет круче. Дифференциальное выражение (28) можно применять, если изменения температуры и давления малы. Например, удобно пользоваться следующей формулой для внесения поправок в температуру кипения при колебаниях атмосферного давления:
![]() (38)
(38)
Так как уравнение (37) для расчета теплоты испарения выведено в предположении, что пар есть идеальный газ, то результаты, получаемые при пользовании этим уравнением, не более точны, чем расчеты, в которые входит уравнение ![]() .
.
Другое приближение содержит допущение о том, что теплота испарения не зависит от температуры. Однако в широком интервале температур графики зависимости lgP от 1/Т несколько искривлены, потому что ![]() меняется с температурой. В этом случае можно рассчитать теплоту испарения для какой-нибудь определенной температуры из наклона кривой путем проведения касательной к этой кривой при заданной температуре. Уравнение для давления равновесного пара, которое дает линейное изменение
меняется с температурой. В этом случае можно рассчитать теплоту испарения для какой-нибудь определенной температуры из наклона кривой путем проведения касательной к этой кривой при заданной температуре. Уравнение для давления равновесного пара, которое дает линейное изменение ![]() с температурой, можно вывести следующим образом. Согласно уравнению
с температурой, можно вывести следующим образом. Согласно уравнению ![]() зависимость мольной теплоты испарения
зависимость мольной теплоты испарения ![]() от температуры выражается уравнением
от температуры выражается уравнением
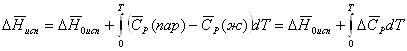 (39)
(39)
где ![]() - гипотетическая теплота испарения при абсолютном нуле. В предположении, что
- гипотетическая теплота испарения при абсолютном нуле. В предположении, что ![]() не зависит от температуры,
не зависит от температуры,
![]()
Так как разность ![]() отрицательна,
отрицательна, ![]() уменьшается по мере повышения температуры. Именно этого можно было ожидать на основании молекулярно-кинетических представлений, потому что жидкость с повышением температуры расширяется, вследствие этого расстояние между молекулами увеличивается и для их отрыва при образовании пара требуется меньше энергии.
уменьшается по мере повышения температуры. Именно этого можно было ожидать на основании молекулярно-кинетических представлений, потому что жидкость с повышением температуры расширяется, вследствие этого расстояние между молекулами увеличивается и для их отрыва при образовании пара требуется меньше энергии.
Подставляя ![]() в уравнение (30), получим
в уравнение (30), получим
![]()
![]() (40)
(40)
Тогда неопределенный интеграл этого выражения равен:
![]() (41)
(41)
![]() (42)
(42)
Для определения трех констант А,В,С нужно решить систему из трех уравнений, при составлении которой необходимы точные данные при трех температурах. Уравнение (42) применимо в более широком интервале температур, чем уравнение (32), однако и оно не является точным, поскольку отклонение свойств пара от свойств идеального газа приводит к заметной ошибке, которая не учитывается при выводе уравнения.
Похожие работы
... MnY2S4 и фазы MgLn4S7 моноклинной сингонии. Условие существования фаз, характер плавления не известны. Ограниченность и неполнота литературных данных определяет актуальность задачи изучения фазовых равновесий в системе MgS – Y2S3. Глава 2. Методическая часть. 2.1. Методы физико-химического анализа Исходя из свойств полуторных сульфидов, таких, как термическая стабильность, летучесть, и ...
... Точками области 1 соответствует газообразное, области 2 - жидкое, области 3 - твердое состояние вещества. Плоскость ТР с указанными тремя кривыми равновесия называется диаграммой состояния. Диаграмма состояния позволяет судить, какие будут происходить фазовые превращения при том или ином процессе. Допустим, например, что производится нагревание при постоянном давлении. На диаграмме состояния такой ...
... равны удельным значениям энтропии, взятой с обратным знаком, и объеме: (4.30) Если в точках, удовлетворяющих фазовому равновесию: , первые производные химического потенциала для разных фаз испытывают разрыв: , (4.31) говорят, что термодинамическая система испытывает фазовый переход I-го рода. Для фазовых переходов первого рода характерно наличие срытой теплоты фазового перехода, ...
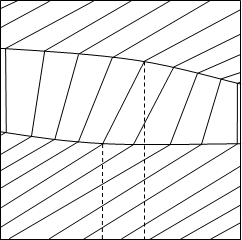
... как в азеотропных смесях коннода вертикальна, нода вырождается в точку. 3. Фазовые эффекты и уравнение Ван-дер-Ваальса для бинарных азеотропных смесей. Фазовые эффекты в бинарных азеотропных смесях. На рисунках 3.1 - 3.4 изображены диаграммы объем - состав фаз, и энтропия – состав фаз для азеотропа с минимумом температуры кипения. Если рассматриваемый состав равен составу ...
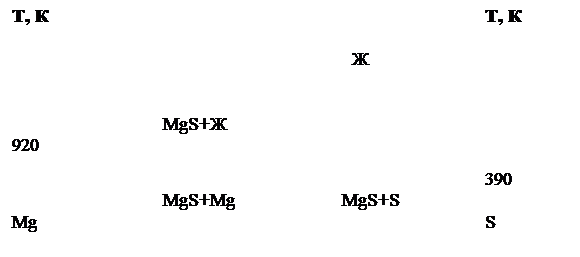

0 комментариев