Найпоширенішою задачею в теорії звичайних рівнянь є задача Коші. Додаткові умови цієї задачі за своєю суттю є початковими: в них фігурують значення невідомої функції та її похідних( якщо порядок рівняння перевищує одиницю) при фіксованому значенні незалежної змінної. Зрозуміло, що це не єдиний спосіб виділення того, чи іншого частинного розв’язку з множини всіх функцій, які задовольняють диференціальне рівняння. Часто виникає потреба у знаходженні такого розв’язку, для якого виконувалися б так звані крайові умови: значення шуканої функції та її похідних мають задовольняти певні співвідношення в кількох фіксованих точках проміжку, який пробігає незалежна змінна. Причому, задачу відшукання такого розв’язку називають крайовою задачею. Такі крайові задачі мають прикладне значення і частіше виникають у практиці. Наприклад,задача про форму провислого каната із закріпленими кінцями зводиться до відшукання такого розв’язку диференціального рівняння другого порядку, графік якого проходив би через дві наперед задані точки, або, щоб знайти Т-періодичний розв'язок лінійного Т-періодичного рівняння ![]() , потрібно з усіх розв’язків вибрати той, який задовольняє умову
, потрібно з усіх розв’язків вибрати той, який задовольняє умову ![]() . Для розв’язання крайових задач використовують так звану функцію Гріна, спробуємо зрозуміти, як вона будується у загальному випадку.
. Для розв’язання крайових задач використовують так звану функцію Гріна, спробуємо зрозуміти, як вона будується у загальному випадку.
Розглянемо випадок,коли однорідна крайова задача
![]() (1)
(1)
![]()
![]() (2),
(2),
має хоча б один нетривіальний розв’язок. При цьому, нехай функція ![]() неперервно диференційована на
неперервно диференційована на ![]() , а дійсні функції
, а дійсні функції ![]() - неперервні на
- неперервні на ![]() ,та
,та ![]() - задані числа, причому,
- задані числа, причому,![]()
![]()
Позначимо цей розв’язок через ![]() .
.
Твердження 1.
Однорідна крайова задача (1),(2) має нетривіальний розв'язок тоді і лише тоді, коли розв’язки ![]() та
та ![]() лінійно залежні.
лінійно залежні.
Доведення.
Нехай неоднорідна крайова задача має нетривіальний розв'язок ![]() . Оскільки як
. Оскільки як ![]() , так і
, так і ![]() задовольняють першу крайову умову (2), а
задовольняють першу крайову умову (2), а ![]() , то вронскіан цих розв’язків дорівнює нулю, а отже, вони лінійно залежні. Так само можна довести лінійну залежність розв’язків
, то вронскіан цих розв’язків дорівнює нулю, а отже, вони лінійно залежні. Так само можна довести лінійну залежність розв’язків ![]() та
та ![]() . Звідси випливає, що
. Звідси випливає, що ![]() та
та ![]() також лінійно залежні.
також лінійно залежні.
Навпаки,нехай зазначені розв’язки лінійно залежні. Тоді для деякої сталої ![]() маємо
маємо ![]() . Тепер зрозуміло,що, наприклад, функція
. Тепер зрозуміло,що, наприклад, функція ![]() :=
:=![]() є розв’язком однорідної крайової задачі. Твердження доведено.
є розв’язком однорідної крайової задачі. Твердження доведено.
Звідси можна зробити висновок, що множина всіх розв’язків задачі – це сім’я функцій вигляду, ![]() , де
, де ![]() - довільна стала. Тому, не обмежуючи загальності викладу, вважатимемо, що
- довільна стала. Тому, не обмежуючи загальності викладу, вважатимемо, що ![]() вибрано так, щоб справджувалась умова нормування
вибрано так, щоб справджувалась умова нормування
![]()
Необхідну умову існування розв’язку неоднорідної крайової задачі встановлює таке твердження.
Твердження 2.
Якщо задача
![]() (3)
(3)
![]()
![]() (2)
(2)
Має розв’язок ![]() , то функція ортогональна до нетривіального розв’язку
, то функція ортогональна до нетривіального розв’язку ![]() відповідної крайової задачі (1),(2), тобто
відповідної крайової задачі (1),(2), тобто
![]() (4)
(4)
Доведення.
Застосуємо формулу Гріна до пари функцій ![]() та
та ![]() . Оскільки вони задовольняють крайові умови то згідно з властивістю симетричності оператора
. Оскільки вони задовольняють крайові умови то згідно з властивістю симетричності оператора ![]() маємо:
маємо:
![]()
Урахувавши, що ![]() і
і ![]() , дістанемо (4). Зауважимо, що при довільному
, дістанемо (4). Зауважимо, що при довільному ![]() функція
функція ![]() теж є розв’язком задачі (3),(2). Аби уникнути такої неоднозначності, умови (2) слід доповнити ще однією. Найприроднішою додатковою умовою є вимога ортогональності
теж є розв’язком задачі (3),(2). Аби уникнути такої неоднозначності, умови (2) слід доповнити ще однією. Найприроднішою додатковою умовою є вимога ортогональності
![]() (5)
(5)
Твердження 3.
Якщо задача (3),(2),(5) має розв’язок ![]() ,то він єдиний.
,то він єдиний.
Доведення.
Справді, різниця двох розв’язків задачі (3),(2),(5) є розв’язком вигляду ![]() відповідної однорідної задачі. З умови (5) та нормованості функції
відповідної однорідної задачі. З умови (5) та нормованості функції ![]() одразу випливає, що
одразу випливає, що
![]()
Розв’яжемо вироджену крайову задачу за допомогою методу варіації довільних сталих, вважаючи, що умова ортогональності (4) справджується. Виберемо лінійно незалежний з ![]() розв’язок
розв’язок ![]() однорідного рівняння (1) так, щоб виконувалася рівність
однорідного рівняння (1) так, щоб виконувалася рівність
![]()
Цим ми дещо спростимо формули, які буде одержано нижче. Шукаємо розв’язок (3) методом варіації сталих у вигляді
![]() (6)
(6)
отримаємо таку систему:
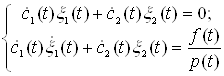
Розв’яжемо її відносно ![]() та
та ![]() за правилом Крамера.
за правилом Крамера.
Маємо рівняння
![]() ,
,![]() (7)
(7)
При цьому
![]()
![]()
Тому, аби розв’язок ![]() задовольняв крайову умову в точці
задовольняв крайову умову в точці ![]() ,необхідно вимагати виконання рівності
,необхідно вимагати виконання рівності ![]() . Звідси
. Звідси ![]() і з урахуванням (4)
і з урахуванням (4) ![]() . Остання рівність забезпечить справдження крайової умови в правому кінці проміжку
. Остання рівність забезпечить справдження крайової умови в правому кінці проміжку ![]() .
.
Загальний розв’язок першого з рівнянь (7) візьмемо у вигляді 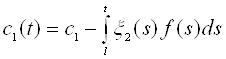 , де
, де ![]() - довільна стала. Підставивши знайдені функції
- довільна стала. Підставивши знайдені функції ![]() ,
,![]() в (6), дістанемо одно параметричну сім’ю функцій
в (6), дістанемо одно параметричну сім’ю функцій
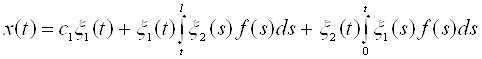 , (8)
, (8)
Кожна з яких є розв’язком крайової задачі (3),(2). Умову ортогональності (5) завжди можна задовольнити, відповідним чином обравши довільну сталу с1.
Підсумком наведених міркувань є така теорема:
Теорема1
Розв’язок крайової задачі (3) (2) існує тоді і лише тоді, коли функція ![]() ортогональна до кожного розв'язку відповідної однорідної крайової задачі.
ортогональна до кожного розв'язку відповідної однорідної крайової задачі.
Тепер покажемо, що розв’язок(8) можна подати у вигляді інтегрального перетворення
![]() ,
,
Де функція ![]() задовольняє крайові умови й при кожному
задовольняє крайові умови й при кожному ![]()
є ортогональною до ![]() .
.
Насамперед, запровадивши функцію
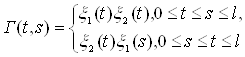
за аналогією з не виродженим випадком, перепишемо (8) у вигляді
![]() (9)
(9)
Оскільки ![]() ,
,![]()
![]() ,
,
![]() ,
, ![]() ,
,
То ![]() задовольняє умову лише в лівому кінці проміжку
задовольняє умову лише в лівому кінці проміжку ![]() , адже розв’язок
, адже розв’язок ![]() не задовольняє жодної умови (2). Отже, функцію
не задовольняє жодної умови (2). Отже, функцію ![]() доведеться відповідним чином виправити. Для цього звернемо увагу на такий факт:якщо у формулі(9) зробити заміну
доведеться відповідним чином виправити. Для цього звернемо увагу на такий факт:якщо у формулі(9) зробити заміну ![]()
![]()
![]() -
-![]() , де
, де ![]() довільні функції, то вона й надалі визначатиме розв’язок рівняння (3):адже
довільні функції, то вона й надалі визначатиме розв’язок рівняння (3):адже ![]() ортогональна до
ортогональна до ![]() . Неважко зрозуміти, що перетворена функція
. Неважко зрозуміти, що перетворена функція ![]() задовольнятиме обидві крайові умови, якщо функцію
задовольнятиме обидві крайові умови, якщо функцію ![]() вибрати так, щоб при деякому
вибрати так, щоб при деякому ![]() виконувалися рівності
виконувалися рівності
![]() ,
,![]() ,
,![]() ,
,![]() (10)
(10)
Найзручнішим буде такий вибір:
![]()
![]()
Легко перевірити, що ця функція не лише задовольняє умови (10), а й є розв’язком неоднорідного рівняння ![]() =
= ![]() . При цьому, якщо додатково вимагати, аби розв'язок
. При цьому, якщо додатково вимагати, аби розв'язок ![]() був ортогональним до
був ортогональним до ![]() на
на ![]() ,то
,то ![]() .
.
Тепер залишилось покласти
![]()
І вибрати функцію ![]() так, щоб
так, щоб ![]() була ортогональною до
була ортогональною до ![]() . Для цього домножимо праву частину останньої нерівності на
. Для цього домножимо праву частину останньої нерівності на ![]() , одержаний добуток зінтегруємо за змінною
, одержаний добуток зінтегруємо за змінною ![]() і результат прирівняємо до нуля. З одержаного рівняння легко знайдемо
і результат прирівняємо до нуля. З одержаного рівняння легко знайдемо
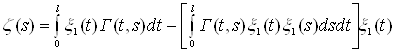 .
.
Остаточно маємо
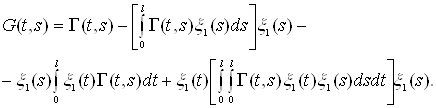 (11)
(11)
З урахуванням властивостей цієї функції дамо таке означення.
Означення.
Функцію ![]() називатимемо узагальненою функцією Гріна крайової задачі (2)-(3), якщо вона задовольняє такі умови:
називатимемо узагальненою функцією Гріна крайової задачі (2)-(3), якщо вона задовольняє такі умови:
1. Функція ![]() неперервна в квадраті К=
неперервна в квадраті К=![]() ,має неперервні частинні похідні
,має неперервні частинні похідні ![]() ,
,![]() у кожному з трикутників
у кожному з трикутників ![]() ,
,![]() ;
;
2. Для кожного фіксованого ![]() функція
функція ![]() задовольняє рівняння Lx(t)= -
задовольняє рівняння Lx(t)= -![]()
![]() при всіх
при всіх ![]() ,
,![]() , а також крайовій умові (2).
, а також крайовій умові (2).
3. На діагоналі ![]() квадрата К похідна
квадрата К похідна ![]() має розрив першого роду зі стрибком 1/p(s):
має розрив першого роду зі стрибком 1/p(s): ![]() -
-![]() .
.
4. Для кожного фіксованого ![]() функція
функція![]() ортогональна до функції
ортогональна до функції ![]() :
: ![]() .
.
5.
Сформулюємо алгоритм відшукання узагальненої функції Гріна.
· Знаходимо таку фундаментальну систему ![]() ,
,![]() лінійного однорідного рівняння (1), щоб розв'язок
лінійного однорідного рівняння (1), щоб розв'язок ![]() задовольняв умови(2).
задовольняв умови(2).
· Знаходимо будь-який розв'язок g(t,s) неоднорідного рівняння Lx(t)= -![]()
![]() .
.
· Узагальнену функцію Гріна шукаємо у вигляді
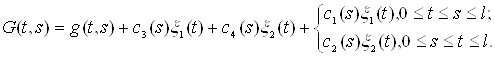
Функції ![]() обираємо так, щоб останній доданок задовольняв пунктам 1 і 3 означення узагальненої функції Гріна;функцію
обираємо так, щоб останній доданок задовольняв пунктам 1 і 3 означення узагальненої функції Гріна;функцію ![]() - так, щоб
- так, щоб ![]() задовольняла крайові умови задачі;нарешті, вибором функції
задовольняла крайові умови задачі;нарешті, вибором функції ![]() забезпечуємо виконання умови ортогональності 4.
забезпечуємо виконання умови ортогональності 4.
Проаналізувавши вигляд правої частини формули (11), можна зробити висновок, що ![]() з потрібними властивостями існують.
з потрібними властивостями існують.
Розглянемо приклад.
Розв’яжемо крайову задачу
![]() ,
, ![]() <
<![]() <
< ![]() ;
;
![]()
Розв'яжемо відповідне однорідне рівняння ![]() , застосувавши метод Ейлера. Тобто розв'язок
, застосувавши метод Ейлера. Тобто розв'язок ![]() шукаємо у вигляді
шукаємо у вигляді![]() =
= ![]() . Знайшовши
. Знайшовши
![]() =
=![]() ,
,![]() =
=![]() , підставивши ці значення в рівняння та скоротивши на
, підставивши ці значення в рівняння та скоротивши на ![]() маємо так зване характеристичне рівняння:
маємо так зване характеристичне рівняння:![]() ,з якого знайдемо корені
,з якого знайдемо корені ![]() :
: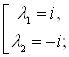
З цього маємо фундаментальну систему розв’язків рівняння:
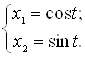
За теоремою про загальний розв'язок однорідного рівняння, маємо:
![]() де
де ![]()
Тому можемо сказати, що відповідна однорідна задача має однопараметричну сім’ю розв’язків ![]() , де
, де ![]() – довільна стала, для якої умова теореми 1 виконано, бо
– довільна стала, для якої умова теореми 1 виконано, бо 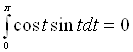 . Методом невизначених коефіцієнтів знайдемо частинний розв’язок диференціального рівняння задачі:
. Методом невизначених коефіцієнтів знайдемо частинний розв’язок диференціального рівняння задачі: ![]() . Загальний розв’язок цього рівняння має вигляд:
. Загальний розв’язок цього рівняння має вигляд:
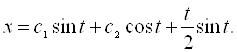
Для того, щоб задовольнити крайовій умові, достатньо покласти ![]() . Сталу
. Сталу ![]() виберемо так, щоб справджувалась умова ортогональності шуканого розв’язку й функції
виберемо так, щоб справджувалась умова ортогональності шуканого розв’язку й функції ![]() :
:
![]()
Звідси ![]() =
=![]() . Остаточно маємо:
. Остаточно маємо:
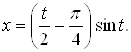
Знайдемо функцію Гріна для цієї крайової задачі
За функцію ![]() візьмемо
візьмемо 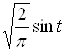 (коефіцієнт
(коефіцієнт ![]() вибирається з умови нормованості
вибирається з умови нормованості ![]() ) Розв'язком однорідного рівняння, який не задовольняє крайові умови, є, наприклад
) Розв'язком однорідного рівняння, який не задовольняє крайові умови, є, наприклад ![]() .
.
Далі рівняння
![]()
Має частинний розв'язок вигляду ![]() , отже, узагальнену функцію Гріна шукаємо у вигляді
, отже, узагальнену функцію Гріна шукаємо у вигляді
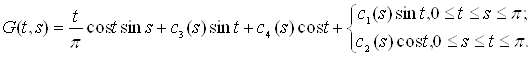
(коефіцієнт ![]() вбирають у себе функції
вбирають у себе функції ![]() і
і ![]() ).
).
Оскільки в нашому випадку ![]() , то умови неперервності і стрибка похідної функції
, то умови неперервності і стрибка похідної функції ![]() при
при ![]() мають вигляд
мають вигляд
![]() ,
,![]() .
.
Звідси ![]() ,
,![]() ;
;
Наслідком крайової умови в точці ![]() є рівність
є рівність ![]() . Тоді в точці
. Тоді в точці ![]() маємо:
маємо: ![]() .Отже, функція
.Отже, функція
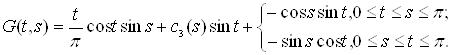
задовольняє пунктам 1-3 означення узагальненої функції Гріна.
Нарешті, функцію ![]() визначимо з умови ортогональності
визначимо з умови ортогональності
![]() . Обчисливши відповідні інтеграли, знаходимо
. Обчисливши відповідні інтеграли, знаходимо
![]()
![]()
Остаточно маємо
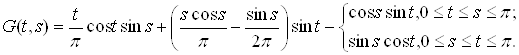
Похожие работы
... їнська мова повноцінно функціонує і розвивається, бо живлять її цілющі і життєдайні слова, які забезпечують вічне існування мові. 2. ОСОБЛИВОСТІ ФУНКЦІОНУВАННЯ ІМЕННИКІВ МНОЖИННОСТІ В УКРАЇНСЬКІЙ МОВІ 2.1 Множинні іменники Множинні іменники відмінюються лише у множині (а звідси і назва їх), однак значення однини вони мають: Темні окуляри приховували блиск очей (значення однини); На ві ...
... $G(t,T,x)$ називатимемо фундаментальнимрозв'язком двоточкової задачi (ФРДЗ) для рiвняння (4). У підрозділі 4.2 досліджується коректна розв'язність двоточкової задачі для еволюційних рівнянь з псевдо-Бесселевими операторами у просторах узагальнених функцій $Phi'$. Основний результат цього підрозділу складає наступне твердження. Теорема 4.1. Задача (4), (5) коректно розв'язна в класi узагальнених ...
... охорони державної таємниці в органах державної податкової служби Розділ 3. Структурні підрозділи ДПАУ, їх правовий статус, завдання та функції До складу Державної податкової адміністрації України входять слідуючи підрозділи: 1. Керівництво ДПАУ · Голова ДПАУ · Перший заступник Голови ДПАУ · Перший ...
... , але недостатньо стійке (можливі компроміси), якщо "в" — ставлення пасивне та недостатньо стійке, "г" — ставлення негативне, нестійке. 2.2. Психолого-педагогічна характеристика вихованця Результатом проведення різних методик щодо вивчення особистості учня стала психолого-діагностична карта-характеристика Марининої Тетяни. Психологічна характеристика учениці 9-В класу ЗОШ №9 М.ї Тетяни ...
0 комментариев