Навигация
Вычисляем k «теоретических» моментов
1. Вычисляем k «теоретических» моментов
![]() .
.
2. По выборке ![]() строим k одноименных выборочных моментов. В излагаемом контексте это будут моменты
строим k одноименных выборочных моментов. В излагаемом контексте это будут моменты
![]()
3. Приравнивая «теоретические» и одноименные им выборочные моменты, приходим к системе уравнений относительно компонент оцениваемого параметра
![]() (25.1)
(25.1)
4. Решая полученную систему (точно или приближенно), находим исходные оценки ![]() . Они, конечно, являются функциями от выборочных значений
. Они, конечно, являются функциями от выборочных значений ![]() .
.
Мы изложили порядок действий, исходя из начальных - теоретических и выборочных - моментов. Он сохраняется при ином выборе моментов, начальных, центральных или абсолютных, который определяется удобством решения системы (25.1) или ей подобной.
Перейдем к рассмотрению примеров.
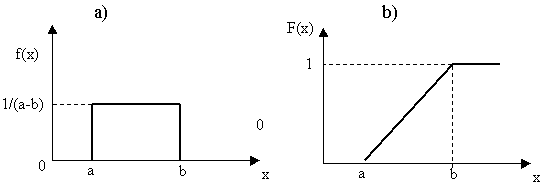
Пример 25.1. Пусть случайная величина x распределена равномерно на отрезке [ a ;b ] , где ![]() - неизвестные параметры. По выборке (
- неизвестные параметры. По выборке (![]() ) объема n из распределения случайной величины x. Требуется оценить a и b .
) объема n из распределения случайной величины x. Требуется оценить a и b .
Решение.
В данном случае распределение определяется плотностью
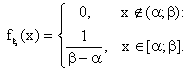
1) Вычислим первые два начальных «теоретических» момента:

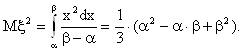
2) Вычислим по выборке два первых начальных выборочных момента

3) Составим систему уравнений
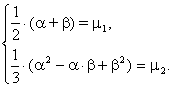
4) Из первого уравнения выразим a через b
![]()
и подставим во второе уравнение, в результате чего придём к квадратному уравнению
![]()
решая которое, находим два корня
![]() .
.
Соответствующие значения a таковы
![]() .
.
Поскольку по смыслу задачи должно выполнятся условие a < b , выбираем в качестве решения системы и оценок неизвестных параметров
![]() .
.
Замечая, что ![]() есть не что иное, как выборочная дисперсия
есть не что иное, как выборочная дисперсия ![]() , получаем окончательно
, получаем окончательно
![]() .
.
Если бы мы выбрали в качестве «теоретических» моментов математическое ожидание и дисперсию, ![]() , то пришли бы к системе (с учетом неравенства a < b)
, то пришли бы к системе (с учетом неравенства a < b)
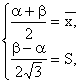
которая линейна и решается проще предыдущей. Ответ, конечно, совпадает с уже полученным.
Наконец, отметим, что наши системы всегда имеет решение и при том единственное. Полученные оценки, конечно, состоятельны, однако свойствам несмещенности не обладают.
7. Метод максимального правдоподобияИзучается, как и прежде, случайная величина x, распределение которой задается либо вероятностями её значений ![]() , если x дискретна, либо плотностью распределения
, если x дискретна, либо плотностью распределения ![]() , если x непрерывна, где
, если x непрерывна, где ![]() - неизвестный векторный параметр. Пусть (
- неизвестный векторный параметр. Пусть (![]() ) - выборка значений x. Естественно в качестве оценки
) - выборка значений x. Естественно в качестве оценки ![]() взять то значение параметра, при котором вероятность получения уже имеющейся выборки максимальна.
взять то значение параметра, при котором вероятность получения уже имеющейся выборки максимальна.
Выражение
![]()
называют функцией правдоподобия, она представляет собой совместное распределение или совместную плотность случайного вектора с n независимыми координатами, каждая из которых имеет то же распределение (плотность), что и x.
В качестве оценки неизвестного параметра ![]() берется такое его значение
берется такое его значение ![]() , которое доставляет максимум функции
, которое доставляет максимум функции ![]() , рассматриваемой как функции от
, рассматриваемой как функции от ![]() при фиксированных значениях
при фиксированных значениях ![]() . Оценку
. Оценку ![]() называют оценкой максимального правдоподобия. Заметим, что
называют оценкой максимального правдоподобия. Заметим, что ![]() зависит от объема выборки n и выборочных значений
зависит от объема выборки n и выборочных значений ![]()
![]() ,
,
и, следовательно, сама является случайной величиной.
Отыскание точки максимума функции ![]() представляет собой отдельную задачу, которая облегчается, если функция дифференцируема по параметру
представляет собой отдельную задачу, которая облегчается, если функция дифференцируема по параметру ![]() .
.
В этом случае удобно вместо функции ![]() рассматривать её логарифм, поскольку точки экстремума функции и её логарифма совпадают.
рассматривать её логарифм, поскольку точки экстремума функции и её логарифма совпадают.
Методы дифференциального исчисления позволяют найти точки, подозрительные на экстремум, а затем выяснить, в какой из них достигается максимум.
С этой целью рассматриваем вначале систему уравнений
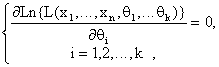 (25.2)
(25.2)
решения которой ![]() - точки, подозрительные на экстремум. Затем по известной методике, вычисляя значения вторых производных
- точки, подозрительные на экстремум. Затем по известной методике, вычисляя значения вторых производных
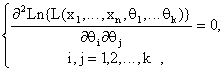
по знаку определителя, составленного из этих значений, находим точку максимума.
Оценки, полученные по методу максимального правдоподобия, состоятельны, хотя могут оказаться смещенными.
Рассмотрим примеры.
Пример 25.2. Пусть производится некоторый случайный эксперимент, исходом которого может быть некоторое события А, вероятность Р(А) которого неизвестна и подлежит оцениванию.
Решение.
Введем случайную величину x равенством
|
|
если событие А произошло,
если событие А не произошло (произошло событие ![]() ).
).
Распределение случайной величины x задается равенством
![]()
Выборкой в данном случае будет конечная последовательность (![]() ), где каждое из
), где каждое из ![]() может быть равно 0 либо 1.
может быть равно 0 либо 1.
Функция правдоподобия будет иметь вид
![]()
Найдем точку её максимума по р, для чего вычислим производную логарифма
![]()
Обозначим ![]() - это число равно количеству единиц «успехов» в выбранной последовательности.
- это число равно количеству единиц «успехов» в выбранной последовательности.
Приравняем полученную производную к нулю
![]()
и решим полученное уравнение
![]() .
.
Поскольку производная ![]() меняет знак с «+» на «-» при возрастании р от 0 до 1, точка
меняет знак с «+» на «-» при возрастании р от 0 до 1, точка ![]() есть точка максимума функции L, а
есть точка максимума функции L, а ![]() - оценка максимального правдоподобия параметра р. Заметим, что отношение
- оценка максимального правдоподобия параметра р. Заметим, что отношение ![]() есть частота появления события А в первых n испытаниях.
есть частота появления события А в первых n испытаниях.
Поскольку m есть число «успехов» в последовательности n независимых испытаний ( в схеме Бернулли), то ![]() , и
, и ![]() - несмещенная оценка. В силу закона больших чисел Бернулли
- несмещенная оценка. В силу закона больших чисел Бернулли ![]() стремится по вероятности к р, и оценка состоятельна.
стремится по вероятности к р, и оценка состоятельна.
Пример 25.3. Построим оценки неизвестных математического ожидания и дисперсии нормально распределенной случайной величины x с параметрами ![]() .
.
Р е ш е н и е.
В условиях примера случайная величина определяется плотностью распределения
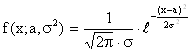 .
.
Сразу выпишем логарифм функции правдоподобия
 .
.
Составим систему уравнений для нахождения экстремальных точек

Из первого уравнения находим ![]() , из второго, подставляя найденное значение a, находим
, из второго, подставляя найденное значение a, находим ![]() .
.
Вычислим вторые производные функции lnL в точке (![]() ):
):
А = ![]() ,В =
,В = ![]() ,С =
,С = ![]() .
.
Поскольку определитель
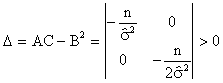 ,
,
а А < 0, то найденная точка в самом деле точка максимума функции правдоподобия.
Заметим, что оценка ![]() есть выборочное среднее (несмещенная и состоятельная оценка математического ожидания), а
есть выборочное среднее (несмещенная и состоятельная оценка математического ожидания), а ![]() - выборочная дисперсия (смещенная оценка дисперсии).
- выборочная дисперсия (смещенная оценка дисперсии).
Похожие работы
... на ЭВМ, колеблется в достаточно широких пределах в зависимости от класса объекта моделирования, вида оцениваемых характеристик, необходимой точности и достоверности результатов моделирования. Для метода статистического моделирования на ЭВМ характерно, что большое число операций, а соответственно большая доля машинного времени расходуются на действия со случайными числами. Кроме того, результаты ...
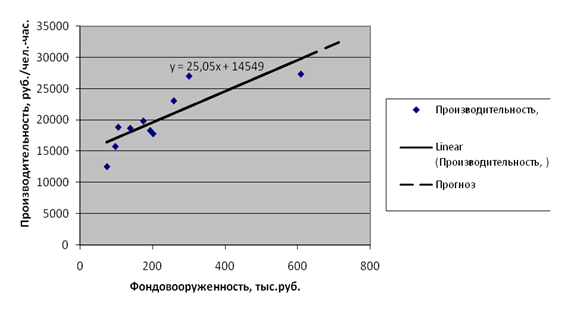
... тренд и производительность составит 30330,56 руб./ чел.-час. при коэффициенте фондовооруженности равного 630. Выводы и предложения Итак, проведенные исследования по проблемам повышения производительности труда в ООО «Меркит» позволяют сделать выводы и предложения, подтверждающие их научную новизну, теоретическую и практическую значимость. 1. Любому производству присуща в некотором ...
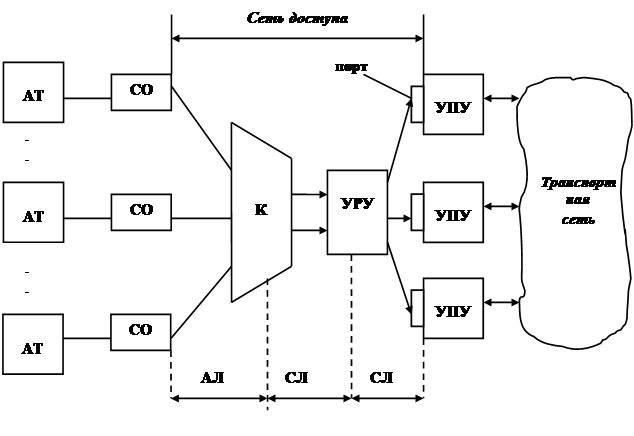
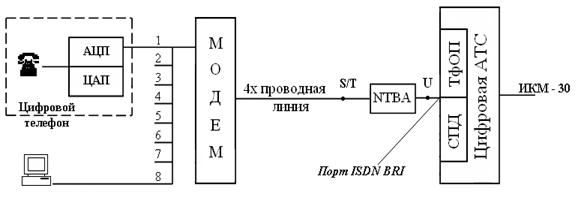
... своевременное распределение средств на развитие. Данными вопросами я и занимаюсь в настоящей дипломной работе. 4. Математическое моделирование Интернет - услуг 4.1 Математическое моделирование dial-up подключений Сначала рассмотрим моделирование услуги предоставления доступа в Интернет по dial-up, так как данная услуга является показателем потенциальных абонентов для монопольной услуги ...
... , которые поддаются математической формализации, моделируя, таким образом, отдельные элементы общего производственного процесса. Конечной целью моделирования производственно-экономической системы является подготовка и принятие руководителем предприятия управленческого решения. Модели производственно-экономических систем можно различать по следующим признакам: – по целям моделирования; – по ...
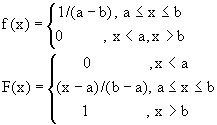
0 комментариев