Определенность

1.3  Определенность

Решение принимается в условиях определенности, когда руководитель может с точностью определить результат каждого альтернативного решения, возможного в данной ситуации. Сравнительно мало организационных или персональных решений принимается в условиях определенности. Однако они все-таки имеют место. Кроме того, элементы сложных крупных решений можно рассматривать как определенные. Уровень определенности при принятии решений зависит от внешней среды. Он увеличивается при наличии твердой правовой базы, ограничивающей количество альтернатив и снижающей уровень риска.

Как уже говорилось выше, решений, принимаемых в условиях абсолютной определенности, в реальной жизни быть не может. Однако существуют ситуации, когда решение принимается в условиях почти полной определенности. Например, решение о вложении нераспределенной прибыли в ценные бумаги государства. В данном случае менеджер точно знает размер вкладываемой суммы, может выбрать сроки вложения, рассчитать доходность и может точно подсчитать планируемую прибыль от данного вложения и сроки ее получения. Государство может не выполнить свои обязательства только при возникновении чрезвычайных обстоятельств, вероятность возникновения которых очень мала. (Ист. №6)

 

1.4  Методы

Решение может быть формальным и творческим. Принято считать, что если преобразование информации выполняется с помощью математических моделей, то выработанное решение считается формальным, если решение появляется в результате скрытой работы интеллекта человека, принимающего решение, то оно - творческое.

Такое деление в достаточной степени условно, поскольку чисто формального или чисто творческого решения не существует. Если решение вырабатывается с помощью математической модели, то знания и опыт человека (элементы творчества) используются при её создании, а интуиция (тоже момент творчества) – в момент, когда он задаёт то или иное значение параметра исходной информации или выбирает из множества альтернативных вариантов, полученных с помощью математической модели, один в качестве решения на управление. Если основным инструментом выработки решения является интеллект человека, то формальные методы, носителем которых практически является вся наука, скрыто присутствуют в его знаниях и опыте.

Формализуемые решения принимаются на основе соответствующих математических методов (алгоритмов). Математическая модель задачи оптимизации формализуемого решения включает следующие элементы:

1.  заданную оптимизируемую целевую функцию (критерий управляемости): Ф=F(x₁,x₂,:,x_n), где x_j (j=1,2,:,n) - параметры, учитываемые при принятии решения (отражающие ресурсы принятия решений);

2.  условия, отражающие ограниченность ресурсов и действий ЛПР при принятии решений: g_i(x_j)<a_i, k_i (x_j)=b_i; c_j<x_j<d_i, i=1,2,:,m; j=1,2,:, n.

Непременным требованием для решения задачи оптимизации является условие n>m.

В зависимости от критерия эффективности, стратегий и факторов управления выбирается тот или иной метод (алгоритм) оптимизации.

Основными являются следующие классы методов:

1.  методы линейного и динамического программирования (принятия решения об оптимальном распределении ресурсов);

2.  методы теории массового обслуживания (принятие решения в системе со случайным характером поступления и обслуживания заявок на ресурсы);

3.  методы имитационного моделирования (принятие решения путем проигрывания различных ситуаций, анализа откликов системы на различные наборы задаваемых ресурсов);

4.  методы теории игр (принятие решений с помощью определения стратегии в тех или иных состязательных задачах);

5.  методы теории расписаний (принятие решений с помощью разработки календарных расписаний выполнения работ и использования ресурсов);

6.  методы сетевого планирования и управления (принятие решений с помощью оценки и перераспределения ресурсов при выполнении проектов, изображаемых сетевыми графиками);

7.  методы многокритериальной (векторной) оптимизации (принятие решений при условии существования многих критериев оптимальности решения)

и другие методы. (Ист. №9)

 

2. Некорректно поставленные задачи

В качестве основного объекта рассматривается операторное уравнение: Az = u , где A - линейный оператор, действующий из гильбертова пространства Z в гильбертово пространство U. Требуется найти решение операторного уравнения z, соответствующее заданной неоднородности (или правой части уравнения) u.

Такое уравнение является типичной математической моделью для многих физических, так называемых обратных, задач, если предполагать, что искомые физические характеристики z не могут быть непосредственно измерены, а в результате эксперимента могут быть получены только данные u, связанные с z с помощью оператора A.

Французским математиком Ж. Адамаром были сформулированы следующие условия корректности постановки математических задач, которые мы рассмотрим на примере записанного операторного уравнения. Задача решения операторного уравнения называется корректно поставленной (по Адамару), если выполнены следующие три условия (условия корректности):

1) задача имеет решение при любых допустимых исходных данных (решение существует ∀u ∈U);

2) каждым исходным данным u соответствует только одно решение (решение единственно);

3) решение устойчиво (если u n →u ,  , Az = u , то z n →z).

Смысл первого условия заключается в том, что среди исходных данных нет противоречащих друг другу условий, что исключало бы возможность решения задачи.

Второе условие означает, что исходных данных достаточно для однозначной определённости решения задачи. Эти два условия обычно называют условиями математической определённости задачи. Условие 2) обеспечивается тогда и только тогда, когда оператор A является взаимно однозначным (инъективным). Условия 1) и 2) означают, что существует обратный оператор  , причем его область определения D() (или множество значений оператора A, R(A)) совпадает с U.

Условие 3) означает, что обратный оператор  является непрерывным, т.е. “малым” изменениям правой части u соответствуют “малые” изменения решения z. Третье условие обычно трактуется как физическая детерминированность задачи. Это объясняется тем, что исходные данные физической задачи, как правило, задаются с некоторой погрешностью; при нарушении же третьего условия как угодно малые возмущения исходных данных могут вызывать большие отклонения в решении.

Задачи, не удовлетворяющие хотя бы одному условию корректности, называются некорректными задачами (или некорректно поставленными). Более того, Ж. Адамар считал, что только корректные задачи должны рассматриваться при решении практических задач. Однако хорошо известны примеры некорректно поставленных задач, к изучению и численному решению которых приходится прибегать при рассмотрении многочисленных прикладных задач. Нужно отметить, что устойчивость и неустойчивость решения связаны с тем, как определяется пространство решений Z. Выбор пространства решений (в том числе и нормы в нем) обычно определяется требованиями прикладной задачи. Задачи могут быть некорректно поставленными при одном выборе нормы и корректно поставленными при другом.

Многочисленные обратные (в том числе и некорректные) задачи можно найти в различных областях физики. Так, астрофизик не может активно воздействовать на процессы, происходящие на далеких звездах и галактиках, ему приходится делать заключения о физических характеристиках весьма удаленных объектов по их косвенным проявлениям, доступным измерениям на Земле или вблизи Земли (на космических станциях). Прекрасные примеры некорректных задач можно найти в медицине, прежде всего, нужно отметить вычислительную (или компьютерную) томографию. Хорошо известны приложения некорректных задач в геофизике (на самом деле, легче и дешевле судить о том, что делается под поверхностью Земли, решая обратные задачи, чем заниматься бурением глубоких скважин), радиоастрономии, спектроскопии, ядерной физике и т.д., и т.п.

Хорошо известным примером некорректно поставленной задачи является интегральное уравнение Фредгольма 1-го рода. Пусть оператор A имеет вид:

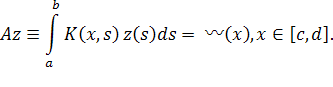
Пусть ядро интегрального оператора K(x, s) - функция, непрерывная по совокупности аргументов x ∈[c, d], s ∈[a,b], а решение z(s) - непрерывная на отрезке [a,b] функция. Тем самым, можно рассматривать оператор A как действующий в следующих пространствах: A :C[a,b]→ C[c, d]. (Пространство C[a,b] состоит из функций, непрерывных на отрезке [a,b]. Норма z ∈C[a,b]определяется как ). Покажем, что в этом случае задача решения интегрального уравнения является некорректно поставленной. Для этого нужно проверить условия корректности постановки задачи:

1)  Существование решения для любой непрерывной на [c, d] функцииu(x) . На самом же деле, это не так: существует бесконечно много непрерывных функций, для которых решения нет.

2) Единственность решения. Это условие выполняется в том и только в том случае, если ядро интегрального оператора замкнуто.

Первые два условия корректности эквивалентны условию существования обратного оператора  с областью определения D()=C[c,d]. Если ядро интегрального оператора замкнуто, то обратный оператор существует, однако область его определения не совпадает с C[c,d].

3)  Устойчивость решения. Это означает, что для любой последовательности  последовательность z n →. Устойчивость эквивалентна непрерывности обратного оператора  при условии, что обратный оператор существует. В данном случае это не так, что видно из следующего примера. Пусть последовательность непрерывных функций  , n=1, 2, …, такая, что  на промежутке  и обращается в нуль вне данного интервала, max| z (s) |=1, s∈[a, b], а последовательность чисел d → 0 +0 .

4)  Такая функция может быть выбрана, например, кусочно-линейной. Тогда для любого x ∈[c, d]

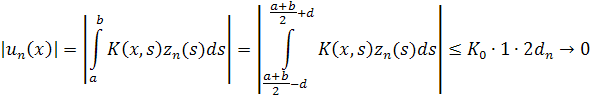
при

Последовательность функций  равномерно, т.е. по норме C[c,d], сходится к  = 0.

Хотя решение уравнения  в этом случае  = 0 , последовательность  не стремится к  , так как.

Интегральный оператор A является вполне непрерывным при действии из  в

, при действии из C[a,b] в  и при действии из C[a,b] в C[c,d]. (Пространство

 состоит из функций, интегрируемых с квадратом на отрезке [a,b]. Норма z∈ определяется как  ). Это означает, что любую ограниченную последовательность этот оператор преобразует в компактную. Компактная последовательность по определению обладает тем свойством, что из любой ее подпоследовательности можно выделить сходящуюся. Легко указать последовательность  , , из которой нельзя выделить сходящуюся в C[a,b] подпоследовательность. Например,

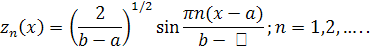
Нормы всех членов этой последовательности равны 1 в  , но из любой подпоследовательности этой последовательности нельзя выделить сходящуюся, поскольку  . Очевидно, что эта последовательность состоит из непрерывных на [a,b] функций и равномерно (по норме C[a,b]) ограничена, но из этой последовательности нельзя выделить сходящуюся в C[a,b] подпоследовательность (тогда она сходилась бы и в , поскольку из равномерной сходимости следует сходимость в среднем). Если предположить, что оператор  является непрерывным, то легко прийти к противоречию. Для существования обратного оператора достаточно потребовать, чтобы прямой оператор A был инъективным. Очевидно, что, если оператор B: C[c,d]→C[a,b] непрерывный, а оператор A вполне непрерывный, то BA :C[a,b] →C[a,b] - тоже вполне непрерывный оператор. Но тогда, поскольку для любого n , то последовательность  компактна, что неверно. Оператор, обратный к вполне непрерывному оператору, не может быть непрерывным. Аналогичное доказательство может быть проведено для любых бесконечномерных банаховых (т.е. полных нормированных) пространств.

Поскольку задача решения интегрального уравнения Фредгольма первого рода в указанных пространствах некорректно поставлена, то даже при очень малых ошибках в задании u(x) решение может либо отсутствовать, либо как угодно сильно отличаться от искомого точного решения.

Итак, вполне непрерывный инъективный оператор обладает обратным оператором, который не является непрерывным (ограниченным). Более того, при действии в бесконечномерных банаховых пространствах множество значений вполне непрерывного оператора не является замкнутым. Поэтому как угодно близко к неоднородности u(x) , для которой решение операторного уравнения существует, найдется неоднородность, для которой решение отсутствует.

Некорректность постановки математической задачи может быть связана с ошибкой в задании оператора. Простейший пример дает задача отыскания нормального псевдорешения системы линейных алгебраических уравнений и возникающая при этом неустойчивость, связанная с ошибками задания матрицы.

Пусть дана система линейных алгебраических уравнений (СЛАУ):

Система может и не иметь решений. Гаусс и Лежандр в начале XIX века ввели метод наименьших квадратов, а именно, вместо решения СЛАУ предложили минимизировать квадратичный функционал (невязку):

 - сопряженная (транспонированная) матрица. Поскольку матрица  неотрицательно

определена, то Ф(x)- выпуклый функционал. Для выпуклого функционала задача отыскания  эквивалентна отысканию стационарной точки, т.е. решения уравнения Ф'(x) = 0 . Легко видеть, что Ф' (x) = 2 ⋅ (Ax −b), Ф''(x) = 2 ⋅A ≥0.

Из равенства градиента нулю получается система линейных алгебраических уравнений с квадратной неотрицательно определенной матрицей (система нормальных уравнений):

В конечномерном случае легко доказать, что для любого вектора b система нормальных

уравнений всегда имеет решение (для исходного же уравнения это не обязательно), которое называется псевдорешением системы Ax = b . Псевдорешение может быть неединственным (если определитель det(A) =0; если же det(A) ≠0, то псевдорешение единственно). Множество псевдорешений образует аффинное (или линейное) подпространство и является выпуклым и замкнутым.

Если же система Ax =b имеет решение, то оно совпадает с решением системы  Ax = b . В этом случае minФ(x) =μ=0. Если же minФ(x) =μ>0, система Ax = b не имеет решений, но, как уже указывалось выше, имеет псевдорешение (возможно, неединственное). Число μ обычно называется мерой несовместности системы Ax = b .

Определение. Нормальное псевдорешение  системы Ax = b – это псевдорешение с

минимальной нормой, что является решением задачи отыскания минимума .

Можно привести много др. примеров классических математических задач, являющихся некорректными при совершенно естественном выборе понятий меры точности как для исходных данных задачи, так и для возможных решений: решение систем линейных алгебраических уравнений с определителем, равным нулю; задача оптимального планирования; решение интегральных уравнений 1-го рода; задача аналитического продолжения; суммирование рядов Фурье; большое число краевых задач для уравнении с частными производными. (Ист. №10)

 

3.  Регуляризирующие алгоритмы

Пусть дано операторное уравнение: Az = u , где A - линейный оператор, действующий из нормированного пространства Z в нормированное пространство U. В 1963 г. А.Н.Тихонов дал знаменитое определение регуляризирующего алгоритма (РА), которое лежит в основе современной теории некорректно поставленных задач.

Определение. Регуляризирующим алгоритмом (регуляризирующим оператором)  называется оператор, обладающий двумя следующими свойствами:

1)  определен для любых δ > 0 ,  ∈U , и отображает (0,+ ∝) ×U в Z;

2) для любого z ∈ Z и для любого  ∈U такого, что Az = u ,

.

Задача решения уравнения первого рода называется регуляризируемой, если существует хотя бы один регуляризирующий алгоритм. Непосредственно из определения следует, что если существует хотя бы один РА, то их существует бесконечно много.

В настоящее время все математические задачи можно разделить на следующие классы:

1) корректно поставленные задачи;

2) некорректно поставленные регуляризируемые задачи;

3) некорректно поставленные нерегуляризируемые задачи.

Понятно, что корректно поставленные задачи являются регуляризируемыми, поскольку можноположить  . Отметим, что знание δ > 0 в этом случае необязательно.

Далеко не все некорректно поставленные задачи можно регуляризировать, причем это часто зависит от выбора пространств Z, U. Российский математик Л.Д.Менихес построил пример интегрального оператора с непрерывным замкнутым ядром, действующего из пространства C[0,1] в , обратная задача для которого (т.е. решение интегрального уравнения Фредгольма 1-го рода) является нерегуляризируемой. Это связано со свойствами пространства C[0,1]. Ниже будет показано, что если пространство Z гильбертово, а оператор A ограниченный и инъективный, то задача решения операторного уравнения первого рода является регуляризируемой. Этот результат справедлив и для некоторых банаховых пространств, но не для всех. В частности, пространство C[0,1] к таким банаховым пространствам не относится.

Можно дать эквивалентное определение регуляризирующего алгоритма и регуляризируемости операторного уравнения. Пусть задан оператор (отображение) , причем  определен для любых δ > 0,  ∈U , и отображает (0,+ ∝) ×U в Z. Погрешность решения операторного уравнения в точке z ∈ Z с помощью оператора  при условии, что правая часть u задана с погрешностью δ >0, определяется как

Оператор  называется регуляризирующим оператором, если для любого z ∈ Z  . Легко видеть, что данное определение эквивалентно данному выше.

Аналогично можно дать определение регуляризирующего алгоритма для задачи вычисления значений оператора (см. конец предыдущего параграфа), т.е. для задачи вычисления значений отображения G : D(G) → Y, D(G) ⊆ X при условии, что аргумент задан с погрешностью (X, Y – метрические или нормированные пространства). Разумеется, задача решения операторного уравнения при условии, что A – инъективный оператор, может рассматриваться как задача вычисления значений оператора .

Огромное значение имеет ответ на следующий очень важный вопрос, можно ли решить некорректную задачу, т.е. построить регуляризирующий алгоритм, не зная погрешность δ Если задача корректна, то устойчивый метод, очевидно, можно построить и без знания δ.

Так, в случае решения операторного уравнения . В случае некорректных задач это невозможно. Приведенная ниже теорема принадлежит А.Б.Бакушинскому и была им доказана для задачи вычисления значений оператора. Аналогичная теорема имеет место и для решения операторного уравнения.

Теорема. Если для вычислений значений оператора G на множестве D(G) ⊆ X существует регуляризирующий оператор, не зависящий от δ (явно), то существует продолжение G на X , которое непрерывно на D(G) ⊆ X.

Итак, построение регуляризирующих алгоритмов, не зависящих явно от погрешности,

возможно только для задач, корректных на своей области определения.

Следующим свойством некорректно поставленных задач является невозможность оценить погрешность решения, даже если известна погрешность задания правой части операторного уравнения или погрешность задания аргумента в задаче вычисления значений оператора. Этот принципиально важный результат был также впервые доказан А.Б.Бакушинским для решения операторного уравнения.

Теорема. Пусть 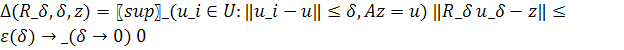 для любого z ∈ D ⊆ Z . Тогда сужение обратного оператора на множество AD: непрерывно на AD. Таким образом, равномерная по z оценка погрешности решения операторного уравнения на множестве D ⊆ Z возможна только в том случае, когда обратный оператор непрерывен на AD. Таким образом, равномерная по z оценка погрешности решения операторного уравнения на множестве D ⊆ Z возможна только в том случае, когда обратный оператор непрерывен на AD. Данная теорема справедлива и для нелинейных операторных уравнений, причем в метрических пространствах.

Из определения регуляризирующего алгоритма легко следует, что, если есть хотя бы один регуляризирующий алгоритм, то их может быть сколько угодно. Выбрать же тот, который дает наименьшую ошибку, или сравнивать алгоритмы, сравнивая ошибки полученных приближенных решений, при решении некорректных задач, невозможно при отсутствии априорной информации, которая фактически преобразует такие задачи в корректные.

Регуляризирующие алгоритмы для операторных уравнений в бесконечномерных банаховых пространствах нельзя сравнивать и по скорости сходимости приближенного решения к точному при стремлении погрешности входных данных к нулю. Этот важный результат принадлежит В.А.Винокурову. (Ист. №1)

4.  Адаптивные регуляризирующие алгоритмы