Навигация
ЭЙЛЕРОВЫ ГРАФЫ
Выполнила студентка 4 курса
42 группы математического
факультета Катышева Н.Г.
Научный руководитель:
Токаревская С.А.
Архангельск
2004
Оглавление
Введение............................................................................................. 3
Глава 1. Теоретическая часть............................................................ 4
Основные понятия теории графов..................................................... 4
Маршруты и связность...................................................................... 6
Задача о кёнигсбергских мостах.................................................... 7
Эйлеровы графы............................................................................... 9
Оценка числа эйлеровых графов.................................................... 13
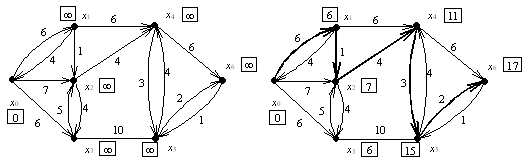
Алгоритм построения эйлеровой цепи в данном эйлеровом графе. 14
Глава 2. Практическая часть........................................................... 15
Заключение....................................................................................... 24
Литература....................................................................................... 25
Введение
Первая работа по теории графов, принадлежащая известному швейцарскому математику Л.Эйлеру, появилась в 1736г. Вначале теория графов казалась довольно незначительным разделом математики, так как она имела дело в основном с математическими развлечениями и головоломками. Однако дальнейшее развитие математики и особенно её приложений дало сильный толчок развитию теории графов. Уже в XIX столетии графы использовались при построении схем.
В настоящее время эта теория находит многочисленное применение в разнообразных практических вопросах: при установлении разного рода соответствий, при решении транспортных задач, задач о потоках в сети нефтепроводов, в программировании и теории игр, теории передачи сообщений. Теория графов теперь применяется и в таких областях, как экономика, психология и биология.
В этой работе мы подробнее рассмотрим эйлеровы графы, основные сведения и теоремы, связанные с этим понятием. А также задачи, которые решаются с помощью эйлеровых графов.
Глава 1. Теоретическая часть. Основные понятия теории графов
Граф G – пара (V,X), где V конечное непустое множество, содержащее p вершин, а множество Х содержит q неупорядоченных пар различных вершин из V.
Каждую пару X={u,v} вершин в Х называют ребром графа G и говорят, что Х соединяет u и v.Мы будем писать X=uv и говорить, что u и v – смежные вершины. Вершина u и ребро Х инцидентны, так же как v и Х. Если два различных ребра X и Y инцидентны одной и той же вершине, то они называются смежными. Граф с р вершинами и q ребрами называется (p;q)- графом. Граф (1,0)- называется тривиальным.[6]
Если элементом множества V может быть пара одинаковых элементов u, то такой элемент множества V называется петлёй.[3]
Типы графов:
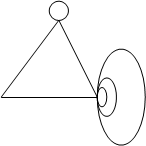
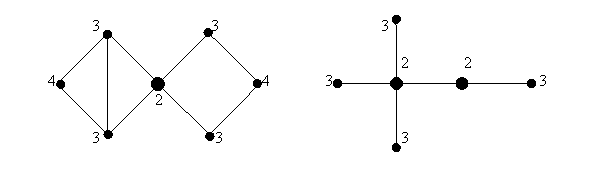
· Мультиграф, в нём не допускаются петли, но пары вершин могут соединяться более чем одним ребром, эти рёбра называются кратными (рис.1).
· Псевдограф, в нём допускаются петли и кратные рёбра (рис.2).
 | |||
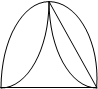 | |||
Рис.1 Рис.2
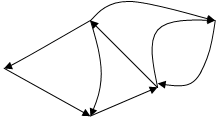
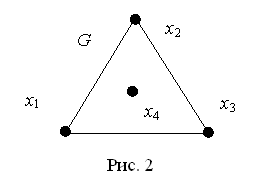
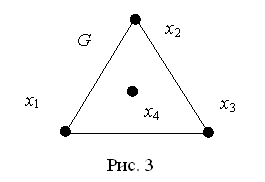
· Ориентированный граф, или орграф, состоит из конечного непустого множества V вершин и заданного набора Х упорядоченных пар различных вершин. Элементы из Х называются ориентированными рёбрами, или дугами. Нет петель и кратных дуг (рис. 3).
 | ||||||||
 | ||||||||
|
| |||||||
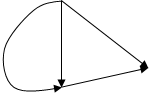
· Направленный граф – это орграф, не имеющий симметричных пар ориентированных рёбер (рис.4).
· Помеченные графы (или перенумерованные), если его вершины отличаются одна от другой какими-либо пометками. В качестве пометок обычно используются буквы или целые числа.[6]
Степенью вершины vi в графе G называется число рёбер, инцидентных vi ,обозначается di.[6] Для орграфа вводятся понятия степени входа и выхода. Степенью выхода вершины v называется количество рёбер, для которых v является начальной вершиной, обозначается outdeg(v). Степенью входа вершины v называется количество рёбер , для которых v является конечной вершиной, обозначается indeg(v). Если indeg(v)=0, то вершина v называется источником. Если outdeg(v)=0, то вершина v называется стоком.[1]
Маршруты и связность
Граф G/(U/,V/) называется подграфом графа G(U,V), если U/ÌU и V/ÌV. Обозначение: G/ÌG.
Если V/=V, то G/ называется остовным подграфом G.[3]
Маршрутом в графе G называется чередующаяся последовательность вершин и рёбер v0,x1,v1,…vn-1,xn,vn; эта последовательность начинается и кончается вершиной, и каждое ребро последовательности инцидентно двум вершинам, одна из которых непосредственно предшествует ему, а другая непосредственно следует за ним. Указанный маршрут соединяет вершины v0 и vn и его можно обозначить v0v1v2…vn (наличие рёбер подразумевается). Эта последовательность иногда называется (v0-vn)-маршрутом. Маршрут замкнут, если v0=vn, и открыт в противном случае. Маршрут называется цепью, если все его рёбра различны, и простой цепью, если все вершины (а следовательно, и рёбра ) различны. Замкнутая цепь называется циклом. Замкнутый маршрут называется простым циклом, если все его n вершин различны и n³3.
Граф G называется связным, если любая пара его вершин соединена простой цепью.[6]
Задача о кёнигсбергских мостах.
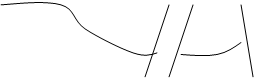
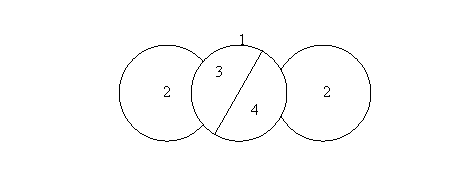
Отцом теории графов является Эйлер (1707-1782), решивший в 1736г. широко известную в то время задачу, называвшуюся проблемой Кёнигсбергских мостов. В городе Кёнигсберге (ныне Калининград) было два острова, соединенных семью мостами с берегами реки Преголя и друг с другом так, как показано на рисунке 5. Задача состояла в следующем: найти маршрут прохождения всех четырёх частей суши, который начинался бы с любой из них, кончался бы на этой же части и ровно один раз проходил по каждому мосту.
 | |||
 | |||
![]()
 |  | |||||||||||||||||
 | ||||||||||||||||||
 | ||||||||||||||||||
 | ||||||||||||||||||
Рис.5.
Легко, конечно попытаться решить эту задачу эмпирически, производя перебор всех маршрутов, но все попытки окончатся неудачей. Исключительный вклад Эйлера в решение этой задачи заключается в том, что он доказал невозможность такого маршрута.
Для доказательства того, что задача не имеет решения, Эйлер обозначил каждую часть суши точкой (вершиной), а каждый мост – линией (ребром), соединяющей соответствующие точки. Получился “граф”. Этот граф показан на рисунке 6, где точки отмечены теми же буквами, что и четыре части суши на рисунке 5.

Рис.6.
Утверждение о не существовании “положительного” решения у этой задачи эквивалентно утверждению о невозможности обойти специальным образом граф, представленный на рисунке 6.
Отправляясь от этого частного случая Эйлер обобщил постановку задачи и нашёл критерий существования обхода у данного графа, а именно граф должен быть связным и каждая его вершина должна быть инцидентна чётному числу рёбер.[6]
Эйлеровы графы
Решение Эйлером задачи о Кёнигсбергских мостах привела к первой опубликованной работе по теории графов. Задачу об обходе мостов можно обобщить и получить следующую задачу теории графов: можно ли найти в данном графе G цикл, содержащий все вершины и все рёбра? Граф, в котором это возможно, называется эйлеровым. Таким образом, эйлеров граф имеет эйлеров цикл – замкнутую цепь, содержащую все вершины и все рёбра. Ясно, что эйлеров граф должен быть связным.[6]
Если снять ограничения на замкнутость цепи, то граф называется полуэйлеровым.
Теорема 1(критерий):
Граф с более чем одной вершиной имеет эйлеров цикл тогда и только тогда, когда он связный и каждая его вершина имеет чётную степень.
Доказательство: Предположим, что граф G имеет эйлеров цикл. Граф является связным, так как каждая вершина принадлежит циклу. Для всякой вершины v графа G каждый раз, когда эйлеров цикл проходит через v, он вносит 2 в степень v. Поэтому степень v чётная.
Обратно, нужно показать, что каждый связный граф, у которого степени вершин чётные, имеет эйлеров цикл. Докажем эту теорему, используя индукцию по числу вершин. Поскольку теорема тривиально справедлива при n£3, начнём индукцию с n=3. Предположим, что каждый связный граф, имеющий менее k вершин, и все вершины которого обладают чётной степенью, содержит эйлеров цикл. Пусть G – связный граф, содержащий k вершин, степени которых чётные. Допустим, что v1 и v2 - вершины графа G. Поскольку граф G – связный, существует путь из v1 в v2 .Поскольку степень v2 – чётная, существует неиспользованное ребро, по которому можно продолжить путь. Поскольку граф конечный, то путь, в конце концов, должен вернуться в v1 , и эйлеров цикл С1 можно считать построенным. Если С1 является эйлеровым циклом для G, тогда доказательство закончено. Если нет, то пусть G/ - подграф графа G, полученный удалением всех рёбер, принадлежащих С1. Поскольку С1 содержит чётное число рёбер, инцидентных каждой вершине, каждая вершина подграфа G/ имеет чётную степень.
Пусть e – ребро графа G/ , пусть Ge – компонента графа G/ , содержащая е. Поскольку G/ имеет менее, чем k, вершин, и у каждой вершины графа G/ чётная степень, граф G/ имеет эйлеров цикл. Пусть С2 . Далее у С1 и С2 имеется общая вершина, допустим, а. Теперь можно продолжить эйлеров цикл, начиная его в а, пройти С1 , вернуться в а, затем пройти С2 и вернуться в а. Если новый эйлеров цикл не является эйлеровым циклом для G, продолжаем использовать этот процесс, расширяя наш эйлеров цикл, пока, к конце концов, не получим эйлеров цикл для G.[1]
Из теоремы 1 следует, что если в связном графе G нет вершин с нечётными степенями, то в G есть замкнутая цепь, содержащая все вершины и все рёбра графа G. Аналогичный результат справедлив для связных графов, имеющих некоторое число вершин с нечётными степенями.
Следствие 1(а): Пусть G- связный граф, в котором 2n вершин имеют нечётные степени, n>1. Тогда множество рёбер графа G можно разбить на n открытых цепей.
Следствие 1(б): Пусть G- связный граф, в котором две вершины имеют нечётные степени. Тогда в G есть открытая цепь, содержащая все вершины и все рёбра графа G (и начинающаяся в одной из вершин с нечётной степенью, а кончающаяся в другой).[6]
Эйлеровым путём в графе называется путь, содержащий все рёбра графа. Эйлеров путь называется собственным, если он не является эйлеровым циклом.[1]
Теорема 2: Если граф G обладает эйлеровым путём с концами А и В (А не совпадает с В), то граф G связный и А и В – единственные нечётные его вершины.
Доказательство: Связность графа следует из определения эйлерова пути. Если путь начинается в А, а заканчивается в другой вершине, то и А и В – нечётные даже если путь неоднократно проходил через А и В. В любую другую вершину графа путь должен был привести и вывести из неё, то есть все остальные вершины должны быть чётными.
Теорема 3: (обратная) Если граф G связный и А и В единственные нечётные вершины его, то граф G обладает эйлеровым путём с концами А и В.
Доказательство: Вершины А и В могут быть соединены ребром в графе, а могут быть соединены.
Если А и В соединены ребром, то удалим его; тогда все вершины станут чётными. Новый граф (по теореме 1) обладает эйлеровым циклом, началом и концом которого может служить любая вершина. Начнём эйлеров путь в вершине А и кончим его в вершине А. Добавим ребро (А,В) и получим эйлеров путь с началом в А и концом в В.
Если А и В не соединены ребром, то к графу добавим новое ребро (А,В), тогда все вершины его станут чётными. Новый граф (по теореме 1) обладает эйлеровым циклом. Начнём его из вершины А по ребру (А,В). Заканчивается путь тоже в вершине А. Если удалить теперь из полученного цикла ребро (А,В), то останется эйлеров путь с началом в В и концом в А или началом в А и концом В.
Таким образом, всякую замкнутую фигуру, имеющую в точности две нечётные вершины, можно начертить одним росчерком без повторений, начав в одной из нечётных вершин, а кончив в другой.
Теорема 4: Если связный граф G имеет 2k нечётных вершин, то найдётся семейство из k путей, которые в совокупности содержат все рёбра графа в точности по одному разу.
Доказательство: Половину нечётных вершин обозначим А1,А2,…,Аk,другую половину В1,В2,…,Вk(рис.7). Если вершины Аi и Вi (1<i<k) соединены ребром, то удалим из графа G ребро (Аi,Вi). Если вершины А и В не соединены ребром, то добавим к G ребро (Аi,Вi). Все вершины нового графа будут чётными, то есть в новом графе найдётся эйлеров цикл. При восстановлении графа G цикл разобьется на k отдельных путей, содержащих все рёбра графа.[2]
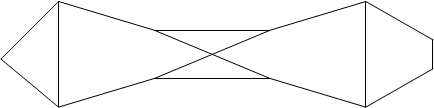
Рис.7
Пусть G=(V,E) – ориентированный граф. Ориентированным циклом называется ориентированный путь ненулевой длины из вершины в ту же вершину без повторения ребер.
Пусть G=(V,E) – ориентированный граф. Ориентированный цикл, который включает все рёбра и вершины графа G, называется эйлеровым циклом. Говорят, что ориентированный граф G имеет эйлеров цикл.
Теорема 5: Ориентированный граф имеет эйлеров цикл тогда и только тогда, когда он связный и степень входа каждой вершины равна степени выхода.[1]
Оценка числа эйлеровых графов
Лемма : В любом графе число вершин нечётной степени чётно.
Доказательство: По теореме 1 сумма степеней всех вершин число чётное. Сумма степеней вершин чётной степени чётна, значит, сумма степеней вершин нечётной степени также чётна, значит, их чётное число.
Пусть G(p) – множество всех графов с р вершинами, а Е(р) – множество эйлеровых графов с р вершинами.
Теорема 6: Эйлеровых графов почти нет, то есть
lim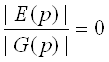
Доказательство: Пусть E/ (р) – множество графов с р вершинами и чётными степенями. Тогда по теореме1 Е(р)ÌЕ/(p) и |Е(р)|£|Е/(p)|.В любом графе число вершин нечётной степени чётно, следовательно, любой граф из Е/(p) можно получить из некоторого графа G(p-1), если добавить новую вершину и соединить её со всеми старыми вершинами нечётной степени. Следовательно, |Е/(p)| £|G(p-1)|. Но |G(p)|=2C(p, 2). Заметим, что
С(k,2)-C(k-1,2)=
= ![]()
Далее имеем:
|Е(р)|£|Е/(p)| £|G(p-1)| = 2C( p-1,2) =2C(p,2)-(p-1) = |G(p)|2-(p-1)
и
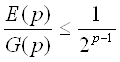 , откуда lim
, откуда lim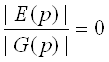 . [3]
. [3]
Этот метод известен под названием алгоритма Флёри.
Теорема 7: Пусть G – эйлеров граф, тогда следующая процедура всегда возможна и приводит к эйлеровой цепи графа G. Выходя из произвольной вершины и, идём по рёбрам графа произвольным образом, соблюдая лишь следующие правила:
1) стираем рёбра по мере их прохождения и стираем также изолированные вершины, которые при этом образуются;
2) на каждом этапе идём по мосту только тогда, когда нет других возможностей.
Доказательство: Покажем сначала, что указанная процедура может быть выполнена на каждом этапе. Предположим, что мы достигли некоторой вершины V; тогда если V¹U, то оставшийся подграф H связен и содержит ровно две вершины нечётной степени, а именно U и V. Согласно теореме 3 и определению полуэйлерова графа, граф H содержит полуэйлерову цепь P из V в U. Поскольку удаление первого ребра цепи Р не нарушает связности графа Н, то описанное в теореме построение (Т 1б)) возможно на каждом этапе. Если же V=U, то доказательство остаётся тем же самым до тех пор, пока есть ещё рёбра, инцидентные вершине U.
Осталось только показать, что данная процедура всегда приводит к полной эйлеровой цепи. Но это очевидно, так как в G не может быть рёбер, оставшихся не пройденными после использования последнего ребра, инцидентного U. В противном случае удаление некоторого ребра, смежного одному из оставшихся, привело бы к несвязному графу, что противоречит условию 2).[5]
Глава 2. Практическая часть
Задачи:
Похожие работы
... петля учитывается дважды. В случае ориентированного графа различают степень do(v) по выходящим дугам и di(v) — по входящим. §2. Условия существования гамильтонова цикла В отличии от эйлеровых графов, где имеется критерий для графа быть эйлеровым, для гамильтоновых графов такого критерия нет. Более того, задача проверки существования гамильтонова цикла оказывается NP-полной. Большинство известных ...
... G. Таким образом, доказана. Теорема 4. Пусть G — связный граф с k>0 вершинами нечетной степени. Тогда минимальное число непересекающихся по ребрам простых цепей, покрывающих G, равно k/2. Алгоритм построения эйлерова цикла Для начала отметим, что теорема 1 также дает метод построения эйлерова цикла. Здесь мы рассмотрим несколько иной алгоритм. Пусть G(X, E) — связный неорентированный ...
... структур данных для представления в программе объектов математической модели – это основа искусства практического программирования. Далее приводится четыре различных базовых представления графов. Выбор наилучшего представления определяется требованиями конкретной задачи. Более того, при решении конкретных задач используются, как правило, некоторые комбинации или модификации указанных ...
... в 2 или более раз. Заключение В данной работе мы познакомились с основными понятиями, определениями и результатами, связанными с гамильтоновыми графами и циклами. Так же мы рассмотрели ту часть теории сложности, которая затрагивает задачи отыскания гамильтонова цикла. И в итоги проведённых изучений была написана программа отыскания гамильтонова цикла в графе. Список литературы 1. ...
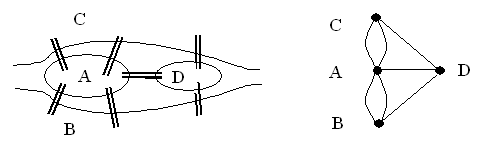
0 комментариев