Теорема Бернулли. Закон распределения Пуассона. Критерий Колмогорова

Московский Государственный Авиационный

Институт

(Технический Университет)

Филиал „Взлёт“

Курсовая работа

«Теорема Бернулли. Закон распределения Пуассона. Критерий Колмогорова»

Задание 1. Проверка выполнимости теоремы Бернулли на примере вероятности прохождения тока по цепи

Теорема утверждает, что при большом числе опытов частота события приближается (точнее - сходится по вероятности) к вероятности этого события. Она устанавливает факт сходимости по вероятности тех или иных случайных величин к постоянным, не случайным величинам.

Краткая теория:

Теорема Я. Бернулли: при увеличении количества опытов, частота появлений событий сходится по вероятности к вероятности этого события.

где , - сколь угодно малые положительные числа.

Вероятность того, что в n независимых испытаний, в которых вероятность появления события равна р(0<р<1), событие наступит ровно к раз(безразлично, в какой последовательности), равна

, или

где q=1-p

Вероятность того, что в n испытаниях событие наступит:

a)  менее к раз;

b)  более к раз;

c)  не менее к раз;

d)  не более к раз; - находятся по формулам:

a)  ;

b)  ;

c)  ;

d)  .

Теорема Я. Бернулли утверждает устойчивость частоты при постоянных условиях опыта. Но при изменяющихся условиях опыта аналогичная устойчивость также существует. Теорема, устанавливающая свойство устойчивости частот при переменных условиях опыта, называется теоремой Пуассона.

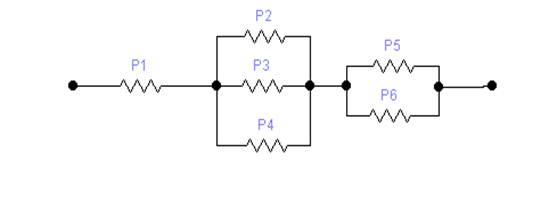
Схема цепи:

Вычисление вероятности:

Пусть вероятности безотказной работы элементов выглядят следующим образом:

P₁ = 0.5

P₂ = 0.45

P₃ = 0.6

P₄ = 0.9

P₅ = 0.39

P₆ = 0.42

P₇ = 0.6

Текст программы:

Program Shiva;

Uses CRT;

Label Start;

Const

k = 7; n = 100000;

Top = 60; Left = 55; Width = 360; Height = 380;

Type Real = Extended;

Var

GrDriver, GrMode : Integer;

R : Array[1..k] Of Record P : Real; Works : Boolean; End;

Fr : Real; j : Byte;

m, i, w : LongInt; Gone : Boolean;

Function Calc : Real;

Var P1, P2, P3, P4 : Real;

Begin

Calc := (R[1].P +R[2].P-R[1].P*R[2].P+R[3].P-R[3].P*

(R[1].P+R[2].P-R[1].P*R[2].P))*R[4].P*

(R[5].P +R[6].P-R[5].P*R[6].P+R[7].P-R[7].P*

(R[5].P+R[6].P-R[5].P*R[6].P));

End;

Procedure Init_Condit;

Var i : Byte;

Begin

For i := 1 To k Do Begin

R[i].Works := False;

If Random <= R[i].P Then R[i].Works := True;

End;

Gone := (R[1].Works Or R[2].Works Or R[3].Works)

And R[4].Works And (R[5].Works Or R[6].Works Or R[7].Works);

End;

Begin

ClrScr; Randomize;

R[1].P := 0.5; R[2].P := 0.45; R[3].P := 0.6; R[4].P := 0.9;

R[5].P := 0.39; R[6].P := 0.42; R[7].P := 0.6;

WriteLn; WriteLn(' Расчетная вероятность: ', Calc:0:3); WriteLn;

WriteLn(' n p*'); WriteLn; m := 0; w := 0;

For j := 1 To 18 Do Begin

For i := 1 To 1000 Do Begin

Inc(w);

Init_Condit;

If Gone Then Inc(m);

End; Fr := m / w;

WriteLn(w : 10, Fr:15:3);

End;

Repeat Until KeyPressed;

End.

Результаты программы:

Расчетная вероятность: 0.688

N,числоопытов	p*,частота
1000	0.675
2000	0.678
3000	0.676
4000	0.680
5000	0.681
6000	0.682
7000	0.684
8000	0.683
9000	0.683
10000	0.684
11000	0.685
12000	0.685
13000	0.685
14000	0.686
15000	0.687
16000	0.687
17000	0.687
18000	0.688

Проверка в ручную:

Первый способ:

 

Вывод: при большом числе опытов частота события приближается (точнее - сходится по вероятности) к вероятности этого события. Следовательно, можно сделать вывод, что теорема Бернулли верна.

Задание 2,3. Моделирование дискретной случайной величины, имеющей закон распределения Пуассона. Подтверждение гипотезы о том, что полученная случайная величина имеет данный закон распределения с помощью критерия Колмогорова.

Закон Пуассона

Рассмотрим случайную величину X, которая может принимать целые, неотрицательные значения:0,1,2,... ,m,...

Говорят, что эта СВ X распределена по закону Пуассона, если вероятность того, что она примет определенное значение т, выражается формулой:

(m=0,1,2...), а - некоторая положительная величина называемая параметром закона Пуассона. Ряд распределения СВ X, распределенный по закону Пуассона, имеет вид:

	0	1	2	…	m	…
		(a/1!)	(а2/2!)	…	(am/m!)	…

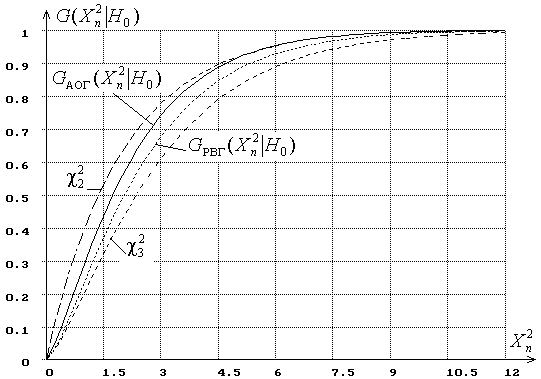
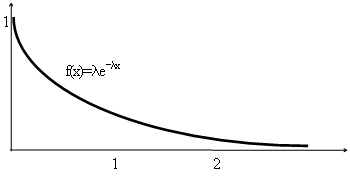
Это распределение зависит от одного параметра а, на рисунке 1 показан вид распределения Пуассона при различных а.

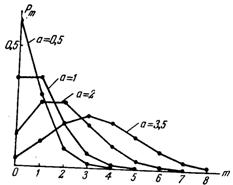
Математическое ожидание данного распределения случайной величины равно параметру закона Пуассона а: ; Дисперсия также равна этому параметру: D_x=a. Таким образом дисперсия случайной величины, распределенной по закону Пуассона равна ее математическому ожиданию и равна параметру а.

Это свойство применяется на практике для решения вопроса, правдоподобна ли гипотеза о том, что случайная величина X, распределена по закону Пуассона, для этого определяют из опыта статистические характеристики: математическое ожидание и дисперсию. Если их значения близки, то гипотеза является правдоподобной.

Дискетной называется случайная величина возможные значения которой есть отдельные изолированные числа(т.е. между двумя возможными соседними значениями нет возможных значений), которые эта величина принимает с определенными вероятностями. Другими словами, возможные значения дискретной случайной величины можно перенумеровать. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (в последнем случае множество всех возможных значений называют счетным).

Законом распределения называют перечень ее возможных значений и соответствующих им вероятностей. Текст программы:

Program Puasson_Kolmagor;

Uses CRT, Graph;

Const a = 2.0; d = 8; n = 500; k = d+1; Lkr = 1.2;

Top = 68; Left = 45; Width = 550; Height = 340; Ny = 14;

Type Real = Extended;

Var GrDriver, GrMode, X1, Y1, X2, Y2 : Integer;

i, j, w : Word; SumS, SumA, Ran, Dk, Kol : Real;

Xmin, Xmax, Ry, Mx, Dx, Rx, Sx, Ex, Sk, h : Real;

HZoom, VZoom, Lx, Ly : Real; Txt : String[20];

S, AL, AY, Y : Array[0..d] Of Real;

X : Array[1..n] Of Byte;

Procedure Bue; Far;

Begin

AssignCrt(Output); Rewrite(Output); CloseGraph;

Window(1, 1, 80, 25); ClrScr;

WriteLn ('Programed by Yuri Melnikov RD-2');

WriteLn ('All rights reserved. (c) 2004.');

WriteLn ('Thanks for attention.');

End;

Procedure Pause;

Var TextAtt, i : Byte;

Begin

Delay(1000); While KeyPressed Do ReadKey;

TextAtt := TextAttr; TextColor(7);

GoToXY(1, 25); For i := 1 To 5 Do WriteLn;

Write(' Press any key to continue or <ESC> to exit...');

Repeat Until KeyPressed; If ReadKey = #27 Then Halt;

TextAttr := TextAtt; GoToXY(1, 1); ClearDevice;

End;

Function Pwr(x, p: Real) : Real; {Возведение в степень}

Begin

If x > 0 Then Pwr := exp(p*ln(x))

Else Pwr := 0;

End;

Function Fact(x : Word) : Real;

{Справка для Егоровой Т.П. Считает до 1000!}

Var i : Word; F : Real;

Begin

F := 1;

If x > 0 Then For i := 1 To x Do F := F * i;

Fact := F;

End;

Function f(m : Word) : Real;

Begin

If m >= 0 Then f := Pwr(a, m)*exp(-a) / Fact(m)

Else f := 0;

End;

Begin

Assign(Output, ''); Rewrite(Output); Randomize; ExitProc := @Bue;

DetectGraph(GrDriver, GrMode); InitGraph(GrDriver, GrMode, 'BGI');

SumS := 0;

For i := 0 To d Do Begin

S[i] := f(i); SumS := SumS + S[i];

 End;

For i := 0 To d Do Begin al[i] := 0;

For j := 0 To i Do al[i] := al[i] + S[j] / SumS;

End;

For w := 1 To n Do Begin

Ran := Random;

For i := 0 To d Do Begin

If al[i] > Ran Then Begin

x[w] := i; Break;

End;

End;

End; WriteLn; Write(' Смоделирована ');

WriteLn('последовательность случайных чисел (з. Пуассона):');

WriteLn; Mx := 0;

For i := 1 To n Do Begin

Write(X[i]:2, ' ');

Mx := Mx + X[i] / n;

End; Pause; Dx := 0; Sk := 0;

Xmin := X[1]; Xmax := Xmin;

For i := 1 To n Do Begin

Dx := Dx + Sqr(x[i]-Mx) / (n - 1);

If Xmin > X[i] Then Xmin := X[i];

If Xmax < X[i] Then Xmax := X[i];

End;

Sx := Sqrt(Dx); WriteLn;

Rx := d; h := Rx / k; Ex := -3;

For i := 1 To n Do Begin

Sk := Sk + Sqr(x[i]-Mx)*(x[i]-Mx)/(Dx*Sx*k);

Ex := Ex + Sqr(x[i]-Mx)*Sqr(x[i]-Mx)/(k*Sqr(Dx));

End;

 WriteLn(' Диапазон значений: ', Xmin:0:3, ' - ', Xmax:0:3);

WriteLn(' Мат. ожидание: ', Mx:0:3);

WriteLn(' Дисперсия: ', Dx:0:3);

WriteLn(' Ср. кв. отклонение: ', Sx:0:3);

WriteLn(' Коэффициент скошенности: ', Sk:0:3);

WriteLn(' Эксцесс: ', Ex:0:3); Pause;

For i := 1 To n Do Begin

j := Trunc((x[i]-Xmin) / h); If j > d Then j := d;

y[j] := y[j] + 1/n;

End; Dk := 0;

For i := 0 To d Do Begin ay[i] := 0; al[i] := 0;

For j := 0 To i Do Begin

ay[i] := ay[i] + y[j];

al[i] := al[i] + f(j);

End;

If Dk < Abs(ay[i]-al[i]) Then Dk := Abs(ay[i]-al[i]);

End; Ry := 0;

For i := 0 To d Do Begin

If Ry < y[i] Then Ry := y[i];

End;

HZoom := Width / Rx; VZoom := Height / Ry;

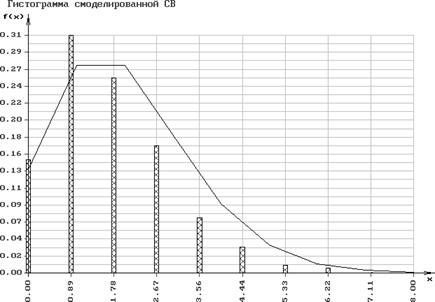
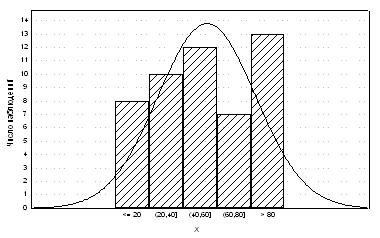
WriteLn; WriteLn(' Гистограмма смоделированной СВ :');

Lx := Rx / k; Ly := Ry / Ny; SetTextStyle(0,1,0);

SetViewPort(Left, Top, Left + Width, Top + Height, False);

For i := 0 To k Do Begin

X1 := Round(Lx*i*HZoom);

SetColor(7); Line(X1, 0, X1, Height + 5);

Str((Lx*i+Xmin):0:2, Txt);

OutTextXY(X1+4, Height+10, Txt);

SetColor(DarkGray); Line(X1, 0, X1, Height);

End; SetTextStyle(0, 0,0);

For i := 0 To Ny Do Begin

Y1 := Round(Height-Ly*i*VZoom);

SetColor(7); Line(-5, Y1, Width, Y1); Str(Ly*i:0:2, Txt);

OutTextXY(-40, Y1-4, Txt);

SetColor(DarkGray); Line(0, Y1, Width, Y1);

Y1 := Round(Height-Ly*(i-0.5)*VZoom);

If i > 0 Then Line(0, Y1, Width, Y1);

End;

SetColor(White); SetFillStyle(8, 7);

For i := 1 To k Do Begin

X1 := Round((i-1)*Lx*HZoom-Lx*HZoom*0.05);

X2 := Round(i*Lx*HZoom-Lx*HZoom*0.95);

Y1 := Round(Height - y[i-1]*VZoom); Y2 := Height;

Bar3D(X1, Y1, X2, Y2, 0, False);

End;

MoveTo(0, Round(Height-f(0)*VZoom));

For i := 1 To d Do

LineTo(Round(i*HZoom), Round(Height-f(i)*VZoom));

Line(0, -30, 0, Height+5); Line(0, -28, 2, -15); Line(0, -28, -2, -15);

Line(-5, Height, Width + 30, Height);

OutTextXY(-36,-30,'f(x)');

OutTextXY(Width+20, Height+5,'x');

Line(Width + 28, Height, Width + 15, Height-2);

Line(Width + 28, Height, Width + 15, Height+2);

Pause; WriteLn;

Kol := Dk * Sqrt(n);

WriteLn(' Критерий Колмогорова:'); WriteLn;

WriteLn(' F(x) F~(x) '); WriteLn;

For i := 0 To d Do WriteLn(al[i]:10:2, ay[i]:14:2);

WriteLn; WriteLn(' Максимум модуля разности: ', Dk:0:2);

WriteLn(' Значение лямбда: ', Kol:2:2);

WriteLn(' Лямбда критическое (а=0.1): ', Lkr:2:2);

Write(' Так как ', Kol:0:2, ' ');

If Kol < Lkr Then Begin

WriteLn('< ', Lkr:0:2, ' то расхождения можно считать случайными.');

WriteLn(' Нет оснований отвергнуть гипотезу о распределении');

Write(' данной совокупности по закону Пуассона.');

End;

If Kol > Lkr Then Begin

WriteLn('> ', Lkr:0:2, ' то расхождения следует считать неслучайными.');

WriteLn(' Нет оснований принять гипотезу о распределении');

Write(' данной совокупности по закону Пуассона.');

End;

Pause;

End.

Результаты работы программы

Смоделирована последовательность случайных чисел (з.Пуассона)

 

F(x) F^~(x)

0.14 0.15

0.41 0.45

0.68 0.71

0.86 0.88

0.95 0.95

0.98 0.98

1.00 0.99

1.00 1.00

1.00 1.00

Воспользуемся критерием Колмогорова. В качестве меры расхождения между теоретическим и статистическим распределениями рассматривается максимальное значение модуля разности между статистической функцией распределения F*(x) и соответствующей теоретической функцией распределения F(x).

D = max | F*(x)- F(x)|

D = 0.04

Далее определяем величину l по формуле:

 ,

где n – число независимых наблюдений.

Основанием для выбора в качестве меры расхождения величины D является исключительная простота её закона распределения. А.Н. Колмогоров доказал, что, какова бы ни была функция распределения F(x) непрерывной случайной велечины X, при неограниченном возрастании числа независимых наблюдении n вероятность неравенства

стремится к пределу

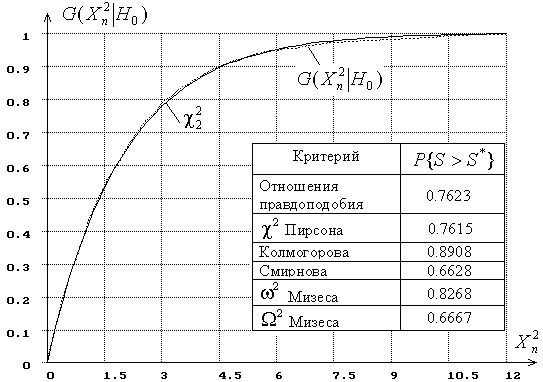
Значения вероятности , подсчитанные по формуле приведённой выше занесены в таблицу, по данной таблице находим вероятность

P(l) = 0,711.

Это есть вероятность того, что (если величина х действительно распределена по закону F(x)) за счёт чисто случайных причин максимальное расхождение между F*(x) и F(x) будет не меньше, чем наблюдаемое.

Нет оснований отвергать гипотезу о том, что наш закон распределения является геометрическим законом распределения.

Критерий Колмогорова:

F(x) F^~(x)

0.14 0.15

0.41 0.46

0.68 0.71

0.86 0.88

0.95 0.95

0.98 0.98

1.00 0.99

1.00 1.00

1.00 1.00

Список используемой литературы

1.  «Теория вероятностей» В.С. Вентцель

2.  «Теория вероятностей (Задачи и Упражнения)» В.С. Вентцель, Л.А. Овчаров

3.  «Справочник по вероятностным расчётам».

4.  «Теория вероятностей и математическая статистика» В.Е. Гмурман

5.  «Руководство к решению задач по теории вероятностей и математической статистике» В.Е. Гмурман.