Навигация
О теории вероятностей
1. Предмет и основные понятия ТВ
ТВ – математическая наука изучающая закономерность в массовых однородных случаях, явлениях и процессах.
Элементарные события – это простейшие не разложимые результаты опыта. Вся совокупность элементарных событий – пространство элементарных событий.
Под опытом в ТВ понимается выполнение некоторого комплекса условий в результате которого происходят или не происходят некоторые события – факты.
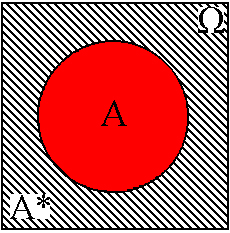
Событие в ТВ – это любое конечное или счетное подмножество пространства W.
Три типа событий:
· Достоверные
· Случайные
· Невозможные.
События являются несовместными если они не могут происходить одновременно и наоборот.
Элементы последовательность попарно несовместны, если любые два из них попарно несовместны.
Несколько событий равновозможные, если ни одно из них не имеет объективного преимущества перед другим. События образуют полную группу если в результате опыта ничего кроме этих событий не может произойти.
Алгебра событий.
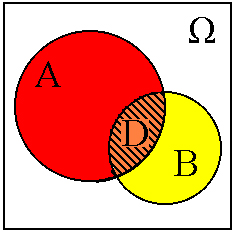
1) Суммой двух событий А + В = АÈВ называется такое третье событие которое заключается в наступлении хотя бы одного из событий А или В (или).
2) Произведением двух событий А*В = АÇВ называется такое третье событие, которое заключается в наступлении двух событий одновременно (и).
3) Отрицанием события А является событие `А, которое заключается в ненаступлении А.
4) Если наступление события А приводит к наступлению события В и наоборот, то А=В.
Пусть множество S – это множество всех подмножеств пространства всех элементов W для которых выполняются следующие условия:
1. Если АÎ S, B Î S, то A+B = AÈB Î S
2. Если АÎ S, B Î S, то А*В = АÇВ Î S
3. Если АÎ S, то `А Î S.
Тогда множество S называется алгеброй событий.
При точном подходе достаточно одного из этих свойств, так как каждое из них следует из другого.
При расширении операции сложения и умножения, на случай счетного множества событий, алгебра событий называется бролевской алгеброй.
2. Определение вероятности события.
Аксиоматическое определение вероятности.
Вероятность события – это численная мера объективной возможности его появления.
Аксиомы вероятности:
· Каждому событию А ставится в соответствие неотрицательное число р, которое называется вероятностью события А. Р(А)=р ³ 0, где АÎ S, SÍW.
· Р(W) = 1, где W - истинное (достоверное) событие.
Аксиоматический подход не указывает, как конкретно находить вероятность.
Классическое определение вероятности.
Пусть событие А1,А2, …, АnÎ S (*) образуют пространство элементарных событий, тогда событие из * которое приводит к наступлению А, называют благоприятствующими исходами для А. Вероятностью А называется отношение числа исходов благоприятствующих наступлению события А, к числу всех равновозможных элементарных исходов.
| (А)= | m(A) |
| Рn |
Свойства вероятности:
1. 0 £ Р(А) £ 1,
2. Р (W) =1,
3. Р (`W) = 0.
Статическое определение вероятности.
Пусть проводится серия опытов (n раз), в результате которых наступает или не наступает некоторое событие А (m раз), тогда отношение m/n, при n®¥ называются статистической вероятностью события А.
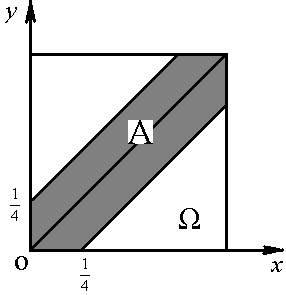
Геометрическое определение вероятности.
Геометрической вероятностью называется отношение меры области, благоприятствующей появлению события А, к мере всей области.
3. Интегральная функция распределения и ее свойства
Для непрерывной случайной величины X вероятность Р(Х= xi)→0, поэтому для НСВ удобнее использовать вероятность того, что СВ Х<хi, где хi- текущее значение переменной. Эта вероятность называется интегральной функцией распределения: P(X<xi)=F(x).
Интегральная функция является универсальным способом задания СВ (как для ДСВ, так и для НСВ).
Свойства интегральной функции распределения:
1) F(x) не убывает (если х2>x1, то F(x2)≥Р(х1));
2). F(-∞)=0;
3). F(+∞)=1;
4) вероятность попадания СВ X в интервал а<Х<b определяется по формуле
P(a≤X<b)=F(b)-F(a).
Замечание. Обычно для определённости левую границу включают в интервал, а правую нет. Вообще для НСВ верно, что
Р(а≤Х<b)= Р(а <Х≤b) =Р(а<Х < b)= Р(а≤X≤b).
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... равна 0,515). Конец 19 в. и 1-я половина 20 в. отмечены открытием большого числа статистических закономерностей в физике, химии, биологии и т.п. Возможность применения методов теории вероятностей к изучению статистических закономерностей, относящихся к весьма далёким друг от друга областям науки, основана на том, что вероятности событий всегда удовлетворяют некоторым простым соотношениям, о ...
... {ξn (ω )}¥n=1 . Поэтому, во-первых, можно говорить о знакомой из математического анализа (почти) поточечной сходимости последовательностей функций: о сходимости «почти всюду», которую в теории вероятностей называют сходимостью «почти наверное». Определение 46. Говорят, что последовательность с. в. {ξn } сходится почти наверное к с. в. ξ при n ® ¥ , и пишут: ξn ...
... ничего другого, кроме как опять же события и . Действительно, имеем: *=, *=, =, =. Другим примером алгебры событий L является совокупность из четырех событий: . В самом деле: *=,*=,=,. 2.Вероятность. Теория вероятностей изучает случайные события. Это значит, что до определенного момента времени, вообще говоря, нельзя сказать заранее о случайном событии А произойдет это событие или нет. Только ...





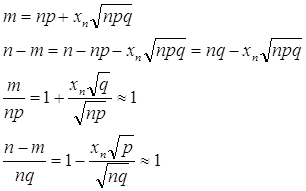
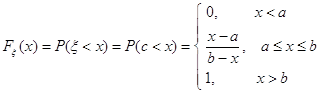
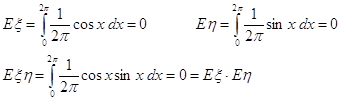
0 комментариев