САНКТ-ПЕТЕРБУРГСКИЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Кафедра «Прикладная математика»
ОТЧЕТ
ПО ВЫПОЛНЕННОЙ КУРСОВОЙ РАБОТЕ
Предмет «Численные методы»
«Применение численных методов для решения Уравнений с частными производными»
Санкт-Петербург 2008г.
Лабораторная работа N1 "Интерполирование алгебраическими многочленами"
Для решения задачи локального интерполирования алгебраическими многочленами в системе MATLAB предназначены функции polyfit (POLYnomial FITting - аппроксимация многочленом) и polyval (POLYnomial VALue - значение многочлена).
Функция polyfit (X,Y,n) находит коэффициенты многочлена степени n , построенного по данным вектора Х, который аппроксимирует данные вектора Y в смысле наименьшего квадрата отклонения. Если число элементов векторов X и Y равно n+1, то функция polyfit (X,Y,n) решает задачу интерполирования многочленом степени n.
Функция polyval (P,z) вычисляет значения полинома, коэффициенты которого являются элементами вектора P, от аргумента z . Если z – вектор или матрица, то полином вычисляется во всех точках z.
Воспользуемся указанными функциями системы MATLAB для решения задачи локального интерполирования алгебраическими многочленами функции, заданной таблицей своих значений
| X | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 |
| Y | 1.0 | 1.8 | 2.2 | 1.4 | 1.0 |
и вычисления ее приближенного значения в точке x* = 2.2 .
Задача 1 (задача локального интерполирования многочленами)
Построить интерполяционные многочлены 1-ой, 2-ой и 3-ей степени.
Вычислить их значения при x=x*.
Записать многочлены в канонической форме и построить их графики.
Решение задачи средствами системы MATLAB:
X=[0.0000 0.5000 1.0000 1.5000 2.0000 2.5000];
Y=[0.0378 0.0653 0.3789 1.0353 0.5172 0.9765];
xzv=1.61;
P1=polyfit(X(4:5),Y(4:5),1) Коэффициенты многочлена P1
P2=polyfit(X(3:5),Y(3:5),2) Коэффициенты многочлена P2
P3=polyfit(X(3:6),Y(3:6),3) Коэффициенты многочлена P3
Полученные таким образом коэффициенты интерполяционных многочленов и значения этих многочленов при x=x* :
P1 = -1.0362 2.5896
P2 = -2.3490 7.1853 -4.4574
P3 = 2.8692 -15.2604 25.8351 -13.0650
z1 = 0.9213
z2 = 1.0221
z3 = 0.9470
многочлены P1, P2, P3
P1 = -1.0362*X+2.5896
P2 = -2.3490*X2+7.1853*X+-4.4574
P3 = 2.8692*X3 -15.2604*X2 + 25.8351 + -13.0650
Для построения графиков интерполяционных многочленов следует создать векторы xi1, xi2, xi3, моделирующие интервалы (X(3):X(4)), (X(2):X(4)),(X(2):X(5)), соответственно, и вычислить значения многочленов P1, P2, P3 для элементов векторов xi1, xi2, xi3, соответственно:
xi1=X(4):0.05:X(5);
xi2=X(3):0.05:X(5);
xi3=X(3):0.05:X(6);
y1=polyval(P1,xi1);
y2=polyval(P2,xi2);
y3=polyval(P3,xi3);
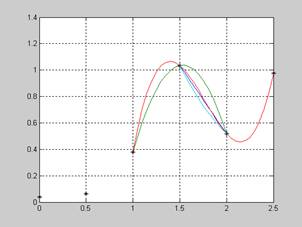
plot(X,Y,'*k',xi1,y1,xi2,y2,xi3,y3);grid
Интерполирование нелинейной функцией Y=A*exp(-B*X)
y_l=log(Y)
Pu=polyfit(X(4:5),y_l(4:5),1)
z_l=(exp(Pu(2))*exp(Pu(1)*xzv))
Y= 8.3040*exp(-1.3880*X)
Функция plot с указанными аргументами строит табличные значения функции черными звездочками('*k'), а также графики многочленов P1 (по векторам xi1 и y1), P2 (по векторам xi2 и y2) и P3 (по векторам xi3 и y3), и функцией Y=A*exp(-B*X), соответственно синей, красной и зеленой кривыми.
plot(X,Y,'*k',xi1,y1,xi2,y2,xi3,y3,xi1,exp(Pu(2))*exp(Pu(1)*xi1));grid
Оценка погрешности интерполирования
При оценке погрешности решения задачи интерполирования в точке x* за погрешность epsk интерполяционного многочлена степени k принимается модуль разности значений этого многочлена и многочлена степени k+1 в точке x*.
С помощью уже полученных значений мы можем оценить погрешности интерполяционных многочленов P1 и P2 в точке x* , используя функцию abs системы MATLAB для вычисления модуля:
eps1 = abs(z1-z2)
eps1 = 0.1008
eps2 = abs(z2-z3)
eps2 = 0.0751
Для оценки погрешности многочлена P3 необходимо предварительно вычислить
значение z4=P4(x*), а затем - eps3.
P4=polyfit(X,Y,4);z4=polyval(P4,xzv);
eps3=abs(z4-z3)
eps3 = 0.1450
«Построение сплайна»
X=[0.0000 0.5000 1.0000 1.5000 2.0000 2.5000];
Y=[0.0378 0.0653 0.3789 1.0353 0.5172 0.9765];
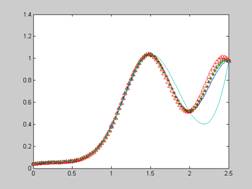
cs = spline(X,[0 Y 0]);
xx = linspace(0,2.5);
plot(X,Y,'*m',xx,ppval(cs,xx),'-k');
h=0.5
esstestvennii spline
A=[4 2 0 0 0 0
1 4 1 0 0 0
0 1 4 1 0 0
0 0 1 4 1 0
0 0 0 1 4 1
0 0 0 0 2 4]
B=[6*(Y(2)-Y(1))/h 0 0 0 0 6*(Y(length(Y))-Y(length(Y)-1))/h]
for i = 2:(length(Y)-1)
B(i)=(3/h)*(Y(i+1)-Y(i-1))
end
S=inv(A)*B'
otsutstvie uzla
A1=[1 0 -1 0 0 0
1 4 1 0 0 0
0 1 4 1 0 0
0 0 1 4 1 0
0 0 0 1 4 1
0 0 0 1 0 -1]
B1=[2*(2*Y(2)-Y(1)-Y(3))/h 0 0 0 0 2*(2*Y(length(Y)-1)-Y(length(Y))-Y(length(Y)-2))/h]
for i = 2:(length(Y)-1)
B1(i)=(3/h)*(Y(i+1)-Y(i-1))
end
S1=inv(A1)*B1'
c1 = spline(X,[S(2) Y S(5)]);
x1 = linspace(0,2.5,101);
c2 = spline(X,[S1(2) Y S1(5)]);
x2 = linspace(0,2.5,101);
plot(X,Y,'ob',xx,ppval(cs,xx),'-',x1,ppval(c1,x1),'*',x2,ppval(c2,x2),'^',xx,spline(X,Y,xx));
h = 0.5000
A =
4 2 0 0 0 0
1 4 1 0 0 0
0 1 4 1 0 0
0 0 1 4 1 0
0 0 0 1 4 1
0 0 0 0 2 4
B = 0.3300 0 0 0 0 5.5116
B = 0.3300 2.0466 0 0 0 5.5116
B = 0.3300 2.0466 5.8200 0 0 5.5116
B = 0.3300 2.0466 5.8200 0.8298 0 5.5116
B = 0.3300 2.0466 5.8200 0.8298 -0.3528 5.5116
S =
0.0052
0.1546
1.4230
-0.0266
-0.4869
1.6213
A1 =
1 0 -1 0 0 0
1 4 1 0 0 0
0 1 4 1 0 0
0 0 1 4 1 0
0 0 0 1 4 1
0 0 0 1 0 -1
B1 = -1.1444 0 0 0 0 -3.9096
B1 = -1.1444 2.0466 0 0 0 -3.9096
B1 = -1.1444 2.0466 5.8200 0 0 -3.9096
B1 = -1.1444 2.0466 5.8200 0.8298 0 -3.9096
B1 = -1.1444 2.0466 5.8200 0.8298 -0.3528 -3.9096
S1 =
0.2496
0.1008
1.3940
0.1433
-1.1372
4.0529
Лабораторная работа N2 "Построение алгебраических многочленов наилучшего среднеквадратичного приближения"
X=[0.0000 0.5000 1.0000 1.5000 2.0000 2.5000];
Y=[0.0378 0.0653 0.3789 1.0353 0.5172 0.9765];
n=length(X)
TABL=[X,sum(X);Y,sum(Y);...
X.^2,sum(X.^2);...
X.*Y,sum(X.*Y);...
X.*X.*Y,sum(X.*X.*Y);...
X.^3,sum(X.^3);X.^4,sum(X.^4)];
TABL=TABL'
X Y X^2 X*Y X^2*Y X^3 X^4
0 0.0378 0 0 0 0 0
0.5000 0.0653 0.2500 0.0326 0.0163 0.1250 0.0625
1.0000 0.3789 1.0000 0.3789 0.3789 1.0000 1.0000
1.5000 1.0353 2.2500 1.5530 2.3294 3.3750 5.0625
2.0000 0.5172 4.0000 1.0344 2.0688 8.0000 16.0000
2.5000 0.9765 6.2500 2.4413 6.1031 15.6250 39.0625
7.5000 3.0110 13.7500 5.4402 10.8966 28.1250 61.1875 - Сумма
По данным таблицы запишем и решим нормальную систему МНК-метода:
1) дл многочлена первой степени
S1=[n, TABL(7,1);TABL(7,1) TABL(7,3)] матрица коэффициентов
T1=[TABL(7,2);TABL(7,4)] вектор правых частей
coef1=S1\T1 решение нормальной системы МНК
A1=coef1(2);B1=coef1(1); коэффициенты многочлена 1-ой степени
S1 =
6.0000 7.5000
7.5000 13.7500
T1 =
3.0110
5.4402
coef1 =
0.0229
0.3832
2) дл многочлена второй степени
S2=[n TABL(7,1) TABL(7,3);TABL(7,1) TABL(7,3) TABL(7,6);TABL(7,3) TABL(7,6) TABL(7,7)] матрица коэффициентов
T2=[TABL(7,2);TABL(7,4);TABL(7,5)] вектор правых частей
coef2=S2\T2 решение нормальной системы МНК
A2=coef2(3);B2=coef2(2);C2=coef2(1); коэффициенты многочлена 2-ой степени
S2 =
6.0000 7.5000 13.7500
7.5000 13.7500 28.1250
13.7500 28.1250 61.1875
T2 =
3.0110
5.4402
10.8966
coef2 =
-0.0466
0.5917
-0.0834
Для построения графиков функций y1=A1*x+B1 и y2=A2*x^2+B2*x+C2 с найденными коэффициентами зададим вспомогательный вектор абсциссы xi, а затем вычислим элементы векторов g1=A1*xi+B1 и g2=A2*xi^2+B2*xi+C2:
h=0.05;
xi=min(X):h:max(X);
g1=A1*xi+B1;
g2=A2*xi.^2+B2*xi+C2;
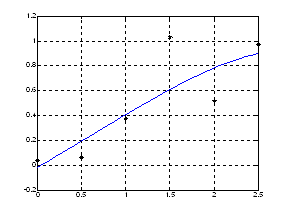
plot(X,Y,'*k',xi,g1,xi,g2);grid
coef1=polyfit(X,Y,1) коэффициенты многочлена первой степени
coef2=polyfit(X,Y,2) коэффициенты многочлена второй степени
coef1 = 0.3832 0.0229
coef2 = -0.0834 0.5917 -0.0466
Для построения графиков зададим вспомогательный вектор абсциссы xi, а затем c помощью функции polyval вычислим элементы векторов g1 и g2:
xi=min(X):0.1:max(X);
g1=polyval(coef1,xi);
g2=polyval(coef2,xi);
plot(X,Y,'*k',xi,g1,xi,g2);grid

Очевидно, что построенные таким способом графики совпадут с полученными ранее.
Для того, чтобы определить величину среднеквадратичного уклонения, вычислим суммы квадратов уклонений g1(x) и g2(x) от таблично заданной функции в узлах таблицы X а затем
G1=polyval(coef1,X);
G2=polyval(coef2,X);
delt1=sum((Y-G1).^2); delt1=sqrt(delt1/5)
delt2=sum((Y-G2).^2); delt2=sqrt(delt2/5)
Последние две строки можно заменить другими, если использовать функцию mean , вычислющую среднее значение:
delt1=mean(sum((Y-G1).^2))
delt2=mean(sum((Y-G2).^2))
delt1 = 0.2403
delt2 = 0.2335
delt1 = 0.2888
delt2 = 0.2725
Для нелинейной
X=[0.0000 0.5000 1.0000 1.5000 2.0000 2.5000];
Y=[0.0378 0.0653 0.3789 1.0353 0.5172 0.9765]
Y_o=Y
Y=1./(exp(Y))
n=length(X)
TABL=[X,sum(X);Y,sum(Y);... означает перенос строки
X.^2,sum(X.^2);...
X.*Y,sum(X.*Y);...
X.*X.*Y,sum(X.*X.*Y);...
X.^3,sum(X.^3);X.^4,sum(X.^4)];
TABL=TABL'
По данным таблицы запишем и решим нормальную систему МНК-метода:
2) дл многочлена второй степени
S2=[n TABL(7,1) TABL(7,3);TABL(7,1) TABL(7,3) TABL(7,6);TABL(7,3) TABL(7,6) TABL(7,7)] матрица коэффициентов
T2=[TABL(7,2);TABL(7,4);TABL(7,5)] вектор правых частей coef2=S2\T2 решение нормальной системы МНК
A2=coef2(3);B2=coef2(2);C2=coef2(1); коэффициенты многочлена 2-ой степени
Дл построения графиков функции y2=A2*x^2+B2*x+C2 с найденными коэффициентами зададим вспомогательный вектор абсциссы xi, а затем вычислим элементы векторов g1=A1*xi+B1 и g2=A2*xi^2+B2*xi+C2 :
h=0.05;
xi=min(X):h:max(X);
g2=log(1./(A2*xi.^2+B2*xi+C2));
plot(X,Y_o,'*k',xi,g2);grid
coef2=polyfit(X,Y,2) коэффициенты многочлена второй степени
Для построения графиков зададим вспомогательный вектор абсциссы xi, а затем c помощью функции polyval вычислим элементы векторов g1 и g2:
pause;
xi=min(X):0.1:max(X);
g2=polyval(coef2,xi);
plot(X,Y_o,'*k',xi,log(1./g2));grid
Очевидно, что построенные таким способом графики совпадут с полученными ранее.
Для того, чтобы определить величину среднеквадратичного уклонения, вычислим суммы квадратов уклонений g1(x) и g2(x) от таблично заданной функции в узлах таблицы X а затем
G2=polyval(coef2,X);
delt2=sum((Y-G2).^2); delt2=sqrt(delt2/5)
Последние две строки можно заменить другими, если использовать функцию mean , вычисляющую среднее значение:
delt2=mean(sum((Y-G2).^2))
Y = 0.0378 0.0653 0.3789 1.0353 0.5172 0.9765
Y_o = 0.0378 0.0653 0.3789 1.0353 0.5172 0.9765
Y = 0.9629 0.9368 0.6846 0.3551 0.5962 0.3766
n = 6
TABL =
0 0.9629 0 0 0 0 0
0.5000 0.9368 0.2500 0.4684 0.2342 0.1250 0.0625
1.0000 0.6846 1.0000 0.6846 0.6846 1.0000 1.0000
1.5000 0.3551 2.2500 0.5327 0.7990 3.3750 5.0625
2.0000 0.5962 4.0000 1.1924 2.3848 8.0000 16.0000
2.5000 0.3766 6.2500 0.9416 2.3539 15.6250 39.0625
7.5000 3.9122 13.7500 3.8196 6.4565 28.1250 61.1875
S2 =
6.0000 7.5000 13.7500
7.5000 13.7500 28.1250
13.7500 28.1250 61.1875
T2 =
3.9122
3.8196
6.4565
coef2 =
1.0178
-0.4243
0.0718
coef2 =
0.0718 -0.4243 1.0178
delt2 =
0.1199
delt2 =
0.0719
Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений
Эйлера явная
function dy=func(x,y)
dy=2*x*y
clear
X=[0.00000 0.10000 0.20000 0.30000 0.40000 0.50000];
Y=exp((X).^2);
Y0=input('Значение функции в точке 0 = ');
Y_n1=Y0;
for n=1:length(X)-1
Y_n1=Y_n1+0.1*2*X(n)*Y_n1;
Y_n(n)=Y_n1;
end
X1=0.00000:0.01:0.50000;
Y_sot=Y0;
for n=1:length(X1)
Y_sot=Y_sot+0.01*2*X1(n)*Y_sot;
Y_sto(n)=Y_sot;
end
X2=0.00000:0.001:0.50000;
Y_tys=Y0;
for n=1:length(X2)
Y_tys=Y_tys+0.001*2*X2(n)*Y_tys;
Y_ts(n)=Y_tys;
end
disp(' X Y h=0.1 h=0.01 h=0.001')
G1=Y_sto(10:10:end);
TABL=[X;Y;Y0,Y_n;...
Y_sto(1),G1;...
Y_ts(1),Y_ts(100:100:end)];
TABL=TABL';disp(TABL)
Значение функции в точке 0 = 1
X Y h=0.1 h=0.01 h=0.001
0 1.0000 1.0000 1.0000 1.0000
0.1000 1.0101 1.0000 1.0090 1.0099
0.2000 1.0408 1.0200 1.0387 1.0406
0.3000 1.0942 1.0608 1.0907 1.0938
0.4000 1.1735 1.1244 1.1683 1.1730
0.5000 1.2840 1.2144 1.2766 1.2833
Симметричная
clear
X=[0.00000 0.10000 0.20000 0.30000 0.40000 0.50000];
Y=exp((X).^2);
Y0=input('Значение функции в точке 0 = ');
Y_n1=Y0;
for n=1:length(X)-1
Y_n1=Y_n1*(1+0.1*X(n))/(1-0.1*(X(n)+0.1));
Y_n(n)=Y_n1;
end
X1=0.00000:0.01:0.50000;
Y_sot=Y0;
for n=1:length(X1)-1
Y_sot=Y_sot*(1+0.01*X1(n))/(1-0.01*(X1(n)+0.01));
Y_sto(n)=Y_sot;
end
X2=0.00000:0.001:0.50000;
Y_tys=Y0;
for n=1:length(X2)-1
Y_tys=Y_tys*(1+0.001*X2(n))/(1-0.001*(X2(n)+0.001));
Y_ts(n)=Y_tys;
end
disp(' X Y h=0.1 h=0.01 h=0.001')
G1=Y_sto(10:10:end);
TABL=[X;Y;Y0,Y_n;...
Y_sto(1),G1;...
Y_ts(1),Y_ts(100:100:end)];
TABL=TABL';disp(TABL)
Значение функции в точке 0 = 1
X Y h=0.1 h=0.01 h=0.001
0 1.0000 1.0000 1.0001 1.0000
0.1000 1.0101 1.0101 1.0101 1.0101
0.2000 1.0408 1.0410 1.0408 1.0408
0.3000 1.0942 1.0947 1.0942 1.0942
0.4000 1.1735 1.1745 1.1735 1.1735
0.5000 1.2840 1.2858 1.2840 1.2840
Эйлера неявная
clc
clear all
h_1=0.1;
X=0:h_1:0.5;
Y=exp(X.^2);
Yn=Y(1);
Y2=Yn+h_1*2*X(1);
или Y2=input('Введите значение Yn в точке X=0 =')
y_1(1)=Y2;
for i = 1:(length(Y)-1)
y_1(i+1)=y_1(i)/(1-h_1*2*X(i+1));
end
h_2=0.01;
X_2=0:h_2:0.5;
Y_2=exp(X_2.^2);
Y2=Yn+h_2*2*X(1);
y_2(1)=Y2;
for i = 1:(length(Y_2)-1)
y_2(i+1)=y_2(i)/(1-h_2*2*X_2(i+1));
end
h_3=0.001;
X_3=0:h_3:0.5;
Y_3=exp(X_3.^2);
Y2=Yn+h_3*2*X(1);
y_3(1)=Y2;
for i = 1:(length(Y_3)-1)
y_3(i+1)=y_3(i)/(1-h_3*2*X_3(i+1));
end
for k=1:5
r1(k)=y_2(k*10+1);
r2(k)=y_3(k*100+1);
end
TABL=[X; Y;... ... означает перенос строки
y_1;...
y_2(1),r1;...
y_3(1),r2];
TABL=TABL'
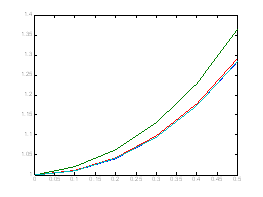
plot(X,Y,'-',X,y_1,X,[y_2(1),r1],X,[y_3(1),r2])
f=ode23('y_1',[0 0.5],1)
TABL =
0 1.0000 1.0000 1.0000 1.0000
0.1000 1.0101 1.0204 1.0111 1.0102
0.2000 1.0408 1.0629 1.0430 1.0410
0.3000 1.0942 1.1308 1.0977 1.0945
0.4000 1.1735 1.2291 1.1787 1.1740
0.5000 1.2840 1.3657 1.2916 1.2848
Задача Коши
function [ output_args ] = koshi( input_args )
KOSHI Summary of this function goes here
Detailed explanation goes here
tspan=[0,1];
y0=[1.421,1];
[t,y]=ode45(@F,tspan,y0);
ode45(@F,tspan,y0);
hold on
plot([0 1],[1 1])
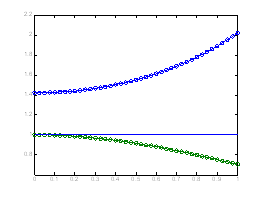
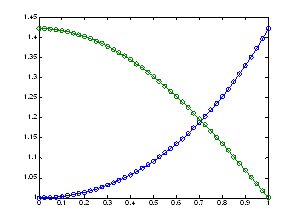
Подбор Альфа методом секущих
a=1;
y0=[1,a];
tspan=[0,1];
psi_old=a-1;
a_old=0.5;
i = 1;
eps = 1;
while (eps >= 0.000001) & (i < 10000)
[t,y]=ode45(@F,tspan,y0);
ode45(@F,tspan,y0)
psi=y(end,2)-1;
a_new=a-psi*(a-a_old)/(psi-psi_old)
eps = abs(psi);
a_old = a;
a = a_new;
y0=[1,a];
psi_old = psi
i = i + 1;
end
i
a_new = 0.5000
psi_old = -0.3935
a_new = 1.4655
psi_old = -0.8161
a_new = 1.4184
psi_old = 0.0419
a_new = 1.4215
psi_old = -0.0030
a_new = 1.4215
psi_old = -4.1359e-006
a_new = 1.4215
psi_old = 4.2046e-010
i = 7
Генерация матрицы 10*10 из элементов равномерно распределённых 1..10
function [ output_args ] = ravnomern10_10_1_10( input_args )
RAVNOMERN10_10_1_10 Summary of this function goes here
Detailed explanation goes here
round(rand(10,10)*9+1)
8 2 7 7 5 3 8 9 4 2
9 10 1 1 4 7 3 3 8 1
2 10 9 3 8 7 6 8 6 6
9 5 9 1 8 2 7 3 6 8
7 8 7 2 3 2 9 9 9 9
2 2 8 8 5 5 10 4 4 2
4 5 8 7 5 10 6 3 8 6
6 9 5 4 7 4 2 3 8 5
10 8 7 10 7 6 2 7 4 1
10 10 3 1 8 3 3 5 6 4
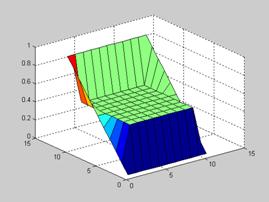
Решение краевой задачи методом сеток для УЧП.
e=0.01;
h=sqrt(e);
x=0:h:1;
y=0:h:1;
v=ones(11,11);
v(1,:)=0;
v(end,:)=1;
v(:,1)=(0:h:1)';
v(:,end)=(0:h:1)';
v=v.*((1*9+sum(0:h:1)+sum(0:h:1))/40)
v(1,:)=0;
v(end,:)=1;
v(:,1)=(0:h:1)';
v(:,end)=(0:h:1)';
surf(v);
d = e+1;
i=1
while d > e & i < 100
v1=v;
v1(1:10,:)=v1(2:11,:);
v1(11,:)=v(1,:);
v2=v;
v2(2:11,:)=v2(1:10,:);
v2(1,:)=v(11,:);
v3=v;
v3(:,1:10)=v3(:,2:11);
v3(:,11)=v(:,1);
v4=v;
v4(:,2:11)=v4(:,1:10);
v4(:,1)=v(:,11);
v_new=(v1+v2+v3+v4)/4;
d = max(max(abs(v(2:end-1,2:end-1)-v_new(2:end-1,2:end-1))))
v=v_new;
v(1,:)=0;
v(end,:)=1;
v(:,1)=(0:h:1)';
v(:,end)=(0:h:1)';
pause(0.5);
surf(v);
i = i + 1;
end;
Результат работы программы:
i = 1
d = 0.2250
d = 0.0875
d = 0.0500
d = 0.0344
d = 0.0297
d = 0.0245
d = 0.0199
d = 0.0175
d = 0.0154
d = 0.0137
d = 0.0120
d = 0.0108
d = 0.0093
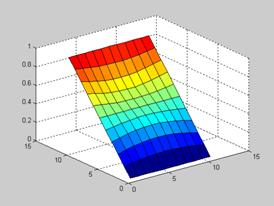
HELM ВЫЧИСЛЯЕТ МЕТОДОМ МОНТЕ-КАРЛО (АЛГОРИТМ "БЛУЖДАНИЙ ПО СЕТКЕ") РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА В ЗАДАННОЙ ТОЧКЕ (x,y) ПРЯМОУГОЛЬНОЙ ОБЛАСТИ D, ОПРЕДЕЛЕННОЙ ГРАНИЦАМИ.
Код программ:
ЗАПИС КРАЕВЫХ УСЛОВИЙ В ЗАДАЧЕ
ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
function yp=funch(x,y);
if x=0,yp=y;end;
if y=0,yp=0;end;
if y=1,yp=1;end;
if x=1,yp=y;end;
function [z1,z2,z3]=helm(c,fun,xm,ym,gr,x0,y0,h,n);
HELM ВЫЧИСЛЯЕТ МЕТОДОМ МОНТЕ-КАРЛО (АЛГОРИТМ "БЛУЖДАНИЙ ПО СЕТКЕ")
РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА В ЗАДАННОЙ
ТОЧКЕ (x,y) ПРЯМОУГОЛЬНОЙ ОБЛАСТИ D, ОПРЕДЕЛЕННОЙ ГРАНИЦАМИ
0<=x<=xm, 0<=y<=ym
(УЧП) Uxx+Uyy-c*U=F(x,y)
(ГУ) U|г=G(x,y)
Входные данные:
c - КОЭФФИЦИЕНТ (функциональный) ЛЕВОЙ ЧАСТИ УЧП;
fun - ФУНКЦИЯ F(x,y) В ПРАВОЙ ЧАСТИ УЧП (ФУНКЦИЯ ПОЛЬЗОВАТЕЛЯ);
xm,ym - ГРАНИЦЫ ПРЯМОУГОЛЬНОЙ ОБЛАСТИ;
gr - ГРАНИЧНЫЕ УСЛОВИЯ (ФУНКЦИЯ ПОЛЬЗОВАТЕЛЯ);
x0,y0 - КООРДИНАТЫ ТОЧКИ, В КОТОРОЙ ИЩЕТСЯ РЕШЕНИЕ;
h - ШАГ СЕТКИ (ЗАДАЕТСЯ ПОЛЬЗОВАТЕЛЕМ);
n - ЧИСЛО ТРАЕКТОРИЙ.
Выходные данные:
z1 - ПРИБЛИЖЕННОЕ ЗНАЧЕНИЕ РЕШЕНИЯ;
z2 - ВЕРОЯТНАЯ ОШИБКА;
z3 - ВЕРХНЯЯ ГРАНИЦА ОШИБКИ.
Обращение: [z1,z2,z3]=helm(c,fun,xm,ym,gr,x0,y0,h,n)
global z
z=[];
i0=round(x0/h);
j0=round(y0/h);
im=round(xm/h);
jm=round(ym/h);
disp(' ')
disp(' Подождите, идет расчет.')
for count=1:n,
x=x0;y=y0;
i=i0;j=j0;
q=1;
tmp=4+eval(c)*h^2;
s=h^2*eval(fun)/tmp;
while all([i,j,im-i,jm-j]),
p=[0,1/4];p=[p,p(2)];
p=[p,1/4]; p=[p,p(4)];
alf=rand;
pp=max(find(alf>cumsum(p)));
if pp==1,j=j+1;end
if pp==2,j=j-1;end
if pp==3,i=i+1;end
if pp==4,i=i-1;end
x=i*h;y=j*h;
q=q*4/tmp;
s=s+q*h^2*eval(fun)/tmp;
end
s=s+q*feval(gr,x,y);
z=[z,s];
end
disp(' ');
disp(' РЕШЕНИЕ ЗАДАЧИ:');
disp(' ============================= ');
disp(' ')
disp(' при числе траекторий');disp(n);
disp('значение в точке с координатами ');
disp(' x0 y0');
disp([x0,y0]);
z1=mean(z);disp(' ПРИБЛИЖЕННОГО РЕШЕНИЯ - ');disp(z1);
z2=0.6745*std(z)/sqrt(n);disp(' ВЕРОЯТНОЙ ОШИБКИ - ');disp(z2);
z3=z2*3/0.6745;disp(' ВЕРХНЕЙ ГРАНИЦЫ ОШИБКИ - ');disp(z3);
ОБРАЩЕНИЯ К ФУНКЦИИ HELM:
global z
c='1';
f='0';
xm=1;ym=1;
gr='funch';
x0=0.6;y0=0.7;
h=0.1;
n=600;
[z1,z2,z3]=helm(c,f,xm,ym,gr,x0,y0,h,n);
Результат работы программы:
РЕШЕНИЕ ЗАДАЧИ:
при числе траекторий 600
значение в точке с координатами x0 y0 0.6000 0.7000
ПРИБЛИЖЕННОГО РЕШЕНИЯ - 0.2958
ВЕРОЯТНОЙ ОШИБКИ - 0.0089
ВЕРХНЕЙ ГРАНИЦЫ ОШИБКИ - 0.0397
Похожие работы
... точке приближенного решения, т. е. Последовательные приближения (4) строятся по формулам: , (9) где – начальное приближение к точному решению . 4.5 Метод Зейделя на основе линеаризованного уравнения Итерационная формула для построения приближенного решения нелинейного уравнения (2) на основе линеаризованного уравнения (7) имеет вид: 4.6 Метод наискорейшего спуска Методы ...
... менять саму их постановку, вводя в нее дополнительную априорную информацию о строении решения. 2. Классификация уравнений гиперболического типа в контексте классификации уравнений математической физики Уравнения математической физики, дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные ...
... с помощью рекурентных соотношений? 104) Приведите конечно-разностные выражения для первой производной. 105) Подынтегральная функция y = f(x) задана таблицейВзяв h = 0,3, вычислить интеграл на отрезке [0,3; 0,9] методом Симпсона. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЧИСЛЕННЫЕ МЕТОДЫ Билет № 22 106) Как ...
... коэффициенты an (x1), bn (x1), an (x2), bn (x2) при помощи гармонического анализа, можно определить коэффициент температуропроводности стержня а2. Глава 3. МОДЕЛИРОВАНИЕ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ. §3.1. Дифракция излучения на сферической частице. Перейдем теперь к рассмотрению задачи о дифракции электромагнитных волн на сферической частице. Как известно, в ...
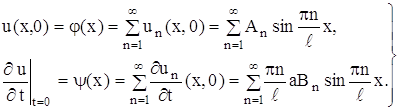
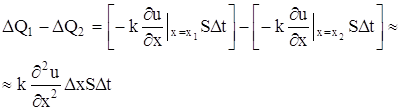
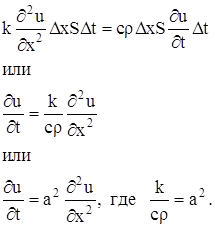
0 комментариев