Всероссийский заочный финансово-экономический институт
Лабораторная работа
по дисциплине "Эконометрика"
Брянск 2010
Задание
В таблице 1 представлены данные о рынке строящегося жилья в Санкт-Петербурге (по состоянию на декабрь 1996г.).
Таблица 1 – Исходные данные
| № п/п | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 | У |
| 1 | 1 | 1 | 39 | 20 | 8,2 | 0 | 1 | 0 | 15,9 |
| 2 | 3 | 1 | 68,4 | 40,5 | 10,7 | 0 | 1 | 0 | 27 |
| 3 | 1 | 1 | 34,8 | 16 | 10,7 | 0 | 1 | 12 | 13,5 |
| 4 | 1 | 1 | 39 | 20 | 8,5 | 0 | 1 | 12 | 15,1 |
| 5 | 2 | 1 | 54,7 | 28 | 10,7 | 0 | 1 | 12 | 21,1 |
| 6 | 3 | 1 | 74,7 | 46,3 | 10,7 | 0 | 1 | 12 | 28,7 |
| 7 | 3 | 1 | 71,7 | 45,9 | 10,7 | 0 | 0 | 0 | 27,2 |
| 8 | 3 | 1 | 74,5 | 47,5 | 10,4 | 0 | 0 | 0 | 28,3 |
| 9 | 4 | 1 | 137,7 | 87,2 | 14,6 | 0 | 1 | 0 | 52,3 |
| 10 | 1 | 1 | 40 | 17,7 | 11 | 1 | 1 | 8 | 22 |
| 11 | 2 | 1 | 53 | 31,1 | 10 | 1 | 1 | 8 | 28 |
| 12 | 3 | 1 | 86 | 48,7 | 14 | 1 | 1 | 8 | 45 |
| 13 | 4 | 1 | 98 | 65,8 | 13 | 1 | 1 | 8 | 51 |
| 14 | 2 | 1 | 62,6 | 21,4 | 11 | 1 | 1 | 0 | 34,4 |
| 15 | 1 | 1 | 45,3 | 20,6 | 10,4 | 1 | 1 | 8 | 24,7 |
| 16 | 2 | 1 | 56,4 | 29,7 | 9,4 | 1 | 1 | 8 | 30,8 |
| 17 | 1 | 1 | 37 | 17,8 | 8,3 | 0 | 1 | 0 | 15,9 |
| 18 | 3 | 1 | 67,5 | 43,5 | 8,3 | 0 | 1 | 0 | 29 |
| 19 | 1 | 1 | 37 | 17,8 | 8,3 | 0 | 1 | 3 | 15,4 |
| 20 | 3 | 1 | 69 | 42,4 | 8,3 | 0 | 1 | 3 | 28,6 |
| 21 | 1 | 1 | 40 | 20 | 8,3 | 0 | 0 | 0 | 15,6 |
| 22 | 3 | 1 | 69,1 | 41,3 | 8,3 | 0 | 1 | 0 | 27,7 |
| 23 | 2 | 1 | 38,1 | 35,4 | 13 | 1 | 1 | 20 | 34,1 |
| 24 | 2 | 1 | 75,3 | 41,4 | 12,1 | 1 | 1 | 20 | 37,7 |
| 25 | 3 | 1 | 83,7 | 48,5 | 12,1 | 1 | 1 | 20 | 41,9 |
| 26 | 1 | 1 | 48,7 | 22,3 | 12,4 | 1 | 1 | 20 | 24,4 |
| 27 | 1 | 1 | 39,9 | 18 | 8,1 | 1 | 0 | 0 | 21,3 |
| 28 | 2 | 1 | 68,6 | 35,5 | 17 | 1 | 1 | 12 | 36,7 |
| 29 | 1 | 1 | 39 | 20 | 9,2 | 1 | 0 | 0 | 21,5 |
| 30 | 2 | 1 | 48,6 | 31 | 8 | 1 | 0 | 0 | 26,4 |
| 31 | 3 | 1 | 98 | 56 | 22 | 1 | 0 | 0 | 53,9 |
| 32 | 2 | 1 | 68,5 | 30,7 | 8,3 | 1 | 1 | 6 | 34,2 |
| 33 | 2 | 1 | 71,1 | 36,2 | 13,3 | 1 | 1 | 6 | 35,6 |
| 34 | 3 | 1 | 68 | 41 | 8 | 1 | 1 | 12 | 34 |
| 35 | 1 | 1 | 38 | 19 | 7,4 | 1 | 1 | 12 | 19 |
| 36 | 2 | 1 | 93,2 | 49,5 | 14 | 1 | 1 | 12 | 46,6 |
| 37 | 3 | 1 | 117 | 55,2 | 25 | 1 | 1 | 12 | 58,5 |
| 38 | 1 | 2 | 42 | 21 | 10,2 | 1 | 0 | 12 | 24,2 |
| 39 | 2 | 2 | 62 | 35 | 11 | 1 | 0 | 12 | 35,7 |
| 40 | 3 | 2 | 89 | 52,3 | 11,5 | 1 | 1 | 12 | 51,2 |
| 41 | 4 | 2 | 132 | 89,6 | 11 | 1 | 1 | 12 | 75,9 |
| 42 | 1 | 2 | 40,8 | 19,2 | 10,1 | 1 | 1 | 6 | 21,2 |
| 43 | 2 | 2 | 59,2 | 31,9 | 11,2 | 1 | 1 | 6 | 30,8 |
| 44 | 3 | 2 | 65,4 | 38,9 | 9,3 | 1 | 1 | 6 | 34 |
| 45 | 2 | 2 | 60,2 | 36,3 | 10,9 | 1 | 1 | 12 | 31,9 |
| 46 | 3 | 2 | 82,2 | 49,7 | 13,8 | 1 | 1 | 12 | 43,6 |
| 47 | 3 | 2 | 98,4 | 52,3 | 15,3 | 1 | 1 | 12 | 52,2 |
| 48 | 3 | 3 | 76,7 | 44,7 | 8 | 1 | 1 | 0 | 43,1 |
| 49 | 1 | 3 | 38,7 | 20 | 10,2 | 1 | 1 | 6 | 25 |
| 50 | 2 | 3 | 56,4 | 32,7 | 10,1 | 1 | 1 | 6 | 35,2 |
| 51 | 3 | 3 | 76,7 | 44,7 | 8 | 1 | 1 | 6 | 40,8 |
| 52 | 1 | 3 | 38,7 | 20 | 10,2 | 1 | 0 | 0 | 18,2 |
| 53 | 1 | 3 | 41,5 | 20 | 10,2 | 1 | 1 | 0 | 20,1 |
| 54 | 2 | 3 | 48,8 | 28,5 | 8 | 1 | 0 | 0 | 22,7 |
| 55 | 2 | 3 | 57,4 | 33,5 | 10,1 | 1 | 1 | 0 | 27,6 |
| 56 | 3 | 3 | 76,7 | 44,7 | 8 | 1 | 1 | 0 | 36 |
| 57 | 1 | 4 | 37 | 17,5 | 8,3 | 0 | 1 | 7 | 17,8 |
| 58 | 2 | 4 | 54 | 30,5 | 8,3 | 0 | 1 | 7 | 25,9 |
| 59 | 3 | 4 | 68 | 42,5 | 8,3 | 0 | 1 | 7 | 32,6 |
| 60 | 1 | 4 | 40,5 | 16 | 11 | 0 | 1 | 3 | 19,8 |
| 61 | 2 | 4 | 61 | 31 | 11 | 0 | 1 | 3 | 29,9 |
| 62 | 3 | 4 | 80 | 45,6 | 11 | 0 | 1 | 3 | 39,2 |
| 63 | 1 | 3 | 52 | 21,2 | 11,2 | 1 | 1 | 18 | 22,4 |
| 64 | 2 | 3 | 78,1 | 40 | 11,6 | 1 | 1 | 18 | 35,2 |
| 65 | 3 | 3 | 91,6 | 53,8 | 16 | 1 | 0 | 18 | 41,2 |
| 66 | 1 | 4 | 39,9 | 19,3 | 8,4 | 0 | 1 | 6 | 17,8 |
| 67 | 2 | 4 | 56,2 | 31,4 | 11,1 | 0 | 1 | 6 | 25 |
| 68 | 3 | 4 | 79,1 | 42,4 | 15,5 | 0 | 1 | 6 | 35,2 |
| 69 | 4 | 4 | 91,6 | 55,2 | 9,4 | 0 | 1 | 6 | 40,8 |
Принятые в таблице обозначения:
Y – цена квартиры, тыс.долл.;
Х1 – число комнат в квартире;
Х2 – район города (1 – Приморский, Шувалово-Озерки, 2 – Гражданка, 3 – Юго-запад, 4 - Красносельский);
Х3 – общая площадь квартиры (м2);
Х4 – жилая площадь квартиры (м2);
Х5 – площадь кухни (м2);
Х6 – тип дома (1 – кирпичный, 0 - другой);
Х7 – наличие балкона (1 – есть, 0 - нет);
Х8 – число месяцев до окончания срока строительства.
1) Введите фиктивную переменную z, отражающую местоположение квартиры и позволяющую разделить всю совокупность квартир на две группы: квартиры на севере города (Приморский район, Шувалово-Озерки, Гражданка) и на юге города (Юго-запад, Красносельский район).
2) Составьте матрицу парных коэффициентов корреляции исходных переменных. Вместо переменной х2 используйте фиктивную переменную z.
3) Постройте уравнение регрессии, характеризующее зависимость цены от всех факторов в линейной форме. Установите, какие факторы мультиколлинеарны.
4) Постройте модель у = f(х3, х6, х7, х8, z) в линейной форме. Какие факторы значимо воздействуют на формирование цены квартиры в этой модели?
5) Существует ли разница в ценах на квартиры, расположенных в северной и южной частях Санкт-Петербурга?
6) Оцените статистическую значимость параметров регрессионной модели с помощью t-критерия Стьюдента; нулевую гипотезу о значимости уравнения регрессии проверьте с помощью F-критерия Фишера; оцените качество уравнения регрессии с помощью коэффициента детерминации R2.
Решение
1) Введем фиктивную переменную Z вместо Х2, отражающую местоположение квартиры и позволяющую разделить всю совокупность квартир на две группы. Первые 47 квартир относятся к северной части города (Приморский район, Шувалово-Озерки, Гражданка), а оставшиеся 22 квартиры относятся к южной части города (Юго-запад, Красносельский район). Составим матрицу парных коэффициентов корреляции исходных переменных.
| Х1 | Z | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 | У |
| 1 | 1 | 39 | 20 | 8,2 | 0 | 1 | 0 | 15,9 |
| 3 | 1 | 68,4 | 40,5 | 10,7 | 0 | 1 | 0 | 27 |
| 1 | 1 | 34,8 | 16 | 10,7 | 0 | 1 | 12 | 13,5 |
| 1 | 1 | 39 | 20 | 8,5 | 0 | 1 | 12 | 15,1 |
| 2 | 1 | 54,7 | 28 | 10,7 | 0 | 1 | 12 | 21,1 |
| 3 | 1 | 74,7 | 46,3 | 10,7 | 0 | 1 | 12 | 28,7 |
| 3 | 1 | 71,7 | 45,9 | 10,7 | 0 | 0 | 0 | 27,2 |
| 3 | 1 | 74,5 | 47,5 | 10,4 | 0 | 0 | 0 | 28,3 |
| 4 | 1 | 137,7 | 87,2 | 14,6 | 0 | 1 | 0 | 52,3 |
| 1 | 1 | 40 | 17,7 | 11 | 1 | 1 | 8 | 22 |
| 2 | 1 | 53 | 31,1 | 10 | 1 | 1 | 8 | 28 |
| 3 | 1 | 86 | 48,7 | 14 | 1 | 1 | 8 | 45 |
| 4 | 1 | 98 | 65,8 | 13 | 1 | 1 | 8 | 51 |
| 2 | 1 | 62,6 | 21,4 | 11 | 1 | 1 | 0 | 34,4 |
| 1 | 1 | 45,3 | 20,6 | 10,4 | 1 | 1 | 8 | 24,7 |
| 2 | 1 | 56,4 | 29,7 | 9,4 | 1 | 1 | 8 | 30,8 |
| 1 | 1 | 37 | 17,8 | 8,3 | 0 | 1 | 0 | 15,9 |
| 3 | 1 | 67,5 | 43,5 | 8,3 | 0 | 1 | 0 | 29 |
| 1 | 1 | 37 | 17,8 | 8,3 | 0 | 1 | 3 | 15,4 |
| 3 | 1 | 69 | 42,4 | 8,3 | 0 | 1 | 3 | 28,6 |
| 1 | 1 | 40 | 20 | 8,3 | 0 | 0 | 0 | 15,6 |
| 3 | 1 | 69,1 | 41,3 | 8,3 | 0 | 1 | 0 | 27,7 |
| 2 | 1 | 38,1 | 35,4 | 13 | 1 | 1 | 20 | 34,1 |
| 2 | 1 | 75,3 | 41,4 | 12,1 | 1 | 1 | 20 | 37,7 |
| 3 | 1 | 83,7 | 48,5 | 12,1 | 1 | 1 | 20 | 41,9 |
| 1 | 1 | 48,7 | 22,3 | 12,4 | 1 | 1 | 20 | 24,4 |
| 1 | 1 | 39,9 | 18 | 8,1 | 1 | 0 | 0 | 21,3 |
| 2 | 1 | 68,6 | 35,5 | 17 | 1 | 1 | 12 | 36,7 |
| 1 | 1 | 39 | 20 | 9,2 | 1 | 0 | 0 | 21,5 |
| 2 | 1 | 48,6 | 31 | 8 | 1 | 0 | 0 | 26,4 |
| 3 | 1 | 98 | 56 | 22 | 1 | 0 | 0 | 53,9 |
| 2 | 1 | 68,5 | 30,7 | 8,3 | 1 | 1 | 6 | 34,2 |
| 2 | 1 | 71,1 | 36,2 | 13,3 | 1 | 1 | 6 | 35,6 |
| 3 | 1 | 68 | 41 | 8 | 1 | 1 | 12 | 34 |
| 1 | 1 | 38 | 19 | 7,4 | 1 | 1 | 12 | 19 |
| 2 | 1 | 93,2 | 49,5 | 14 | 1 | 1 | 12 | 46,6 |
| 3 | 1 | 117 | 55,2 | 25 | 1 | 1 | 12 | 58,5 |
| 1 | 1 | 42 | 21 | 10,2 | 1 | 0 | 12 | 24,2 |
| 2 | 1 | 62 | 35 | 11 | 1 | 0 | 12 | 35,7 |
| 3 | 1 | 89 | 52,3 | 11,5 | 1 | 1 | 12 | 51,2 |
| 4 | 1 | 132 | 89,6 | 11 | 1 | 1 | 12 | 75,9 |
| 1 | 1 | 40,8 | 19,2 | 10,1 | 1 | 1 | 6 | 21,2 |
| 2 | 1 | 59,2 | 31,9 | 11,2 | 1 | 1 | 6 | 30,8 |
| 3 | 1 | 65,4 | 38,9 | 9,3 | 1 | 1 | 6 | 34 |
| 2 | 1 | 60,2 | 36,3 | 10,9 | 1 | 1 | 12 | 31,9 |
| 3 | 1 | 82,2 | 49,7 | 13,8 | 1 | 1 | 12 | 43,6 |
| 3 | 1 | 98,4 | 52,3 | 15,3 | 1 | 1 | 12 | 52,2 |
| 3 | 0 | 76,7 | 44,7 | 8 | 1 | 1 | 0 | 43,1 |
| 1 | 0 | 38,7 | 20 | 10,2 | 1 | 1 | 6 | 25 |
| 2 | 0 | 56,4 | 32,7 | 10,1 | 1 | 1 | 6 | 35,2 |
| 3 | 0 | 76,7 | 44,7 | 8 | 1 | 1 | 6 | 40,8 |
| 1 | 0 | 38,7 | 20 | 10,2 | 1 | 0 | 0 | 18,2 |
| 1 | 0 | 41,5 | 20 | 10,2 | 1 | 1 | 0 | 20,1 |
| 2 | 0 | 48,8 | 28,5 | 8 | 1 | 0 | 0 | 22,7 |
| 2 | 0 | 57,4 | 33,5 | 10,1 | 1 | 1 | 0 | 27,6 |
| 3 | 0 | 76,7 | 44,7 | 8 | 1 | 1 | 0 | 36 |
| 1 | 0 | 37 | 17,5 | 8,3 | 0 | 1 | 7 | 17,8 |
| 2 | 0 | 54 | 30,5 | 8,3 | 0 | 1 | 7 | 25,9 |
| 3 | 0 | 68 | 42,5 | 8,3 | 0 | 1 | 7 | 32,6 |
| 1 | 0 | 40,5 | 16 | 11 | 0 | 1 | 3 | 19,8 |
| 2 | 0 | 61 | 31 | 11 | 0 | 1 | 3 | 29,9 |
| 3 | 0 | 80 | 45,6 | 11 | 0 | 1 | 3 | 39,2 |
| 1 | 0 | 52 | 21,2 | 11,2 | 1 | 1 | 18 | 22,4 |
| 2 | 0 | 78,1 | 40 | 11,6 | 1 | 1 | 18 | 35,2 |
| 3 | 0 | 91,6 | 53,8 | 16 | 1 | 0 | 18 | 41,2 |
| 1 | 0 | 39,9 | 19,3 | 8,4 | 0 | 1 | 6 | 17,8 |
| 2 | 0 | 56,2 | 31,4 | 11,1 | 0 | 1 | 6 | 25 |
| 3 | 0 | 79,1 | 42,4 | 15,5 | 0 | 1 | 6 | 35,2 |
| 4 | 0 | 91,6 | 55,2 | 9,4 | 0 | 1 | 6 | 40,8 |
2) Проведем корреляционный анализ на выявление зависимости Y от представленных факторов в среде "СтатЭксперт".
Протокол корреляционного анализа
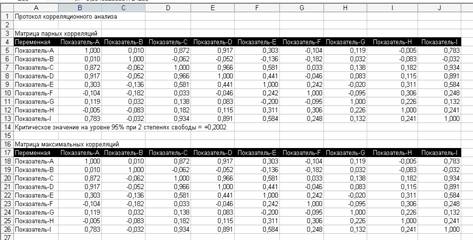
Главная цель анализа данных состоит в выявлении корреляционной связи зависимой переменной Y с независимыми переменными Хi, а также выявление независимых переменных, имеющих высокий уровень корреляции между собой.
Критическое значение коэффициента корреляции rкр = 0,2002. Это означает, что все коэффициенты корреляции, значения которых меньше rкр принимаются равными нулю, а связь между этими параметрами считается незначимой.
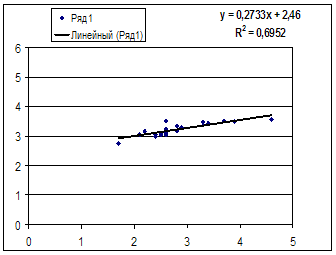
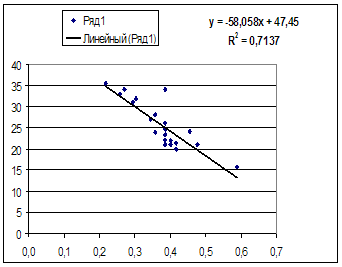
Влияние независимой переменной Х3, Х4, включенной в исследование, имеет высокий уровень (r > 0,7), причем это влияние положительно (rух3 = 0,872, rух4 = 0,917).
Х5 оказывает умеренное положительное влияние на величину Y (rух5 = 0,303).
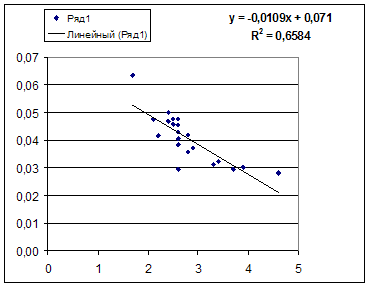
Х1, Х2, Х6, Х7, Х8 не оказывают влияния на величину Y (rух2 = 0,010, rух6 = = -0,104, rух7 = 0,119, rух8 = -0,005).
3) Построим уравнение регрессии, характеризующее зависимость цены от всех факторов, в линейной форме.
Линейная регрессия
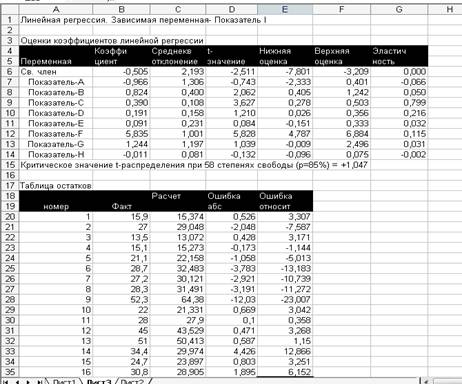
Уравнение будет иметь вид:
у(х) = -0,505 – 0,966х1 + 0,824х2 + 0,390х3 + 0,191х4 + 0,091х5 + 5,835х6 + 1,244х7 – 0,011х8
Линейная или близкая к ней связь между факторами называется мультиколлинеарностью. Считают явление мультиколлинеарности в исходных данных установленным, если коэффициент парной корреляции между двумя переменными больше 0,7.
Рассмотрим матрицу парных коэффициентов корреляции между факторами Хj, включенными в дальнейшем анализ.
Матрица парных корреляций
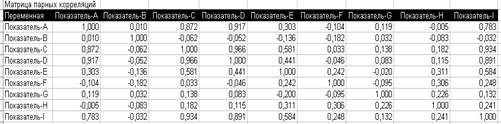
Явление сильной коллинеарности наблюдается между факторами:
Х1 и Х3, т.к. rх1х3 = 0,872 > 0,7
Х1 и Х4, т.к. rх1х4 = 0,917 > 0,7
Х3 и Х4, т.к. rх3х4 = 0,966 > 0,7
4) Построим модель у = f (х3, х6, х7, х8, z) в линейной форме.
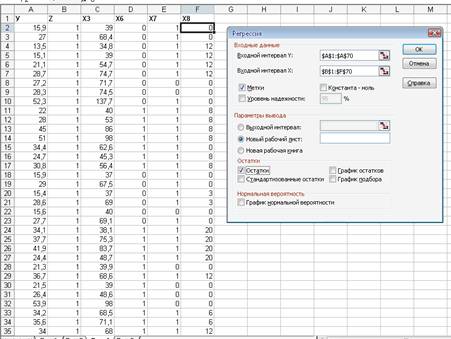
Результаты регрессионного анализа
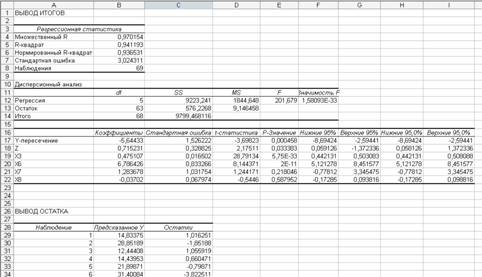
Модель в линейной форме будет иметь вид:
у(х) = -5,64 + 0,715х2 + 0,475х3 + 6,786х6 + 1,284х7 – 0,037х8
Х6 (тип дома), значимо воздействует на формирование цены квартиры в модели.
5) Оценим статистическую значимость параметров регрессионной модели с помощью t-критерия; нулевую гипотезу о значимости уравнения регрессии проверим с помощью F-критерия; оценим качество уравнения регрессии с помощью коэффициента детерминации R2.
Характеристика остатков линейной регрессии
| Характеристика | Значение |
| Среднее значение | 0,000 |
| Дисперсия | 10,579 |
| Приведенная дисперсия | 12,220 |
| Средний модуль остатков | 2,237 |
| Относительная ошибка | 7,144 |
| Критерий Дарбина-Уотсона | 1,154 |
| Коэффициент детерминации | 0,991 |
| F - значение ( n1 = 8, n2 = 58) | 764,697 |
| Критерий адекватности | 36,993 |
| Критерий точности | 47,492 |
| Критерий качества | 44,867 |
| Уравнение значимо с вероятностью 0.95 | |
Коэффициент детерминации показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, около 99,1% вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов.
Табличное значение F-критерия (Fкрит) при доверительной вероятности 0,95 при n1 = 8 и n2 = 58 составляет 2,10. Проверка гипотезы о значимости уравнения регрессии проводится на основании:
если Fфакт > Fкрит, то модель статистически значима;
если Fфакт < Fкрит, то модель статистически незначима.
Fфакт > Fкрит, значит модель статистически значима, т.е. пригодна к использованию.
Оценим с помощью t-критерия Стьюдента статистическую значимость коэффициентов уравнения регрессии.
Табличное значение t-критерия при 5% уровне значимости и степени свободы k = 69-8-1 = 60 составляет 2,0003.
Если tрасч > tтабл, то коэффициент статистически значим.
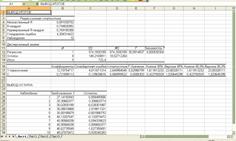
Характеристика модели
| Коэффициенты | Стандартная ошибка | t-статистика | |
| Y-пересечение | -6,10491 | 1,867676003 | -3,268720937 |
| Переменная Х 1 | -0,16426 | 1,096321271 | -0,149825399 |
| Переменная Х 2 | 0,744173 | 0,335026167 | 2,221237839 |
| Переменная Х 3 | 0,36827 | 0,092869614 | 3,965447278 |
| Переменная Х 4 | 0,147869 | 0,132602783 | 1,115126788 |
| Переменная Х 5 | 0,177213 | 0,195399452 | 0,906925347 |
| Переменная Х 6 | 6,93635 | 0,869661345 | 7,975921084 |
| Переменная Х 7 | 1,777648 | 1,124095736 | 1,581402513 |
| Переменная Х 8 | -0,04802 | 0,072432334 | -0,662966567 |
tb0 = 3,2687 > 2,0003 => коэффициент регрессии b0 статистически значим;
tb1 = 0,1498 < 2,0003 => коэффициент регрессии b0 статистически незначим;
tb2 = 2,2212 > 2,0003 => коэффициент регрессии b0 статистически значим;
tb3 = 3,9654 > 2,0003 => коэффициент регрессии b0 статистически значим;
tb4 = 1,1151 < 2,0003 => коэффициент регрессии b0 статистически незначим;
tb5 = 0,9069 < 2,0003 => коэффициент регрессии b0 статистически незначим;
tb6 = 7,9759 > 2,0003 => коэффициент регрессии b0 статистически значим;
tb7 = 1,5814 < 2,0003 => коэффициент регрессии b0 статистически незначим;
tb7 = 0,6630 < 2,0003 => коэффициент регрессии b0 статистически незначим;
6) существует ли разница в ценах на квартиры, расположенных в северной и южной частях Санкт-Петербурга?
tb2 = 2,2212 > 2,0003, tb3 = 3,9654 > 2,0003 и tb6 = 7,9759 > 2,0003,
значит факторы Х2 (район города), Х3 (общая площадь квартиры) и Х6 (тип дома) значимо влияют на формирование цен на квартиры.
Анализ показал, что разница в ценах на квартиры, расположенные в северной и южной частях Санкт-Петербурга существенна, т.к. tb2 = 2,2212 > 2,0003.
Похожие работы
... 44 72,25 =490,50 для уровня значимости 0,05 и числа степеней свободы n-2=8 Так как и можно сделать вывод, что оба коэффициента регрессии значимые. 5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера , найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели. Коэффициент детерминации определяется по ...
... поле корреляции и сформулируйте гипотезу о форме связи. 2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий. 3. Оцените тесноту связи с помощью показателей корреляции и детерминации. 4. С помощью среднего (общего) коэффициента эластичности дайте сравнительную ...
нты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод. Решение 1. Уравнение линейной регрессии имеет вид: = а0 + а1x. Построим линейную модель. Для удобства выполнения расчетов предварительно упорядочим всю таблицу исходных данных по возрастанию факторной переменной Х (Данные => Сортировка). ( ...
... 7,33 1965 81,0 7,52 1966 83,0 7,62 1967 85,4 7,72 1968 85,9 7,89 1969 85,9 7,98 1970 87,0 8,03 1971 90,2 8,21 1972 92,6 8,53 1973 95,0 8,55 1974 93,3 8,28 1975 95,5 8,12 Найдем параметры линейного уравнения множественной регрессии и значения остатков. Дополним таблицу данных столбцами "", "Квадрат разности остатков " и "Квадрат остатка " и заполним их. Таблица ...
0 комментариев