Навигация
Линейные уравнения парной и множественной регрессии
НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
"ВОЛГОГРАДСКИЙ ИНСТИТУТ БИЗНЕСА"
Кафедра
Математики и естественных наук
Домашняя контрольная работа
Дисциплина
Эконометрика
Тема: Линейные уравнения парной регрессии
Студента (ки)
Иванова Ивана Ивановича
Волгоград 2010
Задача№ 1
По данным приведенным в таблице:
1) построить линейное уравнение парной регрессии y на x;
2) рассчитать линейный коэффициент парной корреляции и оценить тесноту связи;
3) оценить статистическую значимость параметров регрессии и корреляции, используя F-статистику, t-статистику Стьюдента и путем расчета доверительных интервалов каждого из показателей;
4) вычислить прогнозное значение y при прогнозном значении x, составляющем 108% от среднего уровня.
5) оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал;
6) полученные результаты изобразить графически и привести экономическое обоснование.
Таблица №1
По территориям Центрального района известны данные за 1995 г.
| Район | Средний размер назначенных ежемесячных пенсий, тыс.руб., y | Прожиточный минимум в среднем на одного пенсионера в месяц, тыс.руб., х |
| Брянская обл. | 240 | 178 |
| Владимирская обл. | 226 | 202 |
| Ивановская обл. | 221 | 197 |
| Калужская обл. | 226 | 201 |
| Костромская обл. | 220 | 189 |
| Московская обл. | 237 | 215 |
| Орловская обл. | 232 | 166 |
| Рязанская обл. | 215 | 199 |
| Смоленская обл. | 220 | 180 |
| Тульская обл. | 231 | 186 |
| Ярославская обл. | 229 | 250 |
| xi | 178 | 202 | 197 | 201 | 189 | 215 | 166 | 199 | 180 | 186 | 250 |
| yi | 240 | 226 | 221 | 226 | 220 | 237 | 232 | 215 | 220 | 231 | 229 |
| Х | Y |
| 178 | 240 |
| 202 | 226 |
| 197 | 221 |
| 201 | 226 |
| 189 | 220 |
| 215 | 237 |
| 166 | 232 |
| 199 | 215 |
| 180 | 220 |
| 186 | 231 |
| 250 | 229 |
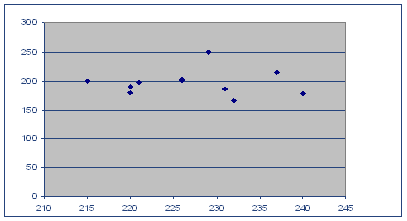
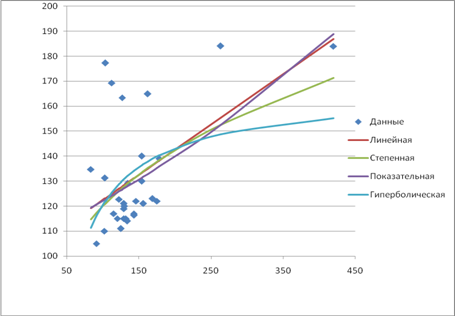
Вывод 1. Анализ корреляционного поля данных показывает, что между признаками ![]() и
и ![]() в выборочной совокупности существует прямая и достаточно тесная связь. Предполагается, что объясняемая переменная
в выборочной совокупности существует прямая и достаточно тесная связь. Предполагается, что объясняемая переменная ![]() линейно зависит от фактора
линейно зависит от фактора ![]() , поэтому уравнение регрессии будем искать в виде
, поэтому уравнение регрессии будем искать в виде
![]() ,
,
Таблица № 4 Параметры (коэффициенты) уравнения регрессии
| Коэффициенты | |
| Y-пересечение | 227,7117993 |
| Переменная X 1 | -0,003619876 |
На основании этих данных запишем уравнение регрессии: ![]() .
.
Коэффициент ![]() называется выборочным коэффициентом регрессии
называется выборочным коэффициентом регрессии ![]() Коэффициент регрессии
Коэффициент регрессии ![]() показывает, на сколько единиц в среднем изменяется переменная
показывает, на сколько единиц в среднем изменяется переменная ![]() при увеличении переменной
при увеличении переменной ![]() на одну единицу.
на одну единицу.
Таблица №5. Корреляционная матрица
| Столбец 1 | Столбец 2 | |
| Столбец 1 | 1 | |
| Столбец 2 | -0,010473453 | 1 |
Для оценки качества уравнения регрессии в целом необходимо проверить статистическую значимость индекса детерминации: проверяется нулевая гипотеза ![]() , используется
, используется ![]() .
.
Таблица №6
| Регрессионная статистика | ||
| R-квадрат | 0,000109693 | |
![]() .
.
Т.к. Значение детерминации R-квадрат имеет малое значение, которое менее 1%, то дальнейшее решение не имеет смысла, т.к. вероятность того что прогноз будет верным меньше 1%.
Задача №2
Используя данные, приведенные в таблице: построить линейное уравнение множественной регрессии;
1) оценить значимость параметров данного уравнения и построить доверительные интервалы для каждого из параметров, оценить значимость уравнения в целом, пояснить экономический смысл полученных результатов;
2) рассчитать линейные коэффициенты частной корреляции и коэффициент множественной детерминации, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними;
3) вычислить прогнозное значение y при уменьшении вектора x на 6 % от максимального уровня, оценить ошибку прогноза и построить доверительный интервал прогноза;
Таблица №5
| номер наблюдения, i | Накопления семьи, Y (y.e.) | Доход семьи, X1 (y.e.) | Расходы на питание, X 2 (y.e.) |
| 1 | 2 | 20 | 5 |
| 2 | 6 | 27 | 6 |
| 3 | 7 | 26 | 7 |
| 4 | 5 | 19 | 5 |
| 5 | 4 | 15 | 5 |
| 6 | 2 | 15 | 5 |
| 7 | 7 | 28 | 10 |
| 8 | 6 | 24 | 7 |
| 9 | 4 | 14 | 6 |
| 10 | 5 | 21 | 7 |
| 11 | 5 | 20 | 10 |
| 12 | 3 | 18 | 6 |
Таблица №6 Параметры (коэффициенты) уравнения регрессии
| Коэффициенты | |
| Y-пересечение | -1,767785782 |
| x1 | 0,232792618 |
| x2 | 0,24953991 |
Множественная регрессия широко используется в решении проблем спроса, доходности акций, изучении функции издержек производства, в макроэкономических расчетах и целого ряда других вопросов эконометрики. В настоящее время множественная регрессия - один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии - построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.
На основании этих данных запишем уравнение регрессии:
![]() .
.
Таблица №7 Регрессионная статистика
| R-квадрат | 0,663668925 |
| Нормированный R-квадрат | 0,588928686 |
! Параметр R-квадрат, представляет собой квадрат коэффициента корреляции rxy2 и называется коэффициентом детерминации. Величина данного коэффициента характеризует долю дисперсии зависимой переменной y, объясненную регрессией (объясняющей переменной x). Соответственно величина 1 - rxy2 характеризует долю дисперсии переменной y, вызванную влиянием всех остальных, неучтенных в эконометрической модели объясняющих переменных. Доля всех неучтенных в полученной эконометрической модели объясняющих переменных приблизительно составляет: 0,663668, или 66,3%.
Находим, что численное значение ![]() , а скорректированный (нормированный, исправленный) коэффициент детерминации равен
, а скорректированный (нормированный, исправленный) коэффициент детерминации равен ![]()
1) Для оценки качества уравнения регрессии в целом необходимо проверить статистическую значимость индекса детерминации ![]() : проверяется нулевая гипотеза
: проверяется нулевая гипотеза ![]() , используется
, используется ![]() .
.
Наблюдаемое значение критерия ![]() и оценку его значимости находим в Таблице №8
и оценку его значимости находим в Таблице №8
Таблица №8 Дисперсионный анализ:
| F | Значимость F |
| 8,87967358 | 0,007420813 |
! Включаемые в уравнение множественной регрессии факторы должны объяснить вариацию зависимой переменной. Если строится модель с некоторым набором факторов, то для нее рассчитывается показатель детерминации, который фиксирует долю объясненной вариации результативного признака (объясняемой переменной) за счет рассматриваемых в регрессии факторов. А оценка влияния других, неучтенных в модели факторов, оценивается вычитанием из единицы коэффициента детерминации, что и приводит к соответствующей остаточной дисперсии.
Таким образом, при дополнительном включении в регрессию еще одного фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться. Если этого не происходит и данные показатели практически недостаточно значимо отличаются друг от друга, то включаемый в анализ дополнительный фактор не улучшает модель и практически является лишним фактором.
Если модель насыщается такими лишними факторами, то не только не снижается величина остаточной дисперсии и не увеличивается показатель детерминации, но, более того, снижается статистическая значимость параметров регрессии по критерию Стьюдента вплоть до статистической незначимости.
2) Для статистической оценки значимости коэффициентов регрессии (![]() ) используем
) используем ![]() статистику Стьюдента.
статистику Стьюдента.
Проверяется нулевая гипотеза ![]() .
.
Для проверки нулевой гипотезы необходимо знать величину наблюдаемых значений критерия ![]() . Их значения и оценки их статистической значимости найдем в Таблице №9
. Их значения и оценки их статистической значимости найдем в Таблице №9
Таблица №9
| t-статистика | P-Значение |
| -1,127971079 | 0,28850322 |
| 2,838964459 | 0,01943598 |
| 1,130728736 | 0,28740002 |
В этой же таблице находим границы доверительных интервалов для каждого из параметров:
| Нижние 95% | Верхние 95% |
| -5,313097658 | 1,777526094 |
| 0,047297697 | 0,418287538 |
| -0,249694323 | 0,748774142 |
Похожие работы
... и детерминации и F-критериев Фишера наибольшие. 3. Множественная регрессия Цель работы – овладеть методикой построения линейных моделей множественной регрессии, оценки их существенности и значимости, расчетом показателей множественной регрессии и корреляции. Постановка задачи. По данным изучаемых регионов (таблица 1) изучить зависимость общего коэффициента рождаемости () от уровня бедности ...
... и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0: . Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов. Проверка мультиколлинеарности факторов может быть ...
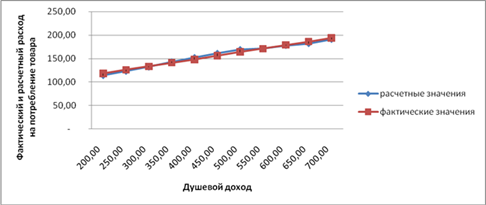
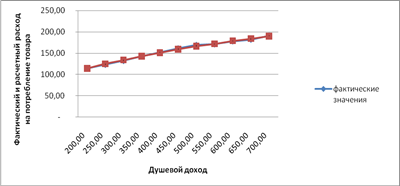
трех исследованных моделей. Отбор факторов и показателей для построения функции потребления Исходные данные, характеризующие изменение душевого дохода (Х) и расхода на потребление товара А (Y) приведены в таблице 1. Таблица 1 - Исходные данные Душевой доход (X) (ден. ед) Расход на потребление товара А (Y) (ден. ед) X² X*Y Y² 200,00 114,00 40 000 ...
... взяты за 2003 год. Данные взяты из статистического сборника Регионы России Социально-экономические показатели. 2003. Федеральная служба государственной статистики Построение модели множественной регрессии Расчет параметров Рассчитаем необходимые параметры: Признак Ср. знач. СКО Характеристики тесноты связи βi bi Коэф-ты частной корр. F-критерий фактический ...
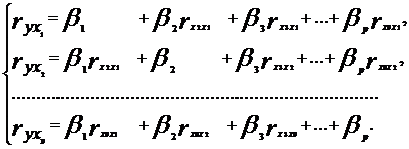
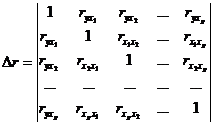
0 комментариев