Навигация
Методика построения уравнения регрессии и корреляции
Контрольная работа №2
Задача №1
Для изучения связи между активами-нетто и объемом капитала по 30 коммерческим банкам (согласно Вашему варианту):
а) изобразите связь между изучаемыми признаками графически построением поля корреляции;
б) постройте уравнение регрессии. Параметры уравнения определите методом наименьших квадратов. Рассчитайте теоретические значения объема кредитных вложений и нанесите их на построенный график.
Решение:
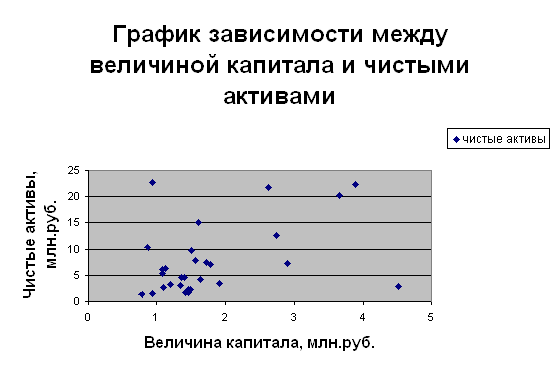
Рисунок 1
Расчетная таблица для определения параметров уравнения регрессии зависимости чистых активов и капитала коммерческих банков.
Таблица 1.1
| № банка | Капитал, млн.руб. (X) | Чистые активы, млн.руб. (Y) | X² | Y² | X*Y | Yx |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 1,46 | 1,68 | 2,13 | 2,82 | 2,45 | 232,1 |
| 2 | 1,51 | 2,81 | 2,28 | 7,9 | 4,24 | 240,4 |
| 3 | 2,63 | 21,84 | 6,92 | 476,9 | 57,44 | 422,0 |
| 4 | 1,72 | 7,38 | 2,96 | 54,46 | 12,7 | 264,8 |
| 5 | 1,50 | 9,82 | 2,25 | 96,43 | 14,73 | 240,1 |
| 6 | 1,64 | 4,26 | 2,69 | 18,15 | 6,99 | 258,2 |
| 7 | 1,36 | 4,61 | 1,85 | 21,25 | 6,27 | 228,4 |
| 8 | 1,21 | 3,32 | 1,46 | 11,02 | 4,02 | 219,6 |
| 9 | 1,49 | 2,33 | 2,22 | 5,43 | 3,47 | 234,9 |
| 10 | 1,35 | 3,08 | 1,82 | 9,49 | 4,16 | 227,6 |
| 11 | 1,61 | 15,14 | 2,59 | 229,2 | 24,37 | 254,8 |
| 12 | 1,78 | 7,12 | 3,17 | 50,7 | 12,67 | 266,1 |
| 13 | 1,42 | 1,68 | 2,01 | 2,82 | 2,38 | 229,7 |
| 14 | 1,41 | 4,60 | 1,99 | 21,16 | 6,49 | 229,2 |
| 15 | 1,46 | 2,20 | 2,13 | 4,84 | 3,21 | 232,1 |
| 16 | 3,65 | 20,21 | 13,32 | 408,4 | 73,77 | 587,4 |
| 17 | 1,57 | 7,74 | 2,46 | 59,9 | 12,15 | 252,1 |
| 18 | 1,10 | 2,72 | 1,21 | 7,4 | 2,99 | 173,8 |
| 19 | 0,94 | 1,59 | 0,88 | 2,53 | 1,49 | 151,9 |
| 20 | 3,89 | 22,37 | 15,13 | 500,42 | 87,02 | 598,4 |
| 21 | 0,78 | 1,42 | 0,61 | 2,02 | 1,11 | 121,9 |
| 22 | 2,74 | 12,61 | 7,51 | 159,01 | 34,55 | 439,8 |
| 23 | 0,87 | 10,26 | 0,76 | 105,27 | 8,93 | 136,6 |
| 24 | 1,08 | 6,12 | 1,17 | 37,45 | 6,61 | 169,9 |
| 25 | 1,08 | 5,27 | 1,17 | 27,8 | 5,69 | 169,9 |
| 26 | 2,90 | 7,33 | 8,41 | 53,73 | 21,26 | 465,8 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 27 | 1,13 | 6,30 | 1,28 | 39,69 | 7,12 | 178,7 |
| 28 | 0.94 | 22,67 | 0,88 | 513,93 | 21,31 | 151,9 |
| 29 | 1.92 | 3,42 | 3,69 | 11,7 | 6,57 | 306,8 |
| ИТОГО | 48,14 | 221,9 | 96,95 | 2941,81 | 456,16 | 7684,9 |
Система нормальных уравнений для нахождения параметров парной регрессии методом наименьших квадратов имеет следующий вид:
![]()
а0 = (221,9 – 48,14а1)/29
48,14*((221,9 – 48,14а1)/29)+ 96,95а1 = 456,16
368,354 – 79,912а1 + 96,95а1 = 456,16
17,037а1 = 87,806
а1 = 5,154
а0 = (221,9 – 48,14*5,154)/29 = -0,9
Yx = а0 + а1*х = 5,154х - 0,9
Задача №2
По данным задачи 1 вычислите показатели тесноты связи между изучаемыми признаками. В случае линейной связи для оценки тесноты связи необходимо применить формулу линейного коэффициента корреляции, при нелинейной связи – теоретического корреляционного отношения.
Сделайте выводы о тесноте и направлении связи между изучаемыми признаками.
Решение
Линейный коэффициент корреляции рассчитывается по формуле:
![]()
σх = √х² - (х)²
σу = √у² - (у)²
х² = ∑ х²/29 = 96,95/29 = 3,34
(х)² = (∑ х/29)² = (48,14/29)² = 2,756
у² = ∑ у²/29 = 2941,81/29 = 101,441
(у)² = (∑ у/29)² = (221,9/29) ² = 58,549
X = ∑ х/29 = 48,14/29 = 1,66
Y = ∑ у/29 = 221,9/29 = 7,65
XY = ∑х*у/29 = 456,16/29 = 15,73
σх =√3,34 – 2,756 = 0,764
σу = √101,441 – 58,549 = 6,55
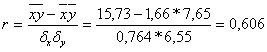
Задача №3
По данным любого статистического ежегодника или периодической печати выполните следующее:
1. Выберите интервальный ряд динамики, состоящий из 8-10 уровней.
2. Изобразите графически динамику ряда с помощью статистической кривой.
3. По данным выбранного ряда вычислите абсолютные и относительные показатели динамики. Результаты расчетов изложите в табличной форме.
4. Вычислите средние показатели динамики.
Решение
1. Выберем интервальный ряд динамики, состоящий из восьми уровней и отразим его в таблице 3.1
Таблица 3.1. Среднемесячное потребление горячей воды в течение 8-ми месяцев, куб.м.
| Месяц | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| куб.м. | 10,5 | 9,8 | 7,4 | 9,6 | 10,9 | 9,2 | 13,7 | 11,3 |
Рассмотрим динамический ряд потребления горячей воды в таблице 3.2
Таблица 3.2. Динамика потребления горячей воды за 8 месяцев
| Месяц | Потребление, куб.м.(уi) | Абсолютные приросты, куб.м. | Темпы роста, % | Темпы прироста, % | Абсолютное значение 1% прироста, куб.м. | |||
| цепные | базисные | цепные | базисные | цепные | базисные | |||
| 1 | 10,5 | - | - | - | 100 | - | - | - |
| 2 | 9,8 | -0,7 | -0,7 | 93,3 | 93,3 | -6,7 | -6,7 | 0,105 |
| 3 | 7,4 | -2,4 | -3,1 | 75,5 | 70,5 | -24,5 | -29,5 | 0,098 |
| 4 | 9,6 | 2,2 | -0,9 | 129,7 | 91,4 | 29,7 | -8,6 | 0,074 |
| 5 | 10,9 | 1,3 | 0,4 | 113,5 | 103,8 | 13,5 | 3,8 | 0,096 |
| 6 | 9,2 | -1,7 | -1,3 | 84,4 | 87,6 | -15,6 | -12,4 | 0,109 |
| 7 | 13,7 | 4,5 | 3,2 | 148,9 | 130,5 | 48,9 | 30,5 | 0,092 |
| 8 | 11,3 | -2,4 | 0,8 | 82,5 | 107,6 | -17,5 | 7,6 | 0,137 |
| Итого | 82,4 | 0,8 | - | - | - | - | - | - |
Похожие работы
... и детерминации и F-критериев Фишера наибольшие. 3. Множественная регрессия Цель работы – овладеть методикой построения линейных моделей множественной регрессии, оценки их существенности и значимости, расчетом показателей множественной регрессии и корреляции. Постановка задачи. По данным изучаемых регионов (таблица 1) изучить зависимость общего коэффициента рождаемости () от уровня бедности ...
... t-критерий Стъюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Но о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки: Оценка значимости коэффициентов чистой регрессии с помощью /-критерия ...
... на трудовые коллективы. Выводы и предложения В ходе выполнения данного курсового проекта был проведен статистико-экономический анализ производства подсолнечника в СХА "Заря" и других хозяйствах Павловского, Петропавловского, Воробьевского и Аннинского районов Воронежской области. Воспользовавшись методикой анализа рядов динамики, мы увидели, что средние показатели ряда динамики ...
... выработки, не включаемых в стоимость продукции, и добавить прирост или вычесть уменьшение остатка по счету «Резерв предстоящих расходов и платежей». [23, с. 186] 1.2 Динамики производственных затрат на производство зерна, сахарной свеклы, подсолнечника за 6 лет Произведем анализ динамики производственных затрат зерна, сахарной свеклы и подсолнечника за 6 лет. Исходные данные приведены в ...
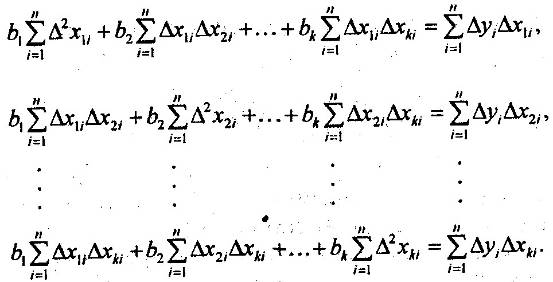

0 комментариев