Ряды динамики, к-рые хар-ют изменение эк-ких явлений во времени

2. Ряды динамики, к-рые хар-ют изменение эк-ких явлений во времени.

Статистические таблицы

Стат таблицы – это форма систематизированного, рационального и наглядного изложения результатов сводки и обработки стат материалов.

Стат таблицы облегчают наглядное чтение, усвоение стат материалов. В любой стат таблице различают подлежащее и сказуемое.

Подлежащее – это объекты или их группы, данные к-рых содержатся в таблице.

По своему содержанию подл подразделяется на 3 вида: простые, груп-вые, комбин-ные. Простой наз таблицу, подлежащее к-рой содер-тся наименование объекта.

Групповой наз таблицу, подлежащее к-рой образовано груп объектов.

Комбинированные – таблицы, в подлежащем к-рой содерж по 2 и более признакам комбинации.

Сказуемое – это перечень показателей, к-рыми хар-ся подлежащее. Это то, что говорится о подлежащем, но в цифровом значение. Сказ подраз на виды таблиц. Простые. При простой разработке показатели, к-рые его образуют, располагаются параллельно. При сложной груп показатели располагаются в соотв сочетаниях между собой.

Абсолютные величины

- показатели, к-рые выражают общ-ные явления и процессы числом единиц совокупности. Получаются величины в результате сводки стат материала или расчетным путем. Абсол величины хар-ют: численность сов-сти, объем изучаемого признака, уровень явлений на опред момент, результаты процессов за опред период времени.

Абсол величины подразделяются на индивидуальные – это размер кол-ных признаков у отдельных единиц изучаемой совокупности (S посевной). Инд величины – в результате стат набл. и общие - величины, к-рые выражают размер колич признаков у всех единиц изучаемой совокупности. Данные вел получают расчетным путем и показывают наличие и движение матер, фин-вых и трудовых ресурсов. Общие вел служат базой плановых расчетов проверки выполнения планов и т.д.

Абсол величины всегда выражаются в именованных числах и в опред единицах измерения (м, шт, т, грн). Все эти единицы измерения могут быть натур, условно-натур, трудовыми и денежными. Натуральные: простые, комбинированные, комплексные. Условно-натуральные показатели применяются при исчислении продукции консервных заводов в тубах т.е. в тыс усл банках. Т.к. простой расчет в тыс шт не дает правильного представления об объеме пр-ва, поскольку консерв заводы выпускают продукцию в различных по емкости банках, то за усл единицу принята банка 353, 4 см³. за у. е. мощности применяется 15-ти сильный трактор. За у. е. 1 т топлива применяется коэф перевода угля 0,9 т, природ газа 1,2 т. пр-во мыла в усл 40% мыле.

Сущность относ величин

 

- показатели, выражающие кол-ные соотношения численности или величины признаков изучаемых явлений. Данные вел-ны получ-тся в резул. сравнен. 2 показателей.

Тот показатель, к-рый сравнивается наз отчетной величиной, отражается в числителе дроби. Та величина, с к-рой сравнивают наз основанием или же базой сравнения, располагается в знаменателе дроби. Если основ принять за 1, то относ вел выразится в форме коэф и покажет во сколько раз сравниваемая величина больше или меньше отчетной. Относит вел зависят от хар-ра данных и результатов, к-рые получаются при сопоставлении кол-ных соотношений, кол-ные соизмерения подразделяются на виды.

1. ОВВП. Имеет самое распрост применение в стат. 2. ОВПЗ получается в результате сравнения планов буд периода с факт уровнем отчетного периода, принятого за базу. 3. ОВД хар-ет темп общ-ного развития. 4. ОВС хар-ет состав изучаемой сов-сти, а также показывает строение совок-сти. 5. ОВСр отражает соотношение 2-х объемов или уровней пространства. 6. ОВК получается посредством деления друг на друга разноименных исходных показателей. Она дает типичную хар-ку соотношения однопорядковых по значению исходных показателей. 7. ОВИ представляет собой отношение величины явления, обладающим каким-либо опред признаком к размеру среды, к-рая его породила или развивается.

Хар-ка сред величин

Наз показатели, к-рые выражают типичные черты и дают обобщающий показатель, варьирующего признака по совокупности однор явлений. Сред вел выражают качест сторону изучаемых процессов. Для опред сред величин необходимо правильно выбрать формулу сред величины. Исходной базой или критерием выбранной формы явл соотношение, к-рое выражает смысл сред величины и ее зависимость от др показателей. Сред вел могут вычислятся как для совок-сти в целом и их наз общими средними, так и для отдел групп и их наз групповыми или частными средними.

Общее сред может быть вычислено как сред из групповых средних и взвешенное по объектам групп. Сред величины должны вычислятьсяс учетом опред показателя, к-рый имеет только ему присущее содержание.

1. сренеарифмет. 2. среднегармоническое по своей форме явл величиной обратной среднеарифметической. Среднегарм фор-лу применяют тогда, когда в исходных данных частот и вариант незаданных обходят как сомножитель в один из изменяющихся показателей. 3. среднегеометрическое применяется при расчете сред темпов изменения явления во времени. 4. Среднехронологическое применяется для определения среднегодовой численности населения, остатков оборотных ср-в, среднегод числа рабочих и служащих, в с/х для среднегодовой численности скота. 5. среднеквадратическое применяется в тех случаях, когда в исходной инф-ции усредняемые величины представлены линейными мерами. Формула необходима для расчета средних диаметров труб, стволов деревьев.

Мода и медиана

Для хар-ки структуры варяц рядов применяются показатели, к-рые наз структурные средние. К ним относятся мода и медиана.

Мода – это наиболее часто встречающаяся величина признак в данной совокупности.

Медиана – это значение изменяющегося признака, к-рое находится в середине варяц. Ряда и все варианты вокруг него расположены в порядке возрастания или убывания значений признака.

В дискр ряду для опред медианы необходимо сумму частот разделить пополам и к полученному результату добавить ½.

Сущность вариации

При изучении явлений нельзя ограничиваться только средними величинами и их признаками. Необходимо подвергать эти явления всестороннему анализу отклонения от средних т.к. без этого отклонения невозможно увидеть процесс развития явления. При исчил. средне арифметических необходимо рассматривать как отдельные значения изучаемого признака группируются вокруг средней, в той мере, в какой они сосредоточены вокруг нее и близко или далеко располагаются от этой средней. В одних случаях отдельные значения признака могут находится близко к сред. арифметической и мало чем отлич. от нее. В этих усл. среднее представл. всю сов-ть. В др.случаях отдельные значения далеко расположены от средней. В в таких усл.средняя будет представлять вся сов-ть.

Нельзя ограничиваться одной сред.величеной, нужны еще показатели, к-рые хар-ли бы отклонения отдельных значений о общей средней. Также необходимо изучать соотношение сред. арифметических данного признак с распределением по данному признаку. Вариация – колеблемость признака около средней величины.

Показатели вариации

В статистике применяются следующие показатели вариации:

1.Размах вариации – разность между max и min размахом вариации. Этот показатель имеет недостаток, к-рый заключ. в том, что он зависит от отдельных случаев, к-рые не всегда достаточно хар-ны. И если на них опираться то результату будут не верные.

2.Среднее линейное отклонение(d) – представл. собой сред. величину значения признака от их средней величины. Данный показатель широко применяется на практике с его помощью анализируется состав работающих, равномерность поставок, разрабатывается система стимулирования работников. Но этот показатель усложняет расчеты вероятности, затрудняет использование мат-кой статистики. Поэтому для измерения вариаций используют дисперсию.

3.Дисперсия(G). Если сов-ть разбита на части или группы по изучаемому признаку, то для данной сов-ти можно применить расчеты след. видов дисперсии: 1.групповая(частная) – равна сред. квадрату отклонений отдельных значений признака внутри группы от сред. арифметической этой группы. 2.сред.из групповых – сред. арифметическая взвешенная из групповых. 3.межгрупповая – средняя варианта отклонений. Она хар-ет вариацию результативного признака. Между видами дисперсии сущ.определенное соотношение. Общая дисперсия равна сумме межгрупповой и сред. из групповых.

4.Сред.квадратическое отклонение (простое, взвешенное)

5.Коэффициент вариации, в отличие от сред. линейного и сред. квадратического отклонения коэф. вариации(V) явл.мерой относительной колеблемости признака около средней величины и хар-ет степень однородности признака в изуч.сов-ти.

Понятие о статистических рядах динамики

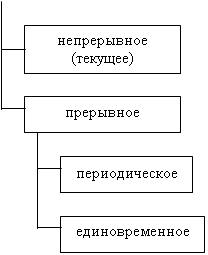
Ряды динамики – ряд стаистич. чисел, к-рые хар-ся изменением величины общ-ного явления во времени. В каждом ряде динамики имеется 2 осн. элемента: 1.показатель времени – может опред. как на определенный момент времени, так и на отдельные периоды. 2. уровни ряда динамики, к-рые отраж. количественную оценку развития во времени изуч. явления. Данные уровни могут быть выражены в абсолютных, относительных средних величинах. В рядах динамики уровни имеют след.значение: начальные; конечные; средние. В зависимости от хар-ра изуч.явления уровни ряда динамики могут относиться к определенным датам или же отдельным периодам. В связи с этим их делят на 2 вида:

1.Моментный – ряд динамики, уровни к-рого хар-ют размеры общ-ного явления по состоянию на определенный момент. Особенностью моментного ряда явл. то, что в его уровни могут входить одни и те же единицы сов-ти. с помощью моментного ряда изуч. объем валовой продукции, расходы сырья, кол-во оборудования ит.д. В моментных рядах сред. уровни исчисляются след. способами: 1. применяется в том случае если моментный ряд динамики имеет равные промежутки времени между двумя датами. 2. применяется в том случае если моментный ряд динамики имеет неодинаковые промежутки времени между двумя датами.

2.Периодиеский – ряд динамики уровни, к-рого хар-ют размеры общ-ного явления за опред. периоды времени. Особенностью данного ряда явл. то, что каждый его уровень складывается из данных за более короткие интервалы времени.

Статистическое отражение развития изуч. явления во времени может быть представлено рядами динамики с нарастающим итогом. Их применяют для отображения результатов развития изучаемых показателей не только за отчетный период, но и с учетом предшествующих периодов. При составлении таких рядов осущ. последовательное суммирование смежных уровней, этим достигается суммарное обобщение результатов развития изучаемого показателя с начала отчетного периода.

Сопоставимость в рядах динамики

Сопоставимость данных – соответствие условий и методов расчета ее показателей, обеспечивающих правильность получаемых при их сравнении выводов о различии между изуч. явлениями. К сопоставимости динамического ряда предъявляются следующие требования:1.все показатели ряда динамики должны быть достоверными и научно обоснованными.2.интервалы времени должны быть сходны в эк-ком отношении.3.должны быть единые единицы измерения.4.показатели ряда динамики должны быть сопоставимы по составу.5.уровни ряда динамики должны иметь единые способы ичисления.6. показатели ряда динамики должны быть сопоставимы по тер-рии, к к-рой они относятся.

Для выявления тенденции развития эк-кого явл в динамике применяются след. методы: 1.метод укрупнения периода- уровни исходного динамического ряда объединяются по более крупным периодам. 2. метод скользящей средней – суть в замене первоначальных уровней динамики сред. арифметическими, найденных по способу скольжения начиная с первого уровня с включением последующих уровней, т.е. при расчете каждого последующего сглаженного уровня принятый для укрупнения период сдвигается на одну дату. 3.метод аналитического выравнивания – суть в том, что подбирается уравнение , к-рое отраж.хар-р изменения динамического ряда за изуч.период.

Показатели рядов динамики

В статистике для того, что бы выявить особенности развития изуч. явл. и процессов за опред. периоды времени исчисляются абсолютные и относительные показатели ряда динамики. К ним относятся:

1.абсолютный прирост – разность между уровнями данного периода и периода принятого за базу сравнения

2. абсолютное значение 1% прироста –хар-ет эквивалент 1% прироста

3.темп роста – хар-ет сред. относительный рост явл. за изучаемый период

4. темп прироста – хар-ет относительный прирост явления в отчетном периоде по сравнению с тем уровнем, с к-рым осущ.сравнение.

5. средний темп роста

6 средний темп прироста

В основе расчета показателей ряда динамики лежит сравнение уровней. В зависимости от применяемого способа сопоставления показатели динамики могут вычисляться на постоянной и переменной базах. Для расчета показателей на постоянной базе каждый уровень сравнивается с одним и тем же показателем и наз.базисным. для расчетов показателей на переменной базе последующий уровень сравнивается с предыдущим и наз.цепным.

Понятие о выборочном наблюдении

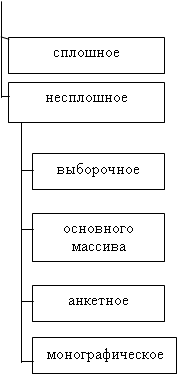
Выборочное наблюдение – не сплошное наблюдение, при к-ром отбор единиц сов-ти осущ. случайно. При выборочном наблюдении отобранная часть подвергается обследованию, после чего получ. результаты распространяемые на всю исходную сов-ть. К применению данного метода прибегают в следующих случаях:

1.когда само наблюдение связано с порчей или уничтожением наблюдаемых единиц