Статистичне вивчення фінансово-господарських результатів діяльності, продуктивність праці та оплати праці в ВАТ "Дніпропетровський завод металоконструкцій ім. Бабушкіна"

КУРСОВИЙ ПРОЕКТ

З ДИСЦИПЛІНИ „СТАТИСТИКА”

на тему „ СТАТИСТИЧНЕ ВИВЧЕННЯ ФІНАНСОВО-ГОСПОДАРСЬКИХ РЕЗУЛЬТАТІВ ДІЯЛЬНОСТІ, ПРОДУКТИВНІСТЬ ПРАЦІ ТА ОПЛАТИ ПРАЦІ В ВАТ "ДНIПРОПЕТРОВСЬКИЙ ЗАВОД МЕТАЛОКОНСТРУКЦIЙ IМ. БАБУШКIНА"”

КИЇВ

2006

ВСТУП

Статистика – це наука, яка вивчає розміри і кількісні співвідношення масових суспільно-економічних явищ і процесів у нерозривному зв ' язку з їх якісним змістом.

Для вивчення кількісного аспекту масових суспільно-економічних явищ і процесів статистика використовує ряд понять і категорій: 1)ознака; 2)варіація;

3) статистична сукупність; 4)показник; 5) система показників.

Ознакою в статистиці називають відмінну рису, властивість, якість, що є характерною для окремих одиниць. об ' єктів(явищ). Статистична сукупність – це велика кількість одиниць, об ' єктів, явищ, об ' єднаних будь-якими загальними властивостями(ознаками), що піддаються статистичному вивченню.

Під статистичним показником розуміють узагальнену кількісну характеристику соціально-економічних явищ і процесів у їх якісній визначеності щодо конкретних умов місця і часу.

Систематизація та підсумовування даних з метою одержання узагальненої характеристики досліджуваного явища за рядом істотних ознак називають статистичним зведенням.

Групування – це процес утворення однорідних груп на основі розподілу всієї сукупності досліджуваного явища на окремі групи(частини) за найбільш істотними ознаками.

Все розмаїття ознак, на основі яких можуть здійснюватися статистичні групування, можна класифікувати наступним чином:

1) за формою вираження – на атрибутивні та кількісні(варіаційні);

2) за характером коливності – на альтернативні та варіаційні;

3) за роллю, яку вони відіграють в процесі – на факторні та результативні.

У ході аналізу параметрів діяльності підприємства для характеристики різних аспектів фінансового стану застосовуються як абсолютні показники, так і фінансові коефіцієнти, що представляють собою відносні показники фінансового стану. Останні розраховуються у виді відносин абсолютних показників фінансового стану чи їхніх лінійних комбінацій. Відповідно до класифікації, відносні показники фінансового стану підрозділяються на коефіцієнти розподілу і коефіцієнти координації.

Коефіцієнти розподілу застосовуються в тих випадках, коли потрібно визначити, яку частину той чи інший абсолютний показник фінансового стану складає від підсумку його групи абсолютних показників. Коефіцієнти розподілу і їхньої зміни за звітний період, як буде показано нижче, відіграють велику роль у ході попереднього ознайомлення з фінансовим станом по порівняльному аналітичному нетто.

Коефіцієнти координації використовуються для вираження відносин різних власне кажучи абсолютних показників фінансового стану чи їхніх лінійних комбінацій, що мають різний особистий економічний зміст.

Аналіз фінансових коефіцієнтів полягає в порівнянні їхнього значення з базисними величинами, а також у вивченні їхньої динаміки за звітний період і за ряд років. Як базисні величини використовуються усереднені по хронологічному ряду значення показників даного підприємства, що відносяться до минулих сприятливих з погляду фінансового стану періодів чи середньогалузевих значень показників.

Цілями курсового проекту було – статистична оцінка динаміки абсолютних показників та структури доходів підприємства, динаміки рівней продуктивності праці та структурної частини заробітної плати в витратах підприємства.

В курсовій роботі проведений статистичний аналіз характеристик балансів та декларацій по формуванню податку на прибуток ВАТ"ДНIПРОПЕТРОВСЬ-КИЙ ЗАВОД МЕТАЛОКОНСТРУКЦIЙ IМ.БАБУШКIНА" за 2004 -2005 роки.

РОЗДІЛ 1. СТАТИСТИЧНІ ДОСЛІДЖЕННЯ ФІНАНСОВО-ЕКОНОМІЧНИХ ХАРАКТЕРИСТИК ДІЯЛЬНОСТІ ПІДПРИЄМСТВА

1.1 Статистичні спостереження

 

Закономірність – це повторюваність, послідовність та порядок у розвитку соціальних явищ. Вона може проявлятися по-різному. В філософії розрізняють два види закономірностей: динамічну та статистичну.

Динамічна закономірність – це така, яка виявляється в кожному окремому випадку і не злежить від кількості одиниць, які ми спостерігаємо. Вона притаманна природним явищам. Наприклад, закон Архімеда можна виявити і н одному об’єкті, який занурюють в рідину, і на тисячі об’єктів. Аналогічним чином можна виявити закон земного тяжіння та інші фізичні, хімічні та математичні закони.

Статистична закономірність – це така, яка виявляється лише в достатній кількості однорідних одиничних елементів, котрі й утворюють сукупність. Тобто кожний окремий елемент може не підтверджувати існування тієї чи іншої закономірності, тому що існування її в кожному окремому елементі носить імовірний характер. Інакше кажучи, статистична закономірність властива лише сукупності одиниць, яка має назву статистичної сукупності.

Статистичні закономірності проявляються по-різному. Це можуть бути закономірності: 1) розвитку (динаміки) явищ (статистика свідчить про збільшення чисельності населення, зростання тривалості життя, зменшення середнього віку обрання шлюбу); 2) структурних зрушень (збільшення частки міського населення в загальній його чисельності, а також частки населення похилого віку в сільській місцевості); 3) розподілу елементів сукупності (розподіл населення за віком, сімей за числом дітей, середньодушовим доходом); 4) зв’язку між явищами (залежність продуктивності праці від фондоозброєності, собівартості продукції від продуктивності праці).

Статистична сукупність – це певна множина елементів, поєднаних однаковими умовами існування та розвитку. Об’єктивною основою існування статистичної сукупності є складне перетинання причин та умов, які формують той чи інший масовий процес, наприклад, зміни тенденції в розвитку злочинності від зміни соціально-економічної та політичної ситуації в країні.

Кожний окремий елемент, який складає статистичну сукупність, має назву одиниці сукупності. Кожна окрема одиниця сукупності є носієм явища, що вивчається, і відрізняється від іншої одиниці сукупності розміром ознаки. Завжди має місце коливання (варіювання) значень ознаки у кожній одиниці статистичної сукупності.

Явищами хімії, фізики, математики та інших природничих наук властиві лише динамічні закономірності.

Явища суспільного життя, які вивчаються статистикою, відносяться до статистичних закономірностей. Окремі елементи статистичної сукупності характеризуються значною кількістю різних ознак, але відповідно до мети дослідження вони мають загальні властивості, що і робить їх статистичною сукупністю. Ознака, яка приймає в межах сукупності різні значення, назива-ється варіюючою, а відмінність, коливання значень ознаки – варіацією. Склад елементів і спосіб об’єднання їх визначають структуру сукупності.

Ознаки поділяються на кількісні і атрибутивні (словесні). Якщо кількісна ознака представлена числом (стаж роботи, заробітна плата), то застосовують загально визнані еталони і одиниці виміру. Для атрибутивних ознак вимірювання означає реєстрацію наявності чи відсутності властивості, що вивчається (категорійні підрахунки).

Набір властивостей явища і відповідних їм чисел називають шкалою вимірювання. Теоретично існує багато типів шкал. За рівнем вимірювання і допустимими арифметичними діями виділяють метричну, номінальну, порядкову (рангову) шкали.

Метрична – це звичайна числова шкала обчислення, яку використовують для вимірювання фізичних величин ваги, довжини, часу) або результатів обчислення (прибуток, середня заробітна плата). Ознаки метричної шкали поділяються на дискретні і неперервні. Дискретні мають лише окремі, ізольовані значення. Неперервні ознаки мають будь-які значення в певних межах. Така визначеність неперервної ознаки дещо умовна, її завжди можна представити дискретною.

Номінальна – це шкала найменувань. “Оцифровка” ознак цієї шкали проводиться таким чином, щоб подібним елементам відповідало одне й те саме число, а неподібним – різні числа.

Порядкова (рангова) шкала встановлює не тільки відношення подібності елементів, а й послідовності – порядку. Це відношення типу “більше, ніж”, “краще, ніж” тощо. Кожному пункту шкали приписується число – ранг, число балів або будь-яка монотонно зростаюча функція (-2, -1, 0, 1, 2), що відбиває послідовність значень, але не відстань між ними.

Зібрані внаслідок статистичного спостереження первинні матеріали за допомогою зведення і групування узагальнюються, в результаті чого одержують зведені статистичні таблиці, в яких сукупності одиниць подаються в цілому та в розрізі груп[10].

Серед показників, які розраховуються в практиці статистичної роботи, можна виділити три групи за явними ознаками:

1) за суттю досліджуваних явищ розрізняють показники об ' ємні, що характеризують розміри явищ, процесів, та якісні, що характеризують кількісні співвідношення,характерні властивості досліджуваних явищ;

2) за ступенем агрегування явищ можна виділити індивідуальні, що виражають ознаки окремих одиниць сукупності, і загальні(узагальнюючі), що виражають розміри ознаки окремих груп або всієї сукупності;

3) залежно від характеру досліджувальних явищ розрізняють статистичні показники інтервальні, які ивражають розміри кількісної ознаки за певні періоди часу, і моментні, що виражають розміри кількісної ознаки на певний момент;

Абсолютні величини – це показники, які виражають розміри суспільно-економічних явищ і процесів в кокретних умовах часу і місця.

Відносними статистичними величинами називаються показники, які виражають кількісні співвідношення між явищами суспільно-економічного життя. Відносними величинами динаміки називаються показники, які виражають ступінь зміни явищ у часі.

Відносні величини структури характеризують склад досліджувальної сукупності. Зіставляючи струкутру однієї і тої ж сукупності за різні періоди часу, можна простежити за структурними змінами.

Однією з кількісних характеристик статистичних закономірностей є середня величина, яка здатна відобразити характерний рівень ознаки, притаманої усім елементам сукупності. Варіація будь-якої ознаки формується під впливом двох груп причин – основних, визначальних, які тісно пов’язані з природою самого явища, і другорядних, випадкових для сукупності в цілому.

Характерний, типовий рівень ознаки формується під впливом першої групи причин. Відхилення індивідуальних значень ознаки від типового зумовлені дією другорядних причин, які урівноважуються і тому на рівень середньої істотно не впливають. Середня характеризує типовий рівень варіаційної ознаки. Вона відображує в собі те спільне, характерне, що об’єднує всю масу елементів, тобто статистичну сукупність. Проте слід пам’ятати, що середня відображає типовий рівень ознаки лише в тому випадку, коли статистична сукупність, за якою вона обчислюється, якісно однорідна. Це одна з основних умов наукового застосування середніх у статистиці. Крім того, типовий рівень ознаки, що вивчається, проявляє себе лише у випадку узагальнення масових фактів. В цьому проявляється дія закону великих чисел [9].

За допомогою середніх величин масу елементів можна охарактеризувати одним числом, не зважаючи на те, що середня величина абстрактна і може не збігатися з жодним з індивідуальних значень ознаки. Вона відображає те загальне, типове для маси явищ, яке реально існує в конкретних умовах простору і часу. За допомогою середніх можна здійснити порівняльний аналіз кількох сукупностей, дати характеристику закономірностей розвитку соціально-економічних явищ і процесів. Не слід змішувати середні з відносними величинами інтенсивності. Середня завжди узагальнює кількісну варіацію ознаки, яка тією чи іншою мірою властива всім без винятку елементам сукупності.

Статистична середня – одна з найважливіших кількісно-якісних категорій, яку широко використовують у планово-аналітичній роботі підприємств і організацій. Поширення набуло обчислення таких показників, як середня врожайність, середня заробітна плата, середній рівень продуктивності праці та інше.

При вивченні закономірностей розподілу застосовують середню арифметичну, варіації – середня квадратичну, інтенсивності розвитку – середню геометричну. Вибір середньої має ґрунтуватися на всебічному теоретичному аналізі суті явищ та наявній інформації. Середня лише тоді може бути справжньою узагальнюючою характеристикою, коли при заміні нею всіх варіантів загальний обсяг варіаційної ознаки залишиться незмінним. Отже, залежно від того, що являє собою загальний обсяг варіаційної ознаки, в кожному конкретному випадку обирають вид середньої.

Варіація, тобто коливання, мінливість значень будь-якої ознаки є властивістю статистичної сукупності. Вона зумовлена дією безлічі взаємопов’язаних причин, серед яких є основні і другорядні. Основні причини формують центр розподілу, другорядні – його варіацію ознак, сукупна їх дія – форму розподілу.

Статистичні характеристики центру розподілу (середня, мода, медіана) відіграють важливу роль у вивченні статистичних сукупностей. В одних сукупностях індивідуальні значення ознаки значно відхиляються від центру розподілу, в інших – тісно групуються навколо нього, а відтак виникає потреба оцінити поряд з характеристиками центру розподілу міру і ступінь варіації. Чим менше варіація, тим однорідніша сукупність, отже, тим більш надійні і типові характеристики центру розподілу, насамперед середні величини.

Вивчення варіації має велике значення для оцінки сталості та диференціації соціально-економічних явищ, при використанні вибіркового та інших статистичних методів.

Середнє відбиває те загальне, що складається в кожному окремому, одиничному об'єкті завдяки цьому середня одержує велике значення для виявлення закономірностей властивим масовим суспільним явищам і непомітних в одиничних явищах. Середня відображає об'єктивну властивість явища. У дійсності часто існує тільки відхилені явища, і середня як явище може і не існувати, хоча поняття типовості явища і запозичається з дійсності.Індивідуальні значення досліджуваної ознаки в окремих одиницях сукупності можуть бути тими чи іншими (наприклад, ціни в окремих продавців). Ці значення неможливо пояснити, не просліджуючи причинно-наслідувальні зв'язки. Тому середня величина індивідуальних значень того самого виду є продукт необхідності. Він є результатом сукупної дії всієї єдиної сукупності, що виявляється в масі повторюваних випадків, опосередковуваних загальними умовами процесу[8].

Розподіл індивідуального значення досліджуваної ознаки породжує випадковість його відхилення від середніх, але не випадкове середнє відхилення, що дорівнює нулю.

Для кращого розуміння і аналізу досліджувальних статистичних даних, їх потрібно систематизувати, побудувавши хронологічні ряди, які називаються рядами динаміки або часовими рядами.

Розподіл індивідуального значення досліджуваної ознаки породжує випадковість його відхилення від середніх, але не випадкове середнє відхилення, що дорівнює нулю.

Середня, розрахована по сукупності в цілому називається загальною середньою, середні, обчислені для кожної групи - груповими середніми. Загальна середня відбиває загальні риси досліджуваного явища, групова середня дає характеристику розміру явища, що складається в конкретних умовах даної групи.

Визначальній функції відповідає рівняння середніх, знаючи визначальну функцію і рівняння середніх

 чи  (1.1)

одержуємо формулу [4]:

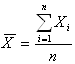 (1.2)

де Х_i - індивідуальне значення ознаки кожної одиниці сукупності;

n - число одиниць сукупності.

Здатність середніх величин зберігати властивості статистичних сукупностей називають визначальною властивістю.

Для кращого розуміння і аналізу досліджувальних статистичних даних, їх потрібно систематизувати, побудувавши хронологічні ряди, які називаються рядами динаміки або часовими рядами.

Кожний ряд динаміки складається з двох елементів:

1) періодів або моментів часу, до яких відносяться рівні ряду(t);

2) статистичних показників, які характеризують інтенсивності рівнів ряду(Y).

а)Характеристики статистичних вибірок

Для вимірювання та оцінки варіації використовують абсолютні та відносні характеристики. До абсолютних відносяться: варіаційний розмах, середнє лінійне та середнє квадратичне відхилення, дисперсія; відносні характеристики представлені низкою коефіцієнтів варіації.

Варіаційний розмах характеризує діапазон варіації, це різниця між максимальним і мінімальним значеннями ознаки:

 (1.3)

Узагальнюючою мірою варіації є середнє відхилення індивідуальних значень ознаки від центру розподілу.

Медіана вибірки – це значення, яке ділить розмах інтервалу вибірки на дві рівні частини.

Мода вибірки – це значення, яке найчастіше зустрічається в статистичному ряді вибірки.

Середня арифметична величина виборки розраховуэться як:

 (1.4)

Середнє лінійне відхилення:  (1.5)

Середнє квадратичне відхилення: 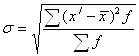 (1.6)

Середній квадрат відхилень – дисперсія: , (1.7)

де - середнє арифметичне інтервального ряду розподілу, f – частота.

Середнє лінійне та середнє квадратичне відхилення – іменовані числа (в одиницях вимірювання ознаки).

Порівнюючи варіації різних ознак або однієї ознаки у різних сукупностях, використовують відносні характеристики варіації. Коефіцієнти варіації розраховуються як відношення абсолютних, іменованих характеристик до центру розподілу і часто виражаються процентами:

Лінійний коефіцієнт варіації:  (1.8)

Квадратичний коефіцієнт варіації:  (1.9)

 

б) Динамічні ряди та їх характеристики

Динамічний ряд – це розміщені у хронологічній послідовності значення певного статистичного показника. складовими динамічного ряду є ознака часу (момент або інтервал) та числові значення показника – рівні.

Визначають абсолютні та відносні характеристики динаміки: абсолютний приріст та абсолютне значення 1% приросту; темп зростання та темп приросту. Розрахунок їх грунтується на порівнянні рівнів динамічного ряду. Якщо база порівняння постійна, характеристики динаміки називаються базисними, якщо база порівняння змінна – ланцюговими.

Абсолютний приріст (зменшення) – це різниця рівнів динамічного ряду:

базисні (1.10) ланцюгові  (1.11)

Сума ланцюгових абсолютних приростів дорівнює кінцевому базисному приросту

Темп зростання розраховується як відношення рівнів ряду, виражається коефіцієнтом або процентом:

базисні  (1.12)ланцюгові  (1.13)

Добуток ланцюгових темпів зростання дорівнює кінцевому базисному.

Темп приросту показує, на скільки процентів рівень більше рівня, взятого за базу порівняння. Його можна визначити як відношення абсолютного приросту до бази порівняння або безпосередньо на основі темпу зростання.

 (1.14) або  (1.15)

Абсолютне значення 1% приросту показує, чого вартий 1%; розраховується як співвідношення абсолютного приросту і темпу приросту:

 (1.16)

Узагальнюючими характеристиками інтенсивності динаміки є середній абсолютний приріст та середній темп зростання.

Середній абсолютний приріст розраховується як середня арифметична проста з ланцюгових абсолютних приростів:

, (1.17)

де n- число ланцюгових абсолютних приростів.

Середній темп зростання розраховується за формулою середньої геометричної:

 (1.18)

Середній темп приросту визначається як різниця між середнім темпом зростання одиницею (якщо середній темп зростання вигляді коефіцієнта), бо 100 (якщо він у процентах)

 (у вигляді коефіцієнтів); (1.19)

 (у вигляді процентів).

Середній темп приросту показує, на скільки процентів збільшився або зменшився рівень порівняно з попереднім в середньому за одиницю часу.

в ) Індексний аналіз статистичних вибірок

Індексом у статистиці називається відносний показник, який характеризує зміну рівня якогось суспільного явища з часом або його співвідношення у просторі. Прийнято розрізняти дві категорії індексів: індивідуальні та загальні. Індекс, який характеризує співвідношення величин окремого явища, називається індивідуальним, а індекс, котрий характеризує співвідношення рівнів усього явища в цілому або його частин, що складаються з кількох окремих елементів, які безпосередньо не піддаються підсумовуванню, - загальним.

Статистичний індекс – це узагальнюючий показник, який виражає співвідношення величин складного економічного явища, що складається з елементів безпосередньо несумірних. У статистиці розрізняють декілька ивдів індексів, в основу класифікації яких покладені різні ознаки [5]:

-  характер об ' єкта дослідження,

-  ступінь охоплення одиниць сукупності,

-  база порівняння,

-  вид зрівнюваних величин.

Індивідуальні індекси дають порівняльну характеристику окремих елементів складного явища і мають форму відношення певного показника у базисному (0) та звітному (1) періодах [5]:

 (1.20)

Загальний індекс є агрегатуваннням індивідуальних індексів і характеризує зміну сукупностей, до якої входять різнорідні елементи. Так загальна формула агрегатного індексу сукупності явищ у базисному (0) та звітному (1) періоді має наступний вираз(для вартісних економічних явищ, які характеризуються обсягами (q) та ціною (р) одиниці обсягу):

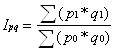 (1.21)

Для характеристики економічних явищ загальний агрегатний індекс (1.21) розбивають на два індекси:

-  загальний індекс фізичного обсягу вартісного явища (при умові незмінних цін р у базисному та звітному періодах):

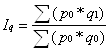 (1.22)

-  загальний індекс цін вартісного явища (при умові незмінного обсягу q у базисному та звітному періодах):

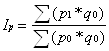 (1.23)

Для характеризування структурних зрушень середніх величин в вартісних економічних явищах застосовують індекси змінного складу, індекси постійного складу та індекси структурних зрушень, які формують систему взаємопов ' язаних індексів [5]:

-  для змінного індекса цін  (відношення середніх рівнів у базисному та звітному періодах):

 (1.24)

 (1.25)

де індекс цін постійного складу Ipz дорівнює:

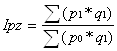 (1.26)

а індекс цін за рахунок структурних зрушень Id дорівнює:

 (1.27)

г) Регресійно –кореляційний аналіз динамічних рядів

Коефіцієнт кореляції між двома рядами вибірок X,Y величин розраховується за формулою [6]:

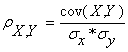 (1.28)

 - дисперсія вибірки величин Х; (1.29)

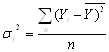 - дисперсія вибірки величин Y; (1.30)

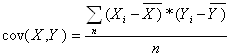 -коваріація виборок X,Y (1.31)

Для характеристики кореляційного зв’язку між факторною і результативною ознаками будується графік кореляційного поля та теоретична лінію регресії, визначаються параметри рівняння регресії.

Для перевірки істотності зв’язку потрібно порівняти фактичне значення статистики Фішера (F-критерій) з його критичним (табличним) значенням, яке потрібно визначити з урахуванням умов аналітичного групування і заданого рівня істотності, скориставшись таблицею.

Знайдемо коефіцієнт детермінації і перевіримо адекватність отриманого рівняння лінійної регресії за критерієм Фішера. Коефіцієнт детермінації визначається наступним чином:

 (1.32)

Щільність зв’язку оцінюється індексом детермінації: R=, проте інтерпретується тільки R². Якщо коефіцієнт детермінації більше 0,6, то 60% варіації залежної величини пояснюється варіацією незалежного параметра кореляції і зв’язок є щільним.