Множественная зависимость

2. Множественная зависимость

С помощью коэффициентов парной корреляции проанализировать тесноту линейной связи между ценой и возрастом автомобиля, а также между ценой и мощностью двигателя. Проверить их значимость с надежностью 0,9.

Методом наименьших квадратов найти оценки коэффициентов множественной линейной регрессионной модели

.

Проверить статистическую значимость параметров и уравнения множественной регрессии с надежностью 0,9.

Рассчитать точечный и интервальный прогноз среднего значения цены поступивших автомобилей возраста 3 года и мощностью двигателя 165 л.с. с доверительной вероятностью 0,95.

3. Экономическая интерпретация

На основе полученных статистических характеристик провести содержательный экономический анализ зависимости цены автомобиля от его возраста и мощности двигателя.

Расчетная таблица:

№	y	X1	x2	x12	x22	y*x1	y*x2	y2	x1x2
1	6,8	6	93	36	8649	40,8	632,4	46,2	558
2	7,2	4	67	16	4489	28,8	482,4	51,8	268
3	4,3	6	57	36	3249	25,8	245,1	18,5	342
4	10,0	4	106	16	11236	40,0	1060,0	100,0	424
5	9,7	5	108	25	11664	48,5	1047,6	94,1	540
6	12,4	4	136	16	18496	49,6	1686,4	153,8	544
7	12,9	4	143	16	20449	51,6	1844,7	166,4	572
8	6,6	7	127	49	16129	46,2	838,2	43,6	889
9	11,2	3	93	9	8649	33,6	1041,6	125,4	279
10	11,2	4	111	16	12321	44,8	1243,2	125,4	444
11	8,3	6	124	36	15376	49,8	1029,2	68,9	744
12	5,6	6	81	36	6561	33,6	453,6	31,4	486
13	5,6	6	71	36	5041	33,6	397,6	31,4	426
14	6,4	6	88	36	7744	38,4	563,2	41,0	528
15	5,3	7	112	49	12544	37,1	593,6	28,1	784
16	4,0	7	88	49	7744	28,0	352,0	16,0	616
Сумма	127,5	85	1605	477	170341	630,2	13510,8	1141,9	8444

Коэффициенты парной корреляции:

 =  = -0,833

 = = 0,665

Проверка значимости:

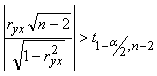
(по таблице).

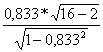 = 5,63 > 1,761

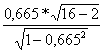 = 3,33 > 1,761

Коэффициенты корреляции существенно отличаются от 0.

Найдем матрицы:

 =

 =

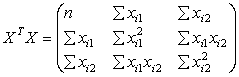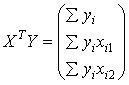Найдем матрицу , обратную к матрице . Определитель

|X^TX| = 16 * 477 * 170341 + 85 * 8444 * 1605 + 1605 * 85 * 8444 – 1605 * 477 * 1605 – 85 * 85 * 170341 – 16 * 8444 * 8444 = 3692086

Алгебраические дополнения:

D₁₁ = (–1)^{1 + 1} = 477 * 170341 – 8444² = 9951521 и т.д.

Матрица алгебраических дополнений

 =

Присоединенная матрица

(X^TX)^* = D^T =  = D

(матрица D симметрична).

(X^TX)^–1 = (X^TX)^* / |X^TX| =  =

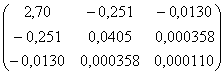
Вектор оценок коэффициентов модели:

A = (X^TX)^-1 (X^TY) =  =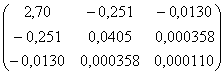

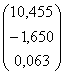
Y = 10,455 – 1,650x₁ + 0,063x₂

Расчетная таблица:

№	y	x1	x2		y -	(y - )2	y -	(y - )2
1	6,8	6,0	93,0	6,38	0,42	0,179	-1,2	1,4
2	7,2	4,0	67,0	8,05	-0,85	0,721	-0,8	0,6
3	4,3	6,0	57,0	4,12	0,18	0,031	-3,7	13,5
4	10,0	4,0	106,0	10,49	-0,49	0,241	2,0	4,1
5	9,7	5,0	108,0	8,97	0,73	0,539	1,7	3,0
6	12,4	4,0	136,0	12,37	0,03	0,001	4,4	19,6
7	12,9	4,0	143,0	12,81	0,09	0,009	4,9	24,3
8	6,6	7,0	127,0	6,86	-0,26	0,065	-1,4	1,9
9	11,2	3,0	93,0	11,33	-0,13	0,016	3,2	10,4
10	11,2	4,0	111,0	10,80	0,40	0,157	3,2	10,4
11	8,3	6,0	124,0	8,32	-0,02	0,000	0,3	0,1
12	5,6	6,0	81,0	5,63	-0,03	0,001	-2,4	5,6
13	5,6	6,0	71,0	5,00	0,60	0,361	-2,4	5,6
14	6,4	6,0	88,0	6,06	0,34	0,113	-1,6	2,5
15	5,3	7,0	112,0	5,92	-0,62	0,379	-2,7	7,1
16	4,0	7,0	88,0	4,41	-0,41	0,171	-4,0	15,8
Сумма	127,5					2,985		125,9

Остаточная дисперсия

S² = ∑ (y_i - _i)² / (n – m – 1) = 2,985 / (16 – 2 – 1) = 0,230

Ковариационная матрица:

S² (X^TX)^-1 = 0,230 *  =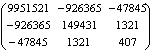

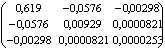
Стандартные ошибки коэффициентов равны квадратным корням из диагональных элементов ковариационной матрицы:

S₀ =  = 0,787

S₁ =  = 0,096

S₂ =  = 0,005

Проверим значимость параметров регрессии.

Табличное значение

t_{1 – α/2, n – 3} = 1,77

t₀ = |a₀| / S₀ = 10,455 / 0,787 = 13,3 > 1,77

t₁ = |a₁| / S₁ = 1,650 / 0,096 = 17,1 > 1,77

t₂ = |a₂| / S₂ = 0,063 / 0,005 = 12,4 > 1,77

Все параметры значимы.

Коэффициент детерминации

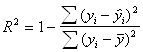 = 1 – 2,985 / 125,9 = 0,976

Табличное значение критерия Фишера

F_т = 3,8

Расчетное значение

F_ф =  =  = 267,7 > 3,8

Уравнение значимо.

Точечный прогноз:

(x^p) = 10,455 – 1,650 * 3 + 0,063 * 165 = 15,83 тыс. у.е.

Интервальный прогноз

Квантиль распределения Стьюдента (по таблице)

 = t_{0,975; 13} = 2,16

где S =  =  = 0,479

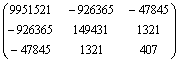
x^p (X^TX)^-1(x^p)^T =  =   = 0,633

 = 0,479 *  = 0,381

_В,Н = 15,83 ± 2,16 * 0,381 = 15,83 ± 0,68

_Н = 15,15

_В = 16,51

3. Экономическая интерпретация. Между возрастом автомобиля и его ценой существует тесная отрицательная связь (коэффициент корреляции –0,833): при увеличении возраста на 1 год (при фиксированной мощности двигателя) цена падает в среднем на 1,650 тыс. усл. ед.

Между мощностью двигателя и ценой автомобиля существует менее тесная положительная связь (коэффициент корреляции 0,665): при увеличении мощности на 1 л.с. (при фиксированном возрасте автомобиля) цена увеличивается в среднем на 0,063 тыс. усл. ед.

С вероятностью 0,95 можно утверждать, что цена автомобиля при возрасте 3 года и мощности двигателя 165 л.с. будет находиться в пределах от 15,15 до 16,51 тыс. усл. ед.

Задача 3