Навигация
1. Для регрессионной модели
и
с помощью критерия Дарбина-Уотсона проверить наличие или отсутствие автокорреляции на уровне значимости 0,05.
2. Для регрессионной модели
проверить наличие или отсутствие мультиколлинеарности, используя:
а) парный коэффициент корреляции;
б) критерий «хи-квадрат» χ2 на уровне значимости 0,05.
Расчетная таблица:
| № | et | et-1 | et - et-1 | (et - et-1)2 | (et)2 |
| 2 | -0,85 | 0,42 | -1,27 | 1,62 | 0,72 |
| 3 | 0,18 | -0,85 | 1,03 | 1,05 | 0,03 |
| 4 | -0,49 | 0,18 | -0,67 | 0,45 | 0,24 |
| 5 | 0,73 | -0,49 | 1,22 | 1,50 | 0,54 |
| 6 | 0,03 | 0,73 | -0,70 | 0,49 | 0,00 |
| 7 | 0,09 | 0,03 | 0,06 | 0,00 | 0,01 |
| 8 | -0,26 | 0,09 | -0,35 | 0,12 | 0,07 |
| 9 | -0,13 | -0,26 | 0,13 | 0,02 | 0,02 |
| 10 | 0,40 | -0,13 | 0,52 | 0,27 | 0,16 |
| 11 | -0,02 | 0,40 | -0,41 | 0,17 | 0,00 |
| 12 | -0,03 | -0,02 | -0,01 | 0,00 | 0,00 |
| 13 | 0,60 | -0,03 | 0,63 | 0,39 | 0,36 |
| 14 | 0,34 | 0,60 | -0,26 | 0,07 | 0,11 |
| 15 | -0,62 | 0,34 | -0,95 | 0,91 | 0,38 |
| 16 | -0,41 | -0,62 | 0,20 | 0,04 | 0,17 |
| Сумма | 7,11 | 2,81 |
Статистика Дарбина-Уотсона
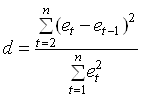= 7,11 / 2,81 = 2,53
Табличные значения при n = 16, m = 2
dl = 0,98; du = 1,54
Так как 4 – du < d < 4 – dl, вопрос о наличии автокорреляции остается открытым (область неопределенности критерия).
Найдем коэффициент парной корреляции между объясняющими переменными.
r12 = 
= -0,169
Проверим значимость коэффициента корреляции.
= 
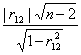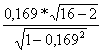= 0,643 < 1,761
Коэффициент незначим, т.е. мультиколлинеарность не имеет места.
Определитель матрицы коэффициентов парной корреляции:
Det (r) = 
= 1 – 0,1692 = 0,971
Табличное значение статистики для df = 1 и α = 0,05 равно
χ21;0,05 = 3,84.
Фактическое значение статистики
= - (16 – 1 – (2 * 2 + 5) / 6) ln 0,971 = 0,39 < 3,84
Мультиколлинеарность не имеет места, т.е. линейной зависимости между объясняющими переменными (возрастом автомобиля и мощностью двигателя) не существует. Это свидетельствует о надежности оценок параметров модели.
Похожие работы
... системы цен по остальным товарам. Конец XIX – начало XX века ознаменовались широким использованием математики в экономике. В XX в. математические методы моделирования используются столь широко, что почти все работы, удостоенные Нобелевской премии по экономике, связаны с их применением (Д. Хикс, Р. Солоу, В. Леонтьев, П. Самуэльсон, Л. Канторович и др.). Развитие предметных дисциплин в большинстве ...
... моделей экстремальных планов и экстремальных значений целевой функции быть не может. Таким образом, для принятия оптимального решения любой экономической задачи необходимо построить ее экономико-математическую модель, по структуре включающую в себе систему ограничений, целевую функцию, критерий оптимальности и решение. Методика построения экономико-математической модели состоит в том, чтобы ...
... Ю.Н. Математические методы в экономике: Учебник.2-е изд. – М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. – 368 с. 7. Монахов А.В. Математические методы анализа экономики. – Спб: Питер, 2002. – 176 с. 8. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов /В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др., Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. ...
... , что найденный вариант является наилучшим. В современных условиях даже не значительные ошибки могут привести к огромным потерям. В связи с этим возникла необходимость привлечения к анализу и синтезу экономических систем оптимизационных экономико-математических методов и ЭВМ, что создает основу для принятия научно обоснованных решений. Такие методы объединяют в одну группу под общим названием « ...
0 комментариев