Навигация
Постановка задач оптимизации
2.2. Постановка задач оптимизации
В общем виде задача оптимизации, или задача определения экстремума, ставится следующим образом.
Пусть заданы:
функция f(X), определенная на множестве O Í RN;
множество D Í RN.
Найти точку Y = (y1, y2,..., yN) Î D, в которой функция f (X) достигает экстремального (минимального или максимального) значения, т.е.
f(X) = extr f(X) и Y Î D.
Функция f(X) называется целевой функцией, переменные X – управляемыми переменными, D – допустимым множеством и любой набор значений Y управляемых переменных, принадлежащий D (Y Î D), - допустимым решением задачи оптимизации.
Понятно, что искомая точка Y, в которой f(X) достигает своего экстремума, должна принадлежать пересечению области определения O функции f(X) и допустимого множества D (YÎ O Ç D). Если множества O и D совпадают со всем пространством RN(O = D = RN), то такая задача называется задачей на безусловный экстремум. Если хотя бы одно из множеств O или D является собственным подмножеством пространства RN(O Ì RN , D Ì RN) или множества O и D пересекаются (O Ç D ¹ Æ), то такая задача называется задачей на условный экстремум, в противном случае (O Ç D = Æ) точка экстремума Y не существует. Подчеркнем один частный случай: если множества O и D пересекаются в одной точке Y, то эта точка Y является единственным допустимым решением.
Обычно в задаче условного экстремума задается не само допустимое множество решений D, а система соотношений, его определяющая,
yj(x1, х 2, хN) £ (=, ³) 0, j = 1, 2, … М,
т.е.
D = {X: yj (X) £ (=, ³) 0, j = 1, 2, ... , M} Í RN,
или множество D может одновременно задаваться как в явном виде, т.е. допустимое решение Х должно принадлежать некоторой области P Ì RN, так и системой ограничений.
III. Методы линейного программирования.
3.1. Общая и типовая задача в линейном программировании.
Оптимизационная задача – это экономико-математическая задача, которая состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений.
В самом общем виде задача математически записывается так:
U = f(X) ® max; X Î W,
Где X = (Х1, Х2,…, Хn);
W – область допустимых значений переменных Х1, Х2,…, Хn;
f(X) – целевая функция.
Для того, чтобы решить задачу оптимизации, достаточно найти ее оптимальное решение, т.е. указать X() Î W такое, что f(X()) ³ f(X), при любом X Î W, или для случая минимизации - что f(X()) ≤ f(X), при любом X Î W.
Оптимизационная задача является неразрешимой, если она не имеет оптимального решения. В частности, задача максимизации будет неразрешима, если целевая функция f(X) не ограничена сверху на допустимом множестве W.
Методы решения оптимизационных задач зависят как от вида целевой функции f(X), так и от строения допустимого множества W. Если целевая функция в задаче является функцией n переменных, то методы решения называют методами математического программирования.
В математическом программировании принято выделять следующие основные задачи в зависимости от вида целевой функции f(X) и от области W:
· задачи линейного программирования, если f(X) и W линейны;
· задачи целочисленного программирования, если ставится условие целочисленности переменных Х1, Х2,…, Хn;
· задачи нелинейного программирования, если форма f(X) носит нелинейный характер.
Задачи линейного программирования.
Задачей линейного программирования называется задача исследования операций, математическая модель которой имеет вид:
f(X) = å СjXj ® max(min);
å aij xj = bi, iÎI, IÍM = {1, 2,…m};
å aij xj £ bi, iÎM;
Xj³0, jÎJ, JÍN = {1, 2,…n}.
При этом система линейных уравнений и неравенств, определяющая допустимое множество решений задачи W, называется системой ограничений задачи линейного программирования, а линейная функция f(X) называется целевой функцией или критерием оптимальности.
Любую задачу линейного программирования можно свести к задаче линейного программирования в канонической форме. Для этого в общем случае нужно уметь сводить задачу максимизации к задаче минимизации; переходить от ограничений неравенств к ограничениям равенств и заменять переменные, которые не подчиняются условию неотрицательности. Максимизация некоторой функции эквивалентна минимизации той же функции, взятой с противоположным знаком, и наоборот.
Правило приведения задачи линейного программирования к каноническому виду состоит в следующем:
1) если в исходной задаче требуется определить максимум линейной функции, то следует изменить знак и искать минимум этой функции;
2) если в ограничениях правая часть отрицательна, то следует умножить это ограничение на -1;
3) если среди ограничений имеются неравенства, то путем введения дополнительных неотрицательных переменных они преобразуются в равенства;
4) если некоторая переменная Хk не имеет ограничений по знаку, то она заменяется (в целевой функции и во всех ограничениях) разностью между двумя новыми неотрицательными переменными::
Xk = X`k – Xl, где l – свободный индекс, X`k ³ 0, Xk ³ 0.
Похожие работы
... Ю.Н. Математические методы в экономике: Учебник.2-е изд. – М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. – 368 с. 7. Монахов А.В. Математические методы анализа экономики. – Спб: Питер, 2002. – 176 с. 8. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов /В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др., Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. ...
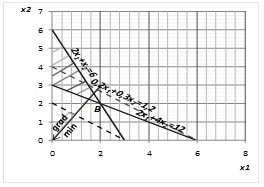
... решений целевая функция принимает в точке (0; 6), и это значение равно . рис. 1 - Графическое решение задачи линейного программирования ЗАДАЧА 2 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования Для изготовления четырех видов продукции используют три вида сырья. ...
... модели по тем свойствам, которые выбраны в качестве существенных (другими словами, должны быть произведены верификация и валидация модели). Применение численных результатов моделирования в экономике направлено на решение практических задач (анализ экономических объектов, экономическое прогнозирование развития хозяйственных и социальных процессов, выработка управленческих решений на всех уровнях ...
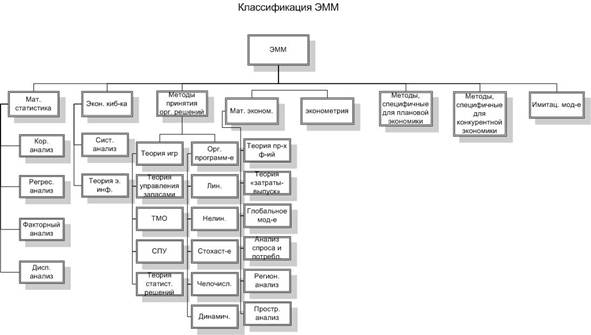
... , что найденный вариант является наилучшим. В современных условиях даже не значительные ошибки могут привести к огромным потерям. В связи с этим возникла необходимость привлечения к анализу и синтезу экономических систем оптимизационных экономико-математических методов и ЭВМ, что создает основу для принятия научно обоснованных решений. Такие методы объединяют в одну группу под общим названием « ...
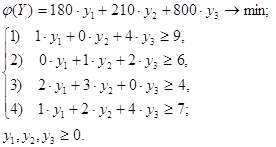


0 комментариев