Навигация
Постановка задачи линейного программирования
3.2. Постановка задачи линейного программирования
Под термином «транспортные задачи» понимается широкий круг задач не только транспортного характера. Общим для них является, как правило, распределение ресурсов, находящихся у m производителей (поставщиков), но n потребителям этих ресурсов.
На автомобильном транспорте часто встречаются следующие задачи, относящиеся к транспортным:
· прикрепление потребителей ресурса к производителям;
· привязка пунктов отправления к пунктам назначения;
· взаимная привязка грузопотоков прямого и обратного направлений;
· отдельные задачи оптимальной загрузки промышленного оборудования;
· оптимальное распределение объемов выпуска промышленной продукции между заводами-изготовителями.
Транспортным задачам присущи следующие особенности:
· распределению подлежат однородные ресурсы;
· условия задачи описываются только уравнениями;
· все переменные выражаются в одинаковых единицах измерения;
· во всех уравнениях коэффициенты при неизвестных равны единице;
· каждая неизвестная встречается только в двух уравнениях системы ограничений.
Транспортные задачи могут решаться симплекс-методом.
3.3. Решение транспортной задачи
| Мощности постав- щиков 140 | Мощности потребителей | U i | ||||
| 18 | 15 | 32 | 45 | 30 | ||
| 30 | 10 | 7/15 | 14 | 8/5 | 7/10 | 0 |
| 40 | 12 | 8 | 10 | 8/40 | 15 | 0 |
| 25 | 6/18 | 10 | 10 | 12 | 14/7 | -7 |
| 45 | 16 | 10 | 8/32 | 12 | 16/13 | -9 |
| Vj | -1 | 7 | -1 | 8 | 7 | |
Начальное распределение выберем по методу наименьших стоимостей. Порядок заполнения клеток: (3,1), (1,2), (4,3). (2,4), (1,5), (1,4), (3,5), (4,5)
Суммарные затраты:
f(x) = 6´18+7´15+8´32+8´5+8´40+7´10+14´7+16´13=1107
Рассмотрим процесс нахождения потенциалов для данного распределения.
Положим, Ui=0 Þ V2=U1+C12=7; V5=U1+C15=7=U3+14=U4+16 Þ U3= -7, U4= -9; V3=U4+C43= -1; V4=U2+8=U1+8 Þ U2=U1=0; V4=8.
Найдем оценки: dij=(Ui+cij)-Vj:
11 0 15 0 0
(dij) = 13 1 11 0 8
0 -4 4 -3 0
8 -6 0 -5 0
Данный план не является оптимальным, т.к. есть отрицательные оценки.
Построим контур перераспределения для клетки (4,2). Наименьшая поставка в вершине контура со знаком “-” равна 13, поэтому проведем перераспределение поставок, уменьшив поставки в клетках со знаком “-” на 13 и увеличив поставки в клетках со знаком “+” на 13. результаты поставлены в таблице 2.
| Мощности постав- щиков 140 | Мощности потребителей | U i | ||||
| 18 | 15 | 32 | 45 | 30 | ||
| 30 | 10 | 7/2 | 14 | 8/5 | 7/23 | 0 |
| 40 | 12 | 8 | 10 | 8/40 | 15 | 0 |
| 25 | 6/18 | 10 | 10 | 12 | 14/7 | -7 |
| 45 | 16 | 10/13 | 8/32 | 12 | 16 | -3 |
| Vj | -1 | 7 | 5 | 8 | 7 | |
Суммарные затраты:
f(x) = 6´18+7´2+10´13+8´32+8´5+8´40+7-23+14-7=1127
Положим U1=0
V2 = U1+C12=7=U4+10 Þ U4 = -3
V3 = U4+8=5; V4=U1+8=8=U2+8 Þ U2=0
V5 = U1+7= 7 = U3+14 Þ U3= -7
V1 = U3+6= -1
dij = (Ui+Cij)-Vj
9 0 9 0 0
(dij) = 11 1 5 0 8
0 -3 -2 -3 0
14 0 0 1 6
Наличие отрицательных оценок свидетельствует о том, что план не является оптимальным. Построим контур перераспределения для клетки (3,2). Наименьшая поставка в вершине контура со знаком “-” равна 2. Произведем перераспределение поставок. Результаты представим в таблице 3.
| Мощности постав- щиков 140 | Мощности потребителей | U i | ||||
| 18 | 15 | 32 | 45 | 30 | ||
| 30 | 10 | 7 | 14 | 8/5 | 7/25 | 0 |
| 40 | 12 | 8 | 10 | 8/40 | 15 | 0 |
| 25 | 6/18 | 10/2 | 10 | 12 | 14/5 | -7 |
| 45 | 16 | 10/13 | 8/32 | 12 | 16 | -7 |
| Vj | -1 | 7 | 5 | 8 | 7 | |
Суммарные затраты:
f(x) = 6´18+10´2+10´13+8´32+8´5+8´40+7´25+14´7=1119
Положим, U1=0 Þ V4=8, V5=7; V4=U2+8 Þ U2=0
V5 = U3+14 Þ U3= 7-14= -7; V1= -7+6= -1; V2= -7+10= +3
V2=U4+10 Þ U4=3-10= -7; v3= -7+8=1
9 4 13 0 0
(dij) = 13 5 9 0 8
2 0 2 -3 0
10 0 0 -3 2
Наличие отрицательных оценок свидетельствует о том, что план не является оптимальным. Построим контур перераспределения для клетки (3,4).
Наименьшая поставка в клетке со знаком “-” равна 5. Произведем перераспределение поставок результаты представим в таблице 4.
| Мощности постав- щиков 140 | Мощности потребителей | U i | ||||
| 18 | 15 | 32 | 45 | 30 | ||
| 30 | 10 | 7 | 14 | 8 | 7/30 | 0 |
| 40 | 12 | 8 | 10 | 8/40 | 15 | 0 |
| 25 | 6/18 | 10/2 | 10 | 12/5 | 14 | -4 |
| 45 | 16 | 10/13 | 8/32 | 12 | 16 | -4 |
| Vj | 2 | +6 | 4 | 8 | 7 | |
Суммарные затраты:
f(x) = 7´30+8´40+6´18+10´2+12´5+10´13+8´32=1104
U1=0 Þ V5= 7; U2=0 Þ V4=8=U3+12 Þ U3=-4 Þ
V1= 6-4=2, V2=10-4=+6=U4+10; V3= -4+8= +4
8 1 10 0 0
(dij) = 10 2 6 0 8
0 0 2 0 3
10 0 0 0 5
Матрица оценок (dij) не содержат отрицательных величин Þ данный план является оптимальным, т.к. С34 = 0, а клетка (3,4) не является запятой, то данный план не является единственным. Стоимость перевозок по этому плану, как было рассчитано ранее, равна f(x) = 1104.
3.6. Симплекс-метод решения задач линейного программирования.
Симплекс-метод позволяет отказаться от метода перебора при решении задач линейной оптимизации, является основным численным методом решения задач линейного программирования и позволяет за меньшее число шагов, чем в методе перебора, получить решение.
Реализация алгоритма симплекс-метода.
1. Записать задачу в канонической форме: заменить все ограничения-неравенства с положительной правой;
2. Разделить переменные на базисные и свободные: перенести свободные переменные в правую часть ограничений-неравенств.
3. Выразить базисные переменные через свободные: решить систему линейных уравнений (ограничений-неравенств) – относительно базисных переменных;
4. Проверить неотрицательность базисных переменных: убедиться в неотрицательности свободных членов в выражениях для базисных переменных. Если это не так, вернуться к пункту 2, выбирая другой вариант разделения переменных на базисные и свободные.
5. Выразить функцию цели через свободные переменные: базисные переменные, входящие в функцию, выразить через свободные переменные;
6. Вычислить полученное базисное решение и функцию цели на нем: приравнять к 0 свободные переменные;
7. проанализировать формулу функции цели: если все коэффициенты свободных переменных положительны (отрицательны), то найденное базисное решение будет минимально (максимально) и задача считается решенной;
8. Определить включаемую в базис и исключаемую из базиса переменные: если не все коэффициенты при свободных переменных в функции цели положительны (отрицательны), то следует выбрать свободную переменную, входящую в функцию цели с максимальным по модулю отрицательным (положительным) коэффициентом, и увеличивать ее до тех пор, пока какая-нибудь из базисных переменных не станет равной 0. Свободную переменную рассматриваем как новую базисную переменную (включаемую в базис), а базисную переменную рассматриваем как новую базисную переменную (исключаемую из базиса);
9. Используя новое разделение переменных на базисное и свободное, вернуться к пункту 3 и повторять все этапы до тех пор, пока не будет найдено оптимальное решение.
В заключение отметим, что определение оптимального решения распадается на два этапа:
· Нахождение какого-либо допустимого решения с положительным свободным членом;
· Определение оптимального решения, дающего экстрему целевой функции.
IV. Методы нелинейного программирования.
Похожие работы
... Ю.Н. Математические методы в экономике: Учебник.2-е изд. – М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. – 368 с. 7. Монахов А.В. Математические методы анализа экономики. – Спб: Питер, 2002. – 176 с. 8. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов /В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др., Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. ...
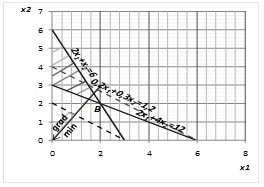
... решений целевая функция принимает в точке (0; 6), и это значение равно . рис. 1 - Графическое решение задачи линейного программирования ЗАДАЧА 2 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования Для изготовления четырех видов продукции используют три вида сырья. ...
... модели по тем свойствам, которые выбраны в качестве существенных (другими словами, должны быть произведены верификация и валидация модели). Применение численных результатов моделирования в экономике направлено на решение практических задач (анализ экономических объектов, экономическое прогнозирование развития хозяйственных и социальных процессов, выработка управленческих решений на всех уровнях ...
... , что найденный вариант является наилучшим. В современных условиях даже не значительные ошибки могут привести к огромным потерям. В связи с этим возникла необходимость привлечения к анализу и синтезу экономических систем оптимизационных экономико-математических методов и ЭВМ, что создает основу для принятия научно обоснованных решений. Такие методы объединяют в одну группу под общим названием « ...


0 комментариев