Навигация
Построить баланс (заполнить таблицу) производства и распределения продукции предприятий холдинга
2. Построить баланс (заполнить таблицу) производства и распределения продукции предприятий холдинга.
| предприятия | коэффициенты прямых затрат | конечный продукт | ||
| 1 | 2 | 3 | ||
| 1 | 0,2 | 0,1 | 0,2 | 150 |
| 2 | 0 | 0,1 | 0,2 | 180 |
| 3 | 0,1 | 0 | 0,1 | 100 |
Решение:
Найдем продуктивность А с помощью достаточного условия ||A||max(0,3;0,2;0,5)=0,5<1
Следовательно матрица А продуктивна
Подготовим таблицу матричного баланса
| предприятия | конечный | валов. пр | |||
| 1 | 2 | 3 | |||
| 1 | 50,22293 | 23,08917 | 27,80255 | 150 | 251,1146 |
| 2 | 0 | 23,08917 | 27,80255 | 180 | 230,8917 |
| 3 | 25,11146 | 0 | 13,90127 | 100 | 139,0127 |
| усл. ч. пр. | 175,7803 | 184,7134 | 69,50637 | 430=430 | |
| вал. вып | 251,1146 | 230,8917 | 139,0127 | 621,0191=621,0191 |
Используем соотношение Х=(Е-А)’*У, полученное в соответствие модели Леонтьева для определения валового выпуска для этого найдем: (Е-А)’ – матрицу полных затрат (Е – единичная матрица),
|
| 0 |
|
| ||||||||
| Е = 0 | 1 | 0 |
| ||||||||
| 0 | 0 | 1 |
| ||||||||
|
|
| ||||||||||
| 1 | 0 |
|
| 0,1 |
|
| 0,8 | -0,1 |
| ||
| Е-А= | 0 | 1 | 0 | - | 0 | 0,1 | 0,2 | = | 0 | 0,9 | -0,2 |
| 0 | 0 | 1 | 0,1 | 0 | 0,1 | -0,1 | 0 | 0,9 | |||
Найдем обратную матрицу (Е-А)’ используя функцию в Excel (fx/математическая/МоБР),
|
| 0,143312 |
| |
| (Е-А)’= | 0,031847 | 1,11465 | 0,254777 |
| 0,143312 | 0,015924 | 1,146497 |
Найдем величины валовой продукции, используя в Excel (fx/математическая/МУМНОЖ)
|
| 1,289809 | 0,143312 |
|
|
| ||
| (E-A)’*Y= | 0,031847 | 1,11465 | 0,254777 | * | 180 | = | 230,8917 |
| 0,143312 | 0,015924 | 1,146497 | 100 | 139,0127 |
Рассчитаем величины производственных затрат по формуле
Xij=aij*xj
aij- технологическая матрица
xj-строка валового выпуска,
| Х11=0,2*251,1146=50,22293 | Х12=0,1*230,8917=23,08917 | Х13=0,2*139,0127=27,80255 |
| Х21=0*251,1146=0 | Х22=0,1*230,8917=23,08917 | Х23=0,2*139,0127=27,80255 |
| Х31=0,1*251,1146=25,11146 | Х32=0*230,8917=0 | Х33=0,1*139,0127=13,90127 |
| Для расчета величин условно чистой продукции используем соотношение баланса для производства: Z=xj-∑xij |
| xij – по столбцу Z1=251.1146-(50.22293+0+25.11146)=175.7803 Z2=230.8917-(23.08917+23.08917+0)=184.7134 Z3=139.0127-(27.80255+27.80255+13.90127)=69.50637 |
Проверим баланс конечной и условно чистой продукции
∑YI=∑ZJ, ∑Xi=∑Xj,
Z=175.7803+184.7134+69.50637=430 =Y=150+180+100=430
Xi=251.1146+230.8917+139.0127=621.0191=Xj=251.1146+230.8917+139.0127=621.0191
Заполняем таблицу, подготовленную выше, матричного баланса полученными данными.
4. В течение девяти последовательных недель фиксировался спрос У(t) (млн. руб.) на кредитные ресурсы финансовой компании. Временной ряд Y(t) этого показателя приведен в таблице.
| Недели | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Спрос на кредитные ресурсы | 3 | 7 | 10 | 11 | 15 | 17 | 21 | 25 | 23 |
Требуется:
1. Проверить наличие аномальных наблюдений.
2. Построить линейную модель Y(t)=a0+a1t параметры которой оценить МНК (Y(t) – расчетные, смоделированные значения временного ряда).
3. Оценить адекватность построенных моделей, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использовании R\S- критерия взять табулированные границы 2,7-3,7).
4. Оценить точность моделей на основе использования средней относительной ошибки аппроксимации.
5. По двум построенным моделям осуществить прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитывать при доверительной вероятности р=70%)
6. Фактические значения показателя, результаты моделирования и прогнозирования представить графически.
Решение:
| Недели | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Спрос на кредитные ресурсы | 3 | 7 | 10 | 11 | 15 | 17 | 21 | 25 | 23 |
Построим график:
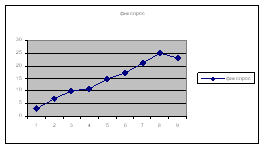
Проверим на анормальность - 9 неделю, у9=23
Оставшиеся наблюдения
| Недели | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Спрос на кредитные ресурсы | 3 | 7 | 10 | 11 | 15 | 17 | 21 | 25 |
Для оставшихся рассчитаем: уср - среднее значение; Sy – средне квадратичное отклонение, используя функции Excel;
Вычислим статистику Стьюдента – tнаб=| y*-yср|/Sy
уср= 13,625 (fx/статистические/СРЗНАЧ)
Sy= 6,836254457 (fx/статистическая/СТАНДОТКЛОН)
При L=5%, K=n-2=9-2=7,
tкр= 2,36462256 (fx/статистическая/СТЬЮДРАСПОБР)
tнаб= |23-13,625|/6,84=1,371364986
tнаб=1,37<tкр=2,36
Следовательно, наблюдаемое у9 не является аномальной и не требует замены.
С помощью программы РЕГРЕССИИ (в Excel сервис/анализ данных/РЕГРЕССИЯ) рассчитаем и получим:
| Регрессионная статистика | |
| Множественный R | 0,983716989 |
| R-квадрат | 0,967699115 |
| Нормированный R-квадрат | 0,963084703 |
| Стандартная ошибка | 1,444200224 |
| Наблюдения | 9 |
| Дисперсионный анализ | |||||
| df | SS | MS | F | Значимость F | |
| Регрессия | 1 | 437,4 | 437,4 | 209,7123 | 1,78531E-06 |
| Остаток | 7 | 14,6 | 2,085714286 | ||
| Итого | 8 | 452 | |||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y-пересечение | 1,166667 | 1,049187 | 1,111971949 | 0,302876 | -1,31426491 | 3,648 | -1,3143 | 3,6475982 |
| Переменная X 1 | 2,7 | 0,186445 | 14,48144774 | 1,79E-06 | 2,259126889 | 3,141 | 2,25913 | 3,1408731 |
| ВЫВОД ОСТАТКА | ||
| Наблюдение | Предсказанное Y | Остатки |
| 1 | 3,866667 | -0,866666667 |
| 2 | 6,566667 | 0,433333333 |
| 3 | 9,266667 | 0,733333333 |
| 4 | 11,96667 | -0,966666667 |
| 5 | 14,66667 | 0,333333333 |
| 6 | 17,36667 | -0,366666667 |
| 7 | 20,06667 | 0,933333333 |
| 8 | 22,76667 | 2,233333333 |
| 9 | 25,46667 | -2,466666667 |
Модель построена, ее уравнение уt=a+b*t, t-момент времени, уt- теоретическое моделирование значения У, а,b- коэффициенты модели
a=1.166666667, b=2.7, следовательно уt=1,166666667+2,7t
коэффициент регрессии b=2,7, т. е. с каждым годом спрос на кредитные ресурсы финансовой компании в среднем возрастают на 2,7 млн. руб.
Рассмотрим столбец Остатки и построим с помощью «мастер диаграмм» в Excel график остатков:
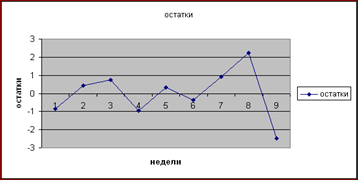
1 подсчитаем количество поворотных точек р для рядов остатков – р=5
2 критическое количество определим формулой - ркр=[2*(n-2)/3-1,96*√16*n-29/90]
[ ] – целая часть; n- количество исходных данных
ркр=[2*(9-2)/3-1,96*√16*9-29/90]=2,451106=2
3 сравним фактическое р с ркр
р=5 > ркр=2 следовательно, свойство случайности выполняется.
Для проверки независимости уровней ряда остатков:
Похожие работы
... ai- расход сырья на единицу продукции; B - общий запас сырья; W - область допустимых ограничений; Тема 2. Метод математического моделирования в экономике. 2.1. Понятие “модель” и “моделирование”. С понятием “моделирование экономических систем” (а также математических и др.) связаны два класса задач: 1) задачи анализа, когда система подвергается глубокому изучению ее ...
... отрезка времени. Как правило, это задача, решение которой влечет за собой постановки близких или аналогичных задач. Глава 2. Экономико-математическое моделирования процессов принятия управленческих решений. В классификации решений по времени действия выражается принцип их цикличности, определенная хронологическая последовательность, временные рамки которой неизбежно должны учитываться в процессе ...
... производственной функции, моделей поведения фирмы, моделей общего экономического равновесия, прежде всего модели Л. Вальраса и ее модификаций. Глава 2. История развития экономико-математического моделирования в США Для характеристики математического направления в экономике за последние 80 – 90 лет приведу лишь некоторые результаты, сыгравшие заметную роль в его развитии. Как в теоретическом, ...
... вопросы должны быть получены в ходе маркетинговых и проектно-изыскательских работ на фазе проектирования спортивных сооружений. И уже на этой стадии в процесс активно включаются экономико-математические методы, задействуется существующий аппарат математического моделирования и прогнозирования. Данные методы и расчеты совершенно необходимы для определения: сроков окупаемости отдельных предприятии ...

0 комментариев