Энтропия

СОДЕРЖАНИЕ

Введение

§1. Понятие энтропии. Энтропия как мера степени неопределенности

§2. Понятие об информации. Измерение информации

§3. Теорема Шеннона о кодировании при наличии помех

§4. Пример использования энтропии в прогнозировании и ее значение для прогнозирования. Применение к рискам

Заключение

Список использованной литературы

Введение

Предметом работы является энтропия и информация. Целью данной работы является изучение энтропии, информации и применения данных понятий к рискам. Поставленная цель ставит решение следующих задач: рассмотрения понятия энтропии, статистического смысла данного понятия, энтропии как меры степени неопределенности, понятия об информации, теоремы Шеннона о кодировании при наличии помех, использования энтропии в прогнозировании и применения энтропии к рискам.

Данная тема актуальна, так как трудно найти понятия более общие для всех наук (не только естественных) и, вместе с тем, иногда носящих оттенок загадочности, чем энтропия и информация. Отчасти это связано с самими названиями. Если бы не звучное название “энтропия” осталась бы с момента первого рождения всего лишь “интегралом Клаузиуса”, вряд ли она бы не рождалась вновь и вновь в разных областях науки под одним именем. Кроме того, ее первооткрыватель Клаузиузус, первым же положил начало применению введенного им для, казалось бы узкоспециальных термодинамических целей понятия к глобальным космологическим проблемам (тепловая смерть Вселенной). С тех пор энтропия многократно фигурировала в оставшихся навсегда знаменитыми спорах. В настоящее время универсальный характер этого понятия общепризнан и она плодотворно используется во многих областях.

Термин “информация” замечателен тем, что, существующему с давних пор бытовому понятию, К.Шенноном был придан математически точный смысл. Неопределенно-бытовой смысл этого термина уже научного. Это приводило и приводит ко многим недоразумениям/ Данную тему опишем с помощью следующих методов: синтеза, анализа, индукции, дедукции, сравнения и расчетного метода.

Работа изложена на 26 страниц и состоит из четырех параграфов. В работе 1 таблица и 7 примеров.

§1. Понятие энтропии. Статистический смысл понятия энтропии. Энтропия как мера степени неопределенности

Энтропия (от греч. entropia - поворот, превращение) - мера неупорядоченности больших систем. Впервые понятие "энтропия" введено в XIX в. в результате анализа работы тепловых машин, где энтропия характеризует ту часть энергии, которая рассеивается в пространстве, не совершая полезной работы (отсюда определение: энтропия - мера обесценивания энергии). Затем было установлено, что энтропия характеризует вероятность определенного состояния любой физической системы среди множества возможных ее состояний. В закрытых физических системах все самопроизвольные процессы направлены к достижению более вероятных состояний, т. е. к максимуму энтропии . В равновесном состоянии, когда этот максимум достигается, никакие направленные процессы невозможны. Отсюда возникла гипотеза о тепловой смерти Вселенной. Однако распространение на всю Вселенную законов, установленных для закрытых систем, не имеет убедительных научных оснований. В XX в. понятие " энтропия " оказалось плодотворным для исследования биосистем, а также процессов передачи и обработки информации. Эволюция в целом и развитие каждого организма происходит благодаря тому, что биосистемы, будучи открытыми, питаются энергией из окружающего мира. Но при этом биопроцессы протекают таким образом, что связанные с ними "производство энтропии " минимально. Это служит важным руководящим принципом и при разработке современных технологических процессов, при проектировании технических систем. Количественная мера информации формально совпадает с "отрицательно определенной " энтропией. Но глубокое понимание соответствия энтропии физической и информационной остается одной из кардинальных недостаточно исследованных проблем современной науки. Ее решение послужит одним из важных факторов становления нового научно-технического мышления.

Энтропия широко применяется и в других областях науки: в статистической физике как мера вероятности осуществления какого-либо макроскопического состояния; в теории информации как мера неопределенности какого-либо опыта (испытания), который может иметь разные исходы. Эти трактовки имеют глубокую внутреннюю связь. Например, на основе представлений об информационной энтропии можно вывести все важнейшие положения статистической физики.

Теория информации возникла для описания передачи и приёма сообщений в процессе деятельности человека. Во всех её задачах присутствуют понятия передатчика и приёмника, сигнала-сообщения, событий и их вероятностей. Существование цели передачи информации в теории информации выражается тем, что вводится понятие известного заданного события. Для него может быть определена вероятность р₀  наступления до приёма сообщения и  р₁  после приёма.

В силу определения информации как устранённой неопределённости в достижении цели строгая (то есть математическая) формализация понятия об информации требует выразить математическим соотношением, что есть неопределённость в достижении цели.

Существование неопределённости связано с участием вероятностей в осуществлении событий. Устранение неопределённости есть увеличение вероятности наступления того, что задано как цель. Поэтому вероятности должны участвовать в математической формулировке величины устранённой неопределённости.

Первая удачная попытка реализовать определение информации на такой основе осуществлена в 1928 г. Л. Хартли. Пусть возможно в данных условиях  n  вариантов некоторого результата. Целью является один из них. Хартли предложил характеризовать неопределённость логарифмом числа  n.  То есть  log n  является количественной мерой неопределённости. Выбор основания логарифма связан с понятием об алфавитах для описания информации. Этот выбор существенен для экономичности кодирования в технических устройствах или живых системах (сокращения потоков импульсов или аналоговых сигналов), но не меняет самого количества информации как устранённой неопределённости за счёт того, что перед логарифмом вводится безразмерный множитель, выражаемый модулем перехода между основаниями логарифмов. От него зависят названия единиц информации.

При математическом описании неопределённости (например способом Хартли) в случае равновероятных результатов можно перейти от их числа  n  к обратной величине - вероятности  р  одного из них. В терминах связи конкретно говорят о вероятности переданного сообщения  р₀  у приёмника до приёма сообщения. Устранение неопределённости выражается тем, что вероятность переданного сообщения у приёмника после приёма сигнала возрастает и становится  р₁ .  Тогда количественная мера  s  полученной информации (устранённой неопределённости) выражается логарифмом отношения вероятностей:

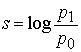
Оно равноправно по отношению к любому конкретному сообщению и имеет разную величину в зависимости от величин  р₀  и  р₁  для него. В частном случае, когда при передаче полностью отсутствую шумы и сбои, искажающие сигнал, вероятность  р₀  равна единице.

Недостаток этого определения в том, что оно справедливо в приближении равновероятности всех исходов. Это выполняется далеко не всегда. В пределе в этом определении невероятному исходу приравнивается неизбежный. В 1948 г. это исправил К. Шеннон, который определил в качестве меры неопределённости выражение:

где

есть вероятности отдельных исходов. Он предложил называть эту величину "энтропией", не поясняя связей и различий этого термина с общеизвестой энтропией в физике. Знак минус в предыдущей формуле отражает тот факт, что вероятности всегда меньше единицы, а энтропия знакопостоянная функция, для которой привычно задан положительный знак. Определение Шеннона сокращённо зависывают в виде:

,

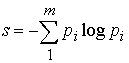подразумевая как очевидное, что признаки (аргументы), по отношению к которым определены события и их вероятности, могут быть существенно разными, а в эта формула (суммирование в ней) справедлива только для однородных признаков.

§2. Понятие об информации. Измерение информации

Понятие информации (informatio - разъяснение, осведомление, изложение) является одним из основных, ключевых понятий не только в информатике (в информологии - области знаний, изучающей проявление информации, её представление, измерение и т.д.), но и в математике, в физике и др. Понятие “информация” - плохо формализуемое и структурируемое понятие. В силу его всеобщности, объёмности, расплывчатости оно часто понимается неточно и неполно не только обучаемыми. Как правило, это понятие в курсе информатики не определяется, принимается как исходное базовое понятие, неопределяемый терм.

Информация трактуется по разному, например, как:

• любая сущность, которая вызывает изменения в некоторой информационно-логической (инфологической - состоящей из данных, знаний, абстракций и т.д.) модели системы (математика, системный анализ);

• сообщения, полученные системой от внешнего мира в процессе адаптивного управления, приспособления (теория управления, кибернетика);

• отрицание энтропии, отражение меры хаоса в системе (термодинамика);

• связи, устраняющие неопределённость в системе (теория информации);

• вероятность выбора в системе (теория вероятностей);

• отражение разнообразия в системе (физиология, биокибернетика);

• отражение материи, атрибут сознания, “интеллекта” системы (философия).

Но существует более полное понятие. Информация - это некоторая последовательность (налицо упорядоченность) сведений, знаний, которые актуализируемы (получаемы, передаваемы, преобразуемы, сжимаемы или регистрируемы) с помощью некоторых знаков (символьного, образного, жестового, звукового, сенсомоторного типа). Это приращение, развитие, актуализация знаний, возникающее в процессе целеполагающей интеллектуальной деятельности человека. Никакая информация, никакое знание не появляется сразу - этому предшествует этап накопления, осмысления, систематизации опытных данных, взглядов. Знание - продукт такого процесса. Мышление - необходимый атрибут такого процесса.

Информация может существовать в пассивной (не актуализированной) и активной (актуализированной) форме.

Пример. Информация актуализируется сообщениями, при этом формы облачения информации в сообщения различны, например, для живых существ - сигналы, жесты, для технических устройств - сигналы. Информация передаваемая от одного человека другому, может передаваться символами (письмо), жестами (сигнальщик на боевом корабле), звуками (диктор), геометрическими фигурами (чертёжник), художественными образами (балерина). Информация передающаяся животными может быть передана звуками (лай, вой, писк), ситуационным поведением (образами). Информация в технических устройствах, автоматах может быть передана электрическими, магнитными, световыми импульсами, как это происходит в ЭВМ.

Информация в философском аспекте бывает, в основном: мировоззренческая; эстетическая; религиозная; научная; бытовая; техническая; экономическая; технологическая.

Все это (с человеком) составляет ноосферу общества - более высокое состояние биосферы, возникшее в результате эволюции, структурирования, упорядочивания и гармонизации связей в природе и обществе под воздействием целеполагающей деятельности человечества. Это понятие введено впервые В. И. Вернадским в качестве отражения эволюции общества и природы т.е. системы, в рамках которой потенциально может быть реализовано гармоническое, устойчивое развитие (эволюция) систем “Общество” и “Природа”, а также постепенное слияние, интеграция и гармонизация наук о природе, познании и об обществе. Без этого невозможно построение информационного общества.

Информация может оказаться и вредной, влияющей негативно на сознание, например, воспитывающей восприятие мира от безразличного или же некритического - до негативного, "обозлённого", неадекватного. Информационный поток - достаточно сильный раздражитель.

Пример. Негативной информацией - раздражителем может быть информация о крахе коммерческого банка, о резком росте (спаде) валютного курса, об изменении налоговой политики и др.

Информация не существует без других типов ресурсов - энергии, вещества, организации, как и они не могут существовать без информации. Любые взаимодействия систем (подсистем) - взаимодействия всегда материальноэнерго-информационные. Выявление (структурирование, упорядочивание, установление отношений), формализация (описание формальными средствами, языками), изучение (разработка моделей, методов, алгоритмов), применение (разработка и актуализация технологий) этих взаимодействий и составляет основную задачу информатики - как науки, как человеческой деятельности.

Если отвлечься от конкретного смыслового содержания информации и рассматривать сообщения информации как последовательности знаков, сигналов, то их можно представлять битами, а измерять в байтах, килобайтах, мегабайтах, гигабайтах, терабайтах и петабайтах.

Информация может пониматься и интерпретироваться по разному. Вследствие этого имеются различные подходы к определению методов измерения информации, меры количества информации. Раздел информатики (теории информации) изучающий методы измерения информации называется информметрией.

Количество информации - числовая величина, адекватно характеризующая актуализируемую информацию по разнообразию, сложности, структурированности, определённости, выбору (вероятности) состояний отображаемой системы.

Если рассматривается система, которая может принимать одно из n возможных состояний, то актуальна задача оценки такого выбора, исхода. Такой оценкой может стать мера информации (или события). Мера - это некоторая непрерывная действительная неотрицательная функция, определённая на множестве событий и являющаяся аддитивной т.е. мера конечного объединения событий (множеств) равна сумме мер каждого события.

1. Мера Р. Хартли. Пусть имеется N состояний системы S или N опытов с различными, равновозможными последовательными состояниями системы. Если каждое состояние системы закодировать, например, двоичными кодами определённой длины d, то эту длину необходимо выбрать так, чтобы число всех различных комбинаций было бы не меньше, чем N. Наименьшее число, при котором это возможно или мера разнообразия множества состояний системы задаётся формулой Р. Хартли: H=k log _а N, где k - коэффициент пропорциональности (масштабирования, в зависимости от выбранной единицы измерения меры), а - основание системы меры.

Если измерение ведётся в экспоненциальной системе, то k=1, H=lnN (нат); если измерение - в двоичной системе, то k=1/ln2, H=log₂N (бит); если измерение - в десятичной системе, то k=1/ln10, H=lgN (дит).

Пример. Чтобы узнать положение точки в системе из двух клеток т.е. получить некоторую информацию, необходимо задать 1 вопрос ("Левая или правая клетка?"). Узнав положение точки, мы увеличиваем суммарную информацию о системе на 1 бит (I=log₂ 2). Для системы из четырех клеток необходимо задать 2 аналогичных вопроса, а информация равна 2 битам (I=log₂4). Если система имеет n различных состояний, то максимальное количество информации равно I=log₂ n.

По Хартли, для того, чтобы мера информации имела практическую ценность - она должна быть такова, чтобы отражала количество информации пропорционально числу выборов.

Пример. Имеются 192 монеты из которых одна фальшивая. Определим сколько взвешиваний нужно произвести, чтобы определить ее. Если положить на весы равное количество монет, то получим 2 возможности (мы сейчас отвлекаемся от того, что в случае фальшивой монеты таких состояний будет два - состояния независимы): а) левая чашка ниже; б) правая чашка ниже. Таким образом, каждое взвешивание дает количество информации I=log₂2=1 и, следовательно, для определения фальшивой монеты нужно сделать не менее k взвешиваний, где k удовлетворяет условию log₂2k³ log₂

Похожие работы

Энтропия. Теория информации

Скачать

63729

48

3

... порядок чередования букв формируется согласно правилам, заданным верхними иерархическими уровнями текста, то есть не «снизу вверх», а «сверху вниз». Что же касается исполь­зуемой теорией информации вероятностной функции энтропии, то она может быть использована в качестве точного математического инструмента только на нижних уровнях иерархии текста, поскольку только на этих уровнях удается найти ...

Энтропия и ее роль в построении современной картины мира

Скачать

30658

0

0

... когда с момента возникновения новой парадигмы не прошло и ста лет многие ученые высказывают предположения о близости новых глобальных революционных изменений в научной картине мира. 2. Энтропия в современной картине мира   2.1 Синергетика В классической науке господствовало убеждение, что материи свойственна тенденции к понижению степени ее упорядоченности, стремление к равновесию, что ...

Энтропия термодинамическая и информационная

Скачать

18208

0

0

... числа микросостояний, посредством которых реализуется макросостояние. В состоянии равновесия энтропия достигает максимального значения, поскольку в равновесном состоянии термодинамическая вероятность максимальна. Отсюда следует, что энтропия изолированной предоставленной самой себе системы должна возрастать до тех пор, пока не достигнет максимального значения, совместимого с условиями. Следует ...

Энтропия сигналов

Скачать

11875

4

8

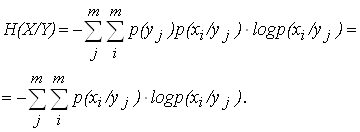
... 2. Таблица 2 Y X y1 y2 ym x1 x2 xm p(x1/y1) p(x1/y2) . . . p(x1/ym) p(x2/y1) p(x2/y2) . . . p(x2/ym) p(xm/y1) p(xm/y2) . . . p(xm/ym) Вероятности расположения на диагонали характеризует вероятность правильной передачи, остальные – ложной. Для равновероятных сигналов на входе приемника общая условная энтропия вычисляется по формуле: . (6) Для не равновероятных ...