Навигация
Теорема Шеннона о кодировании при наличии помех
3. Теорема Шеннона о кодировании при наличии помех
Рассмотрим первую теорему Шеннона. Первая теорема Шеннона о передаче информации, которая называется также основной теоремой о кодировании при отсутствии помех, формулируется следующим образом: при отсутствии помех передачи всегда возможен такой вариант кодирования сообщения, при котором среднее число знаков кода, приходящихся на один знак кодируемого алфавита, будет сколь угодно близко к отношению средних информаций на знак первичного и вторичного алфавитов.
Используя понятие избыточности кода, можно дать более короткую формулировку теоремы: при отсутствии помех передачи всегда возможен такой вариант кодирования сообщения, при котором избыточность кода будет сколь угодно близкой к нулю.
Данные утверждения являются теоремами и, следовательно, должны доказываться, однако доказательства мы опустим. Для нас важно, что теорема открывает принципиальную возможность оптимального кодирования. Однако необходимо сознавать, что из самой теоремы никоим образом не следует, как такое кодирование осуществить практически – для этого должны привлекаться какие-то дополнительные соображения, что и станет предметом нашего последующего обсуждения.
Далее в основном ограничим себя ситуацией, когда M = 2, т.е. для представления кодов в линии связи используется лишь два типа сигналов – с практической точки зрения это наиболее просто реализуемый вариант (например, существование напряжения в проводе (будем называть это импульсом) или его отсутствие (пауза); наличие или отсутствие отверстия на перфокарте или намагниченной области на дискете); подобное кодирование называется двоичным. Знаки двоичного алфавита принято обозначать "0" и "1", но нужно воспринимать их как буквы, а не цифры. Удобство двоичных кодов и в том, что при равных длительностях и вероятностях каждый элементарный сигнал (0 или 1) несет в себе 1 бит информации (log2M = 1); тогда из (1), теоремы Шеннона:
I1(A)![]() K(2)
K(2)
и первая теорема Шеннона получает следующую интерпретацию: при отсутствии помех передачи средняя длина двоичного кода может быть сколь угодно близкой к средней информации, приходящейся на знак первичного алфавита.
Применение формулы (2) для двоичного кодирования дает:
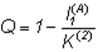
Определение количества переданной информации при двоичном кодировании сводится к простому подсчету числа импульсов (единиц) и пауз (нулей). При этом возникает проблема выделения из потока сигналов (последовательности импульсов и пауз) отдельных кодов. Приемное устройство фиксирует интенсивность и длительность сигналов. Элементарные сигналы (0 и 1) могут иметь одинаковые или разные длительности. Их количество в коде (длина кодовой цепочки), который ставится в соответствие знаку первичного алфавита, также может быть одинаковым (в этом случае код называется равномерным) или разным (неравномерный код). Наконец, коды могут строиться для каждого знака исходного алфавита (алфавитное кодирование) или для их комбинаций (кодирование блоков, слов). В результате при кодировании (алфавитном и словесном) возможны следующие варианты сочетаний:
Таблица 1.
| Варианты сочетаний длительности элементарных сигналов | Кодировка первичных символов (слов) | Ситуация |
| одинаковые | равномерная | (1) |
| одинаковые | неравномерная | (2) |
| разные | равномерная | (3) |
| разные | неравномерная | (4) |
В случае использования неравномерного кодирования или сигналов разной длительности (ситуации (2), (3) и (4)) для отделения кода одного знака от другого между ними необходимо передавать специальный сигнал – временной разделитель (признак конца знака) или применять такие коды, которые оказываются уникальными, т.е. несовпадающими с частями других кодов. При равномерном кодировании одинаковыми по длительности сигналами (ситуация (1)) передачи специального разделителя не требуется, поскольку отделение одного кода от другого производится по общей длительности, которая для всех кодов оказывается одинаковой (или одинаковому числу бит при хранении).
Длительность двоичного элементарного импульса (![]() ) показывает, сколько времени требуется для передачи 1 бит информации. Очевидно, для передачи информации, в среднем приходящейся на знак первичного алфавита, необходимо время
) показывает, сколько времени требуется для передачи 1 бит информации. Очевидно, для передачи информации, в среднем приходящейся на знак первичного алфавита, необходимо время ![]() . Таким образом, задачу оптимизации кодирования можно сформулировать в иных терминах: построить такую систему кодирования, чтобы суммарная длительность кодов при передаче (или суммарное число кодов при хранении) данного сообщения была бы наименьшей.
. Таким образом, задачу оптимизации кодирования можно сформулировать в иных терминах: построить такую систему кодирования, чтобы суммарная длительность кодов при передаче (или суммарное число кодов при хранении) данного сообщения была бы наименьшей.
§4. Пример использования энтропии в прогнозировании и ее значение для прогнозирования. Применение к рискам
Прогнозирование — частный вид моделирования как основы познания и управления.
Роль прогнозирования в управлении страной, отраслью, регионом, предприятием очевидна. Необходимы учет СТЗП-факторов (социальных, технологических, экономических, политических), факторов конкурентного окружения и научно-технического прогресса, а также прогнозирование расходов и доходов предприятий и общества в целом (в соответствии с жизненным циклом продукции — во времени и по 11-ти стадиям международного стандарта ИСО 9004). Проблемы внедрения и практического использования математических методов эконометрического прогнозирования связаны прежде всего с отсутствием в нашей стране достаточно обширного опыта подобных исследований, поскольку в течение десятилетий планированию отдавался приоритет перед прогнозированием.
В конкретных задачах прогнозирования необходимо провести классификацию рисков, поставить задачу оценивания конкретного риска, провести структуризацию риска. Риски необходимо учитывать при прогнозировании экономических последствий принимаемых решений, поведения потребителей и конкурентного окружения, внешнеэкономических условий и макроэкономического развития России, экологического состояния окружающей среды, безопасности технологий, экологической опасности промышленных и иных объектов.
Большое число рисков связано с природными явлениями. Их можно объединить под именем «экологические». К ним относятся, в частности риски, связанные с неопределенностью ряда природных явлений. Типичным примером является погода, от которой зависят урожайность (а потому и цены на сельскохозяйственные товары), расходы на отопление и уборку улиц, доходы от туризма и др. Особое значение имеют риски, связанные с недостаточными знаниями о природе (например, неизвестен точный объем полезных ископаемых в том или ином месторождении, а потому нельзя точно предсказать развитие добывающей промышленности и объем налоговых поступлений от ее предприятий). Нельзя забывать о рисках экологических бедствий; и катастроф типа ураганов, смерчей, землетрясений, цунами, селей и др.
В настоящее время при компьютерном и математическом моделировании для описания неопределенностей все чаще используют такой метод, как энтропия. Некоторые виды неопределенностей связаны с безразличными к организации силами — природными (погодные условия) или общественными (смена правительства).
Разнообразные формальные методы оценки рисков и управления ими во многих случаях (реально во всех нетривиальных ситуациях) не могут дать однозначных рекомендаций. В конце процесса принятия решения — всегда человек, менеджер, на котором лежит ответственность за принятое решение.
Поэтому процедуры энтропии естественно применять не только на конечном, но и на всех остальных этапах анализа рассматриваемого организацией проекта, используя при этом весь арсенал теории и практики энтропии.
Рассмотрим использования энтропии на примере прогноза погоды.
Пусть для некоторого пункта вероятность того, что 15 июня будет идти дождь, равна 0,4, а вероятность того, что дождя не будет, равна 0,6. Пусть далее для этого же пункта вероятность дождя 15 октября равна 0,8, а вероятность отсутствия дождя в этот день — всего 0,2. Предположим, что определенный метод прогноза погоды 15 июня оказывается правильным в 3/5 всех тех случаев, в которых предсказывается дождь, и в 4/5 тех случаев, в которых предсказывается отсутствие осадков; в применении же к погоде 15 октября этот метод оказывается правильным в 9/10 тех случаев, в которых предсказывается дождь, и в половине случаев, в которых предсказывается отсутствие дождя (сравнительно большой процент ошибок в последнем случае естественно объясняется тем, что предсказывается маловероятное событие, предугадать которое довольно трудно). Спрашивается, в какой из двух указанных дней прогноз дает нам больше информации о реальной погоде?
Обозначим через β1 и β2 опыты, состоящие в определении погоды в рассматриваемом пункте 15 июня и 15 октября. Мы считаем, что эти опыты имеют всего по два исхода — В (дождь) и ![]() (отсутствие осадков); соответствующие таблицы вероятностей имеют вид:
(отсутствие осадков); соответствующие таблицы вероятностей имеют вид:
Опыт β1
| исходы | В |
|
| вероятн. | 0,4 | 0,6 |
Опыт β2
| исходы | В |
|
| вероятн. | 0,8 | 0,2 |
Следовательно, энтропии опытов β1 и β2 равны
Н (β1 ) = -0,4 log 0,4 — 0,6 log 0,6 ![]() 0,97 бита,
0,97 бита,
Н (β2) = - 0,8 log 0,8 - 0,2 log 0,2 ![]() 0,72 бита.
0,72 бита.
Пусть теперь α1 и α2 — предсказания погоды на 15 июня и на 15 октября. Опыты α1 и α2 также имеют по два исхода: А (предсказание дождя) и ![]() (предсказание сухой погоды); при этом пары опытов (α1, β1)и (α2,β2) характеризуются следующими таблицами условных вероятностей:
(предсказание сухой погоды); при этом пары опытов (α1, β1)и (α2,β2) характеризуются следующими таблицами условных вероятностей:
Пара (α1, β1)
|
|
|
|
|
| 0,6 | 0,4 | 0,2 | 0,8 |
Пара (α2,β2)
|
|
|
|
|
| 0,9 | 0,1 | 0,5 | 0,5 |
(![]() ). Эти таблицы позволяют определить также и неизвестные нам вероятности р1(А) и р1(
). Эти таблицы позволяют определить также и неизвестные нам вероятности р1(А) и р1(![]() ),р2(А) и р2(
),р2(А) и р2(![]() ) исходов А и
) исходов А и ![]() опытов α1 и α2. По формуле полной вероятности имеем для опыта β1
опытов α1 и α2. По формуле полной вероятности имеем для опыта β1
0,4=р(В)= р1(А) ![]() + р1(
+ р1(![]() )
)![]() =0,6· р1(А)
+0,2· р1(
=0,6· р1(А)
+0,2· р1(![]() )
)
и для опыта β2
0,8 = р (В)= р2(А) ![]() + р2(
+ р2(![]() )
)![]() =0,9· р2(А)+0,5· р2(
=0,9· р2(А)+0,5· р2(![]() ).
).
Так как р1(![]() )= 1 — р1(А), р2(
)= 1 — р1(А), р2(![]() )= 1 — р2(А), то отсюда получаем
)= 1 — р2(А), то отсюда получаем
р1(А)= р1(![]() )= 0,5, р2(А)
= 0,75, р2(
)= 0,5, р2(А)
= 0,75, р2(![]() ) = 0,25.
) = 0,25.
Подсчитаем теперь энтропии НА(β1), ![]() (в битах):
(в битах):
НА(β1)= -0,6• log 0,6 - 0,4 • log 0,4 ![]() 0,97,
0,97,
![]() = - 0,2• log 0,2 – 0,8• log0,8
= - 0,2• log 0,2 – 0,8• log0,8 ![]() 0,72
0,72
и
![]() = - 0,9 • log 0,9 - 0,1• log 0,1
= - 0,9 • log 0,9 - 0,1• log 0,1![]() 0,47,
0,47,
![]() = - 0,5 • log 0,5 - 0,5• log 0,5= 1.
= - 0,5 • log 0,5 - 0,5• log 0,5= 1.
Следовательно,
![]() р1(А) НА(β1)+ р1(
р1(А) НА(β1)+ р1(![]() )
)![]()
![]() 0,84,
0,84,
![]() р2(А)
р2(А) ![]() + р2(
+ р2(![]() )
)![]()
![]() 0,60.
0,60.
Таким образом, информация, содержащаяся в прогнозе погоды на 15 июня (опыт α1) о реальной погоде в этот день (об опыте β2), равна
I (α1, β1) = Н(β1)- ![]()
![]() 0,97 -0,84 = 0,13 бит,
0,97 -0,84 = 0,13 бит,
что несколько больше, чем информация о реальной погоде 15 октября (об опыте β2), содержащаяся в прогнозе погоды на этот день (в опыте α2):
I (α2, β2) = Н(β2)- ![]()
![]() 0,72 — 0,60 = 0,12 бит.
0,72 — 0,60 = 0,12 бит.
Этот результат позволяет считать прогноз погоды па 15 нюня более ценным, чем прогноз на 15 октября, несмотря на то, что последний прогноз чаще оказывается правильным: действительно, в силу формулы полной вероятности, для прогноза погоды на 15 нюня вероятность оказаться правильным равна
р1(А)
![]() + р1(
+ р1(![]() )
)![]() = 0,5• 0,6 + 0,5• 0,8 = 0,7,
= 0,5• 0,6 + 0,5• 0,8 = 0,7,
в то время как для прогноза погоды на 15 октября эта вероятность равна
р2(А) ![]() + р2(
+ р2(![]() )
)![]() = 0,75 • 0,9 + 0,25 • 0,5 = 0,8.
= 0,75 • 0,9 + 0,25 • 0,5 = 0,8.
Заключение
Энтропия как физическая переменная первично возникла из задач описания тепловых процессов. Впоследствии она стала широко использоваться во всех областях науки.
Информация - это знание, которое используется для развития, совершенствования системы и её взаимодействий с окружающей средой.
Информация сама развивается вслед за развитием системы. Новые формы, принципы, подсистемы, взаимосвязи и отношения вызывают изменения в информации, ее содержании, формах получения, переработки, передачи и использования. Благодаря потокам информации система осуществляет целесообразное взаимодействие с окружающей средой, т.е. управляет или управляема. Своевременная и оперативная информация может позволить стабилизировать систему, адаптироваться, восстанавливаться при нарушениях структуры и/или подсистем. От степени информированности системы, от взаимодействия системы и среды зависит развитие и устойчивость системы.
В современном мире все большее значение в управлении организацией отдается прогнозированию. Любая организация в процессе своей деятельности сталкивается с различными рисками, которые в большей или меньшей степени влияют на ее состояние. Многочислелны примеры ситуаций, связанных с социальными, технологическими, экономическими, политическими, экологическими и другими рисками. Именно в таких ситуациях обычно и необходимо прогнозирование. Известны различные виды критериев, используемых в теории принятия решений в условиях неопределенности (риска). Из-за противоречивости решений, получаемых по различным критериям, очевидна необходимость применения энтропии.
Список используемой литературы
1. Дмитриев В.Н. Прикладная теория информации. М: Высшая школа,1989.
2. Колмогоров А.Н. Теория информации и теория алгоритмов.М:Наука,1987.
3. Колмогоров А.Н. Три подхода к определению понятия “количество информации” // Проблемы передачи информации. 1965. Т.1. №1.
4. Поплавский Р.П. Депон Максвелла и соотношения между информацией и энтропией // УФН. 1979. Т. 128. Вып. 1.
5. Хартли Р. Передача информации// Теория информации и ее приложения. М.: Физматгиз. 1959.
6. Шамбадаль П. Развитие и приложения понятия энтропии . М.: Наука, 1967 .
7. Яглом А.М., Яглом И.М. Вероятность и информация. М.: Наука, 1973.
Похожие работы
... порядок чередования букв формируется согласно правилам, заданным верхними иерархическими уровнями текста, то есть не «снизу вверх», а «сверху вниз». Что же касается используемой теорией информации вероятностной функции энтропии, то она может быть использована в качестве точного математического инструмента только на нижних уровнях иерархии текста, поскольку только на этих уровнях удается найти ...
... когда с момента возникновения новой парадигмы не прошло и ста лет многие ученые высказывают предположения о близости новых глобальных революционных изменений в научной картине мира. 2. Энтропия в современной картине мира 2.1 Синергетика В классической науке господствовало убеждение, что материи свойственна тенденции к понижению степени ее упорядоченности, стремление к равновесию, что ...
... числа микросостояний, посредством которых реализуется макросостояние. В состоянии равновесия энтропия достигает максимального значения, поскольку в равновесном состоянии термодинамическая вероятность максимальна. Отсюда следует, что энтропия изолированной предоставленной самой себе системы должна возрастать до тех пор, пока не достигнет максимального значения, совместимого с условиями. Следует ...
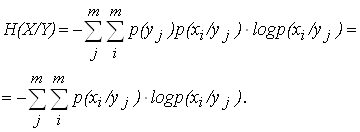
... 2. Таблица 2 Y X y1 y2 ym x1 x2 xm p(x1/y1) p(x1/y2) . . . p(x1/ym) p(x2/y1) p(x2/y2) . . . p(x2/ym) p(xm/y1) p(xm/y2) . . . p(xm/ym) Вероятности расположения на диагонали характеризует вероятность правильной передачи, остальные – ложной. Для равновероятных сигналов на входе приемника общая условная энтропия вычисляется по формуле: . (6) Для не равновероятных ...


0 комментариев