Навигация
3. РАСЧЕТ ЗУБЧАТЫХ ПЕРЕДАЧ
3.1. Выбор материалов и допускаемых напряжений
Так как крутящий момент ведомого вала равняется Т2=140[Нм], то целесообразнее всего цементация стали.
Для изготовления зубчатых колес выбираем сталь марки 25ХГТ. После термообработки, твердость шестерни составит около 610 НВ, а твердость колеса - около 570 НВ.
Допускаемые контактные напряжения:
![]() ; (3.1)
; (3.1)
где: ![]() - базовый предел контактной выносливости;
- базовый предел контактной выносливости;
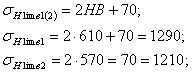 |
При улучшении формула определения базового предела контактной выносливости примет вид (3.2):
SH - коэффициент запаса, принятый равным для цементации + закалки SH=1,2;
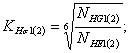 (3.3)
(3.3)
![]() - коэффициент долговечности.
- коэффициент долговечности.
Однако следует учесть, что формула (3.3) работает только когда NHE>NHG. В противном случае следует принять ![]()
где: NHG1(2)- базовое число циклов предела контактной выносливости, определяемое по графикам, изображенным на рис. 3.
По графику определяем: NHG1=140*106
NHG2=130*106
NHE1(2)- эквивалентное число циклов нагружения шестерни и колеса, рассчитываемое по формуле:
![]() (3.4)
(3.4)
где: L = 16 тыс. ч. - срок службы, приведенный в задании;
kmax,ki,li- относительные величины нагрузок и относительная продолжительность
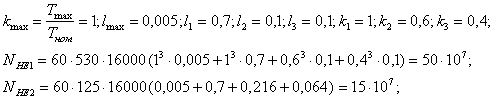 |
их действия, приведенные в задании на курсовое проектирование и циклограмме нагрузки:
Так как NHE1>NHG1,то ![]()
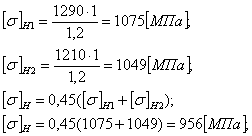 |
Так как NHE2>NHG2 ,то
Определим допускаемые напряжения изгиба:
![]() базовый предел изгибной выносливости, равный для улучшения: (3.5)
базовый предел изгибной выносливости, равный для улучшения: (3.5)
 |
Коэффициент запаса SF для цементации + закалки:
SF =1,5.
Коэффициент долговечности при закалке:
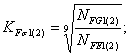 (3.6)
(3.6)
Однако следует учесть, что формула (3.3) работает только когда NFE>-NFG. В противном случае следует принять ![]() =1.
=1.
NFG1(2) - базовое число циклов. Примем NFG1(2) = 4*106.
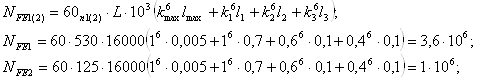 (3.8)
(3.8)
Так как ![]() , то принимаем
, то принимаем ![]() ;
;
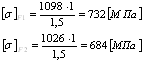
![]() (3.9)
(3.9)
Примем ![]() = 0,255 .
= 0,255 .
Тогда получим значение межосевого расстояния, округленное до стандартного:
![]() (3.10)
(3.10)
Назначим модуль зацепления: mn=0.018*aw=1,3; Выберем стандартный модуль зацепления m=2.5 Определим суммарное число зубьев шестерни и колеса:
![]() (3.11)
(3.11)
где: ![]() может принять значение в диапазоне от 0,86 до 0,88. Примем:
может принять значение в диапазоне от 0,86 до 0,88. Примем: ![]() ' = 0,87;
' = 0,87;
![]() Округлим
Округлим ![]() до целого значения, получив при этом
до целого значения, получив при этом ![]() =97. Далее уточним значение угла наклона зубьев:
=97. Далее уточним значение угла наклона зубьев:
![]() , откуда:
, откуда:![]() .
.
Определим число зубьев шестерни:
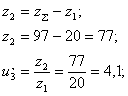 |
Тогда:
Проверим верность расчета:
![]()
![]() (3.13)
(3.13)
Выполнение условия (3.15) свидетельствует о верности расчета.
Основные параметры зубчатых колес
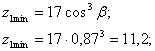 |
Минимальное число зубьев, которое можно нарезать без смещения:
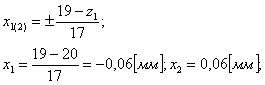 |
Так как
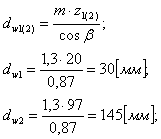 |
Начальные (делительные) диаметры зубчатых колес:
Диаметры окружностей выступов:
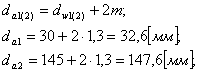 (3.14)
(3.14)
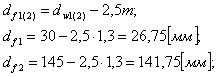 |
Диаметры окружностей впадин:
![]()
Ширина колес должна удовлетворять условию ![]() , примем b = 20 (мм), что соответствует условию.
, примем b = 20 (мм), что соответствует условию.
Линейная скорость:
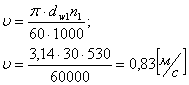 (3.15)
(3.15)
По таблице П. 14 [1, стр. 73], выбираем точности изготовления колес, в зависимости от линейной скорости. Как видно, для их изготовления достаточна восьмая (средняя) степень точности.
Определяем силу в зацеплении
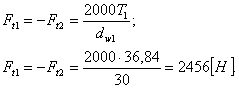 |
Окружные силы:
Радиальные силы:
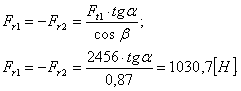 |
Осевые силы:
- коэффициент, учитывающий форму сопрягаемых поверхностей
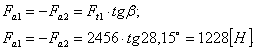 |
3.3. Проверочный расчет зубчатых передач
![]()
Определяем фактические контактные напряжения:
z„ = 1,76^0,973 =1,733;
Коэффициент, учитывающий перекрытие: Т
zi =
sa - коэффициент торцевого перекрытия, который равен:
Коэффициент неравномерности распределения нагрузки по ширине зуба определяем по рисунку 4.2 [1, стр. 20]: к1ф = 1,3.
Коэффициент динамической нагрузки определяем из таблицы П.16 [1, стр.74]: ^,=1,02.
Теперь можем подставить значения всех найденных коэффициентов и выполнить проверку неравенства:
Далее определяем фактические напряжения изгиба для более слабых зубьев. Эквивалентное число зубьев прямозубых колес:
Теперь по рисунку 4.3 [1, стр. 21] определяем коэффициенты формы зубьев зубчатых колес YF];YF2, в зависимости от значений zvl;zv2. Итак, получили:
Ул(х = 0,006;г = 21)*4.15;
FF2(x = -0.006;z = 9l)*3,72.
Расчет фактического напряжения изгиба ведем для колеса, у которого отношение окажется меньше:
Как видно, расчет будем вести для шестерни: FY к к Y
Коэффициент неравномерности распределения нагрузки по ширине зуба определяем по рисунку 4.2 [1, стр. 20]: kFp = 1,3.
Коэффициент динамической нагрузки определяем из таблицы П. 16 [1, стр. 74]:
*,у=1,09.
Коэффициент, учитывающий наклон зубьев:
Теперь можем подставить значения всех найденных коэффициентов и выполнить проверку неравенства:
Выполнение условий проверочного расчета зубчатой передачи свидетельствует о верности выполнения основного расчета.
Похожие работы
... – через сливное отверстие, уровень масла показывается с помощью маслоуказателя. Смазка подшипников осуществляется тем же маслом что и зубчатые колеса путем разбрызгиванием масла. Заключение При выполнении данной курсовой работы рассчитан привод и спроектирован редуктор привода. При расчёте двухступенчатого редуктора мы выбрали двигатель 4А132S4У3, у которого мощность , частота вращения .
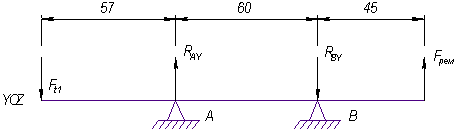
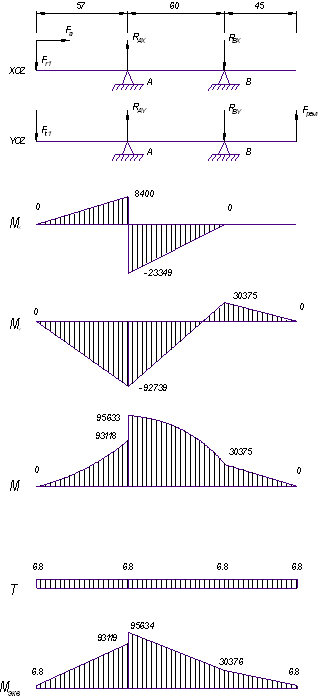
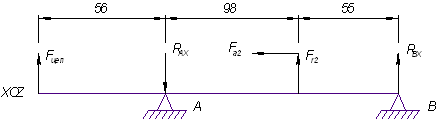
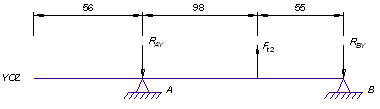
... 12,4-14,5 мм. Назначаем dк = 25 мм. dбк ≥ 25+3 ּ 1 = 28 мм. Назначаем dбк = 28 мм. dп = 25-3 ּ 1,5 = 21,5 мм. Назначаем dп = 20 мм. dбп ≥ 20+3 ּ 1,5 = 24,5 мм. Назначаем dбп = 25 мм. 3.2.3 Проверочный расчет валов Плоскость YOZ (вертикальная). Для определения реакции Rb воспользуемся уравнением (3.4) - Fr1 ּ 28+Fa2 ּ 45+Fr2 ּ 39+Fa1 &# ...
... . Наиболее полно требования снижения массы и габаритных размеров удовлетворяет привод с использованием электродвигателя и редуктора с внешним зацеплением. 1. Энергетический и кинематический расчет привода Мощность, потребляемую конвейером, по ф. стр.5 [1]: Pp=FtV= 4×103×1,6=6,4 кВт, где Ft– тяговое усилие на барабане, кН; V – окружная скорость Мощность, потребляемая ...
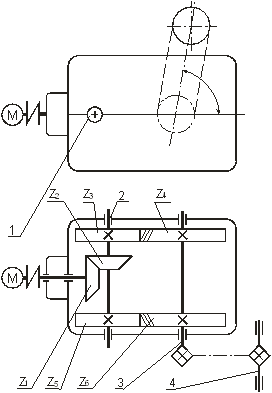
... и отдельных элементов привода [Л1] (табл. 1.2.1). Для нашего привода (рис.1): Рисунок 1 – Схема привода: 1 – электродвигатель, 2 – ременная передача, 3 – редуктор конический одноступенчатый, 4 – цепная передача. Расчетная мощность электродвигателя, кВт: ; (1.2) На основании рекомендуемых min и max величин передаточных чисел u для ...
0 комментариев