Навигация
1.6. Выводы
Нами была исследована различная методическая литература. Многие авторы ведут свой разговор о методике обучения решению задач, большинство выделяет основные этапы данной работы (Бантова М.А., Истомина И.Б., Царева С.Е. и т.д.). Много внимания уделяется этапам анализа текста, поиску и оформлению решения. Последний этап в работе над задачей – работа после решения задачи – в методической литературе встречается достаточно часто, авторами предлагаются различные виды упражнений на данном этапе. На практике можно увидеть эффективность этих видов работы. К сожалению учителя зачастую не используют подобные задания, а если и используют, то мало, причиной этому является недостаток учебного времени и отсутствие методики по данному вопросу.
Рассмотрев статьи учителей в журналах «Начальная школа», «Математика в школе» и т. п. мы сделали вывод, что учителя часто сталкиваются с проблемой повышения уровня умения решать задачи, они нуждаются в дополнительных заданиях и подробной методике их проведения. Некоторые учителя делали попытку в разработке подобных методик, так Шорникова И.В. в журнале «Начальная школа» [38, с. 21] предлагает несколько видов работ по преобразованию задач, но методику обучения преобразованию задач все же не освещает.
Так как вопрос методики обучения преобразованию задач освещен в наименьшей степени, мы продолжим его изучение.
Глава II. Методика обучения преобразованию задач.
2.1. Преобразования задачи на уроках математики в начальной школе.
Так как специализированной литературы, касающейся преобразования задач очень мало, то мы решили провести анкетирование среди учителей начальной школы с целью проверки их просвещенности по данному вопросу и выяснения места данной работы на уроках математики в начальной школе.
В анкетировании участвовало 10 респондентов, которым предлагалось ответить на следующие вопросы:
1. Как вы понимаете понятие «Преобразование задач»?
2. Имеет ли место работа по преобразованию задач на уроках математики в вашем классе?
3. Если вы ответили «да» на вопрос №2, то выберите одно из следующих утверждений, отражающее наиболее подходящие данные:
а) я веду данную работу на каждом уроке;
б) я провожу данную работу раз в неделю;
в) я провожу данную работу более одного раза в месяц;
г) я провожу данную работу раз в год;
д) я провожу данную работу по мере появления данных заданий в учебнике.
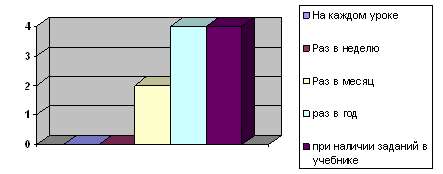
Результаты анкетирования показали, что понятие «Преобразование задач» понимается всеми респондентами как изменение условия, вопроса задачи, но к тому же один человек из них отнес к данному виду работ составление обратных задач, другой - изменение данных задачи. Все респонденты проводят подобную работу на своих уроках, но не так часто как хотелось бы. Ни один учитель не проводит работу по преобразованию задач на каждом уроке, или раз в неделю. Но 2 респондента ответили, что проводят данную работу раз в месяц, 4 человека используют такой вид работы раз в год и 4 человека ответили, что применяют подобные задания только при наличии их в учебнике.
Нами были рассмотрены учебники 2 и 3 классов по разным программам.
| Автор программы | 2 класс | 3 класс | ||
| Количество задач | Количество заданий по преобразованию задач | Количество задач | Количество заданий по преобразованию задач | |
| Моро М.И., Бантова М.А., Бельтюкова Г.Б. | 296 | 16 | 311 | 5 |
| Истомина Н.Б., Нефедова И.Б. | 196 | 2 | 224 | 5 |
| Рудницкая В.Н., Юдачева Т.В. | 350 | 19 | 151 | 0 |
| Демидова Т.Е. Козлова С.А. Тонких А.П. | 188 | 9 | 382 | 7 |
Таким образом, было выявлено, что во всех рассмотренных нами программах количество заданий по преобразованию задач минимальное. Поэтому мы рекомендуем учителям использовать дополнительные задания, вести работу над задачей после ее решения.
Исследовав методическую литературу, прочитав труды многих авторов, мы установили то, что все методисты включают работу по преобразованию задач в этап работы над задачей после ее решения, но ни один методист не освещает вопрос о методике обучения преобразованию задач. Это привело нас к тому, что мы решили попробовать разработать методику обучения преобразованию задач и реализовать ее на уроках математики в начальной школе.
Исследование проводилось на базе 2 «в» класса 48 школы. В исследовании принимали участие 18 учеников.
Цель исследования: апробировать на практике разработанную нами методику обучения преобразованию задач.
Задачи:
1. Выяснить с помощью срезовой контрольной работы уровень умения решать задачи каждого ученика;
2. Выяснить с помощью контрольной работы умение детей преобразовывать задачи;
3. Разработать и провести ряд уроков с целью обучения детей преобразованию задач;
4. Выяснить с помощью срезовой контрольной работы уровень умения решать задачи каждого ученика;
5. Выяснить с помощью контрольной работы умение детей преобразовывать задачи;
6. Выяснить с помощью контрольной работы, на сколько дети усвоили понятие «преобразовать задачу»;
7. Сделать выводы по проделанной работе и полученным результатам.
Разработанная нами методика обучения преобразованию задач состоит из трех этапов: подготовительная работа, обучение преобразованию задач и закрепление.
2.2. Подготовительная работа.
На первой ступени обучения преобразованию задач должна быть создана у учащихся готовность к работе над задачей после ее решения: они должны обобщить знание тех связей, на основе которых выбираются арифметические действия, знание объектов и жизненных ситуаций, о которых говорится в задаче, и собственно уметь решать задачи.
Кроме того, при работе на первом этапе учащиеся должны вспомнить и активно использовать понятия и термины, относящиеся к самой задаче и ее решению (задача, условие задачи, вопрос или требование задачи, решение задачи, ответ на вопрос задачи).
Для решения составных задач ученики должны уметь вычленять систему связей, т.е. разбивать составную задачу на простые.
Урок на тему «Решение задач» был вызван необходимостью повторения структурных компонентов задачи, повторения этапов и общих приемов работы над задачей.
На данном этапе можно использовать следующие задания:
1.Разбор задачи
Цель: повторить общие приемы работы над задачей, актуализировать знания детей о структурных компонентах задачи
Например, детям предложена следующая задача: «В музей на экскурсию пришли 2 группы ребят по 9 человек в каждой. Сколько было ребят из первого класса, если из группы продленного дня было 8 человек?»
Так детям необходимо прочитать задачу и ответить на следующие вопросы: о чем говорится в задаче? Что нам известно? Какой вопрос ставится в задаче? Можем ли мы сразу на него ответить? Что нам для этого нужно найти? Из скольки простых задач состоит данная задача? С помощью какого действия мы решим первую простую задачу? С помощью какого действия мы решим вторую простую задачу?
Далее проходит работа по выделению в задаче условия, требования и связей между ними: - назовите условие задачи; - назовите требование, которое ставится в задаче; - какие слова указывают на выбор арифметического действия?
Затем составляется следующая краткая запись:
После этого дети оформляют в тетради решение задачи.
2.Постановка вопроса к условию задачи.
Цель: обобщить знания о связях между данными и искомым.
Детям предлагается разбиться на группы. Каждая группа выполняет следующее задание: подобрать к условию соответствующий вопрос. Учащиеся устанавливают, что можно узнать по определенным данным.
Например, даны условия задач: 1. В саду росло 3 яблони, 5 груш, а слив на 7 деревьев больше, чем яблонь и груш вместе; 2. В саду росло 25 деревьев, из них 7 были яблони и столько же груш; 3. В саду росло 2 ряда грушевых деревьев по 5 в каждом, и 1 ряд яблонь, состоящий из 6 деревьев. Из-за вредоносных насекомых пришлось срубить 8 деревьев.
Учащиеся могут предложить следующие вопросы: 1. Сколько вишен росло в саду? 2. Сколько всего деревьев в саду? 3. Сколько деревьев осталось в саду?
3.Составление условия задачи по данному вопросу.
Цель: обобщить знания о связях между данными и искомым.
При выполнении таких упражнений учащиеся устанавливают, какие данные надо иметь, чтобы найти искомое.
Например, учащимся предлагается составить условие задачи к вопросу: «Сколько ведер воды в двух бочках?». Дети устанавливают, что в условии может быть дано число ведер воды в каждой бочке или число ведер воды в одной из бочек и разность или отношение между числом ведер в первой и второй бочках и т.п.
На данном этапе обучения преобразованию задач необходимо подвести итог: чтобы решить задачу необходимо выделить следующие этапы, которые оформляются в памятку:
1. Прочитай внимательно задачу, найди в ней условие и вопрос.
2. Подумай, что обозначает в задаче каждое число.
3. Запиши кратко ее условие, начерти к ней схему или сделай рисунок.
4. Повтори задачу по краткой записи.
5. Подумай, что тебе уже известно и что еще надо найти.
6. Составь план решения задачи.
7. Запиши решение задачи.
8. Перечитай вопрос.
9. Запиши полный ответ.
Вся подготовительная работа сводится к выполнению учениками специальных упражнений, помогающих усвоить, актуализировать значение связей между числовыми данными в условии и между числовыми данными условия и требования.
Похожие работы
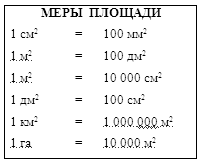
... и обобщение опыта учителей при проведении уроков математики по данной теме. Курсовая работа состоит из введения, двух глав, заключения, списка литературы. Глава I. Методические особенности изучения площади геометрических фигур и единиц ее измерения на уроках математики в начальной школе 1.1 Возрастные особенности развития младших школьников на этапе формирования геометрических представлений ...
... интересует. Соблюдение принципа наглядности – одно из основных требований, которому должно удовлетворять обучение математике в начальных классах. В начальных классах эффективно использовать технические средства обучения (ТСО) и наглядность по несколько минут на различных этапах урока. В процессе работы важно применять технические средства обучения в комплексе с другими средствами наглядности, ...
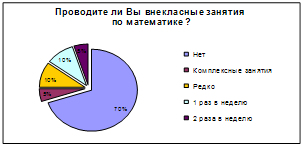
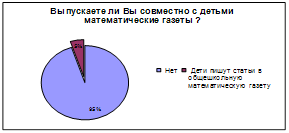
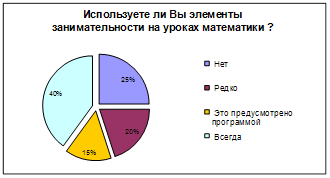
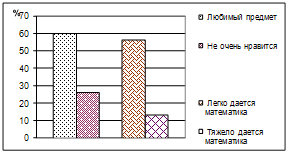
... и младших школьников. Анкета для студентов включала в себя два вопроса, один из которых о том, в чем, по их мнению, заключается развитие математических способностей школьников, а второй ¾ для выяснения отношения студентов к проведению внеклассной работы по математике в начальных классах. Анкета для преподавателей имела своей целью выяснить, проводят ли (а если проводят, то как часто) учителя ...
... натурального ряда. В качестве графической модели используем числовой луч, на котором дети отмечают точки, соответствующие натуральным числам. Смысл действий сложения и вычитания. В курсе математики начальной школы находит отражение теоретико-множественный подход к истолкованию сложения и вычитания целых неотрицательных чисел, в соответствии с которым сложение связано с операцией объединения, ...

0 комментариев