Навигация
3. Сопоставление задач.
Цель: показать важность отношений «больше на…», «больше в…», «меньше на…», и т.п.
На данном этапе полезно сопоставлять аналогичные задачи в два действия и видоизменять первую по образцу второй, а вторую по образцу первой. Например:
1) Мальчик успел решить на уроке 3 столбика примеров, по 4 примера в каждом столбике, а его сосед на 3 примера меньше. Сколько примеров решил второй мальчик?
2) В одном доме 3 этажа и в каждом этаже по 6 окон, а в другом доме на 2 окна больше. Сколько окон во втором доме?
При сопоставлении этих задач сначала указывается их сходство, затем разница и, наконец, выясняется, почему в задаче про мальчиков второе действие – вычитание, а в задаче про окна – сложение и как можно изменить первую задачу, чтобы она решалась как вторая и вторую, чтобы она решалась как первая.
4. Преобразование задачи
Цель: формировать у детей умение преобразовывать задачи на репродуктивном уровне, закрепить знания детей о компонентах задачи: условии и вопросе, закреплять знания и способы учебной деятельности при решении задач.
1) Детям дается задача: «В зоомагазине 4 клетки. В трех из них по 5 волнистых попугайчиков в каждой. Сколько волнистых попугайчиков в четвертой клетке, если в четырех клетках всего 22 волнистых попугайчика?»
- О чем говориться в задаче?
- Что нам известно?
- Какой вопрос ставится в задаче?
- Можем ли мы сразу на него ответить?
Составление краткой записи в виде предметной иллюстрации:




Решение задачи. Оформление решения.
Далее, работая над имеющейся краткой записью, изменяем задачу.
- «В зоомагазине 4 клетки. В двух из них по 5 волнистых попугайчиков в каждой. Сколько всего волнистых попугайчиков, если в двух других по 4 волнистых попугайчика в каждом?»
- Как изменится краткая запись?
- Что изменилось в задаче?
- Повторите новую задачу, опираясь на краткую запись.
- Решите эту задачу.
Задача № 4 стр.52 (Т.Е. Демидова, С.А. Козлова. Моя математика. 2 часть)
«В школьном уголке природы 4 аквариума. В трёх из них по 8 рыбок в каждом. Сколько рыбок в четвертом аквариуме, если в четырех аквариумах всего 31 рыбка?»
- О чем говориться в задаче?
- Что нам известно?
- Что значит по 8 рыбок в каждом?
- Какой вопрос ставится в задаче?
- Можем ли мы сразу на него ответить?
- Что нам нужно найти сначала?
- Сделаем краткую запись в виде рисунка:




- Решите задачу самостоятельно.
8 * 3 = 24 (р) в 3-х аквариумах 31 – 24 = 7(р) в 4-ом аквариуме
- Как мы можем изменить задачу? Составьте новую задачу, запишите ее и затем решите.
2) Задача № 5 стр. 57 (Т.Е. Демидова, С.А. Козлова. Моя математика. 2 класс, 2 часть): «Большой кенгуру сделал 3 прыжка по 8 метров, а затем в обратную сторону 2 прыжка по 9 метров. Какое расстояние преодолел кенгуру?»
- О чем говориться в задаче?
- Что нам известно?
- Какой вопрос ставится в задаче?
- Сделаем краткую запись.
- Можем ли мы сразу ответить на вопрос?
- Что нам нужно найти сначала?
8 * 3 = 24 (м) вперед 9 * 2 = 18 (м) назад 24 + 18 = 42 (м) всего
- Изменится ли задача, если я напишу её вот так: «Большой кенгуру пропрыгал 24 м вперед и 18 м назад. Какое расстояние преодолел кенгуру?»
- Какая часть задачи изменилась? Изменился ли вопрос?
- Изменится ли задача, если я напишу её вот так: «Большой кенгуру пропрыгал 24м вперед, а назад на 6метров меньше. Какое расстояние преодолел кенгуру?»
- Какая часть задачи изменилась? Изменился ли вопрос?
- Изменится ли задача, если я напишу её вот так: «Большой кенгуру пропрыгал 24 м вперед, а назад на 6 метров меньше. Какое расстояние преодолел кенгуру, прыгая назад?»
- Какая часть задачи изменилась? Изменился ли вопрос?
- Изменится ли задача, если я напишу её вот так: «Большой кенгуру пропрыгал 24 м вперед и 2 прыжка по 9 метров назад. Какое расстояние преодолел кенгуру?»
- Какая часть задачи изменилась? Изменился ли вопрос?
- Измените условие задачи, на примере того, как я изменила.
= Ученики могут предложить следующую задачу: «Большой кенгуру сделал три прыжка по 8метров, а затем преодолел путь в обратную сторону 18метров. Какое расстояние преодолел кенгуру?»
На этапе формирования умений-копий необходимо ввести понятие «преобразование», объяснив, что это деятельность по изменению вопроса, условия или вопроса и условия. Также необходимо составить алгоритм:
| ||||||||
| ||||||||
| ||||||||
| ||||||||
|
| ||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
З этап: формирование продуктивных умений или умений-знаний.
Цель: формирование умений самостоятельно преобразовывать задачи.
На третьем этапе учитель дает детям задачу, они ее решают, преобразовывают решенную задачу и затем решают преобразованную задачу.
Например, дана задача (Т.Е. Демидова, С.А. Козлова. Моя математика. 2 класс, 2 часть стр. 59 № 6 (а))
- Прочитай задачу: « В двух салонах автобуса находилось по 9 пассажиров в каждом. Сколько пассажиров оказалось в автобусе после остановки, если 4 человека вышли, а 7 вошли?»
- О чем говориться в задаче?
- Что нам известно?
- Какой вопрос ставится в задаче?
- Можем ли мы сразу на него ответить?
- Что нам нужно найти сначала?
- Составьте краткую запись.
- Запишите решение задачи.
2 * 9 = 18 (п) в автобусе было
18 – 4 + 7 = 21 (п) стало
- Измените условие задачи так, чтобы она решалась меньшим количеством действий.
= Ученики могут изменить так: «В автобусе находилось 18 человек. Сколько пассажиров стало в автобусе после остановки, если 4 человека вышли, а 7 вошли?»
- Проверим, правильно ли вы выполнили задание. Решите данную задачу
18 – 4 + 7 = 21 (п) стало
- Как еще можно изменить условие задачи, чтобы она решалась меньшим количеством действий?
= Ученики могут изменить так: «В автобусе находилось 18 человек. Сколько пассажиров стало в автобусе после остановки, если пассажиров стало на 3 человека больше?» и т.д.
- Проверим, правильно ли вы выполнили задание. Решите данную задачу
18 + 3 = 21 (п)
2. Дана задача: «В магазин привезли 4 ящика огурцов по 20 кг в каждом. Сколько всего огурцов привезли?»
- Измени задачу так, чтобы она решалась в два действия.
= Ученики могут предложить следующие задачи: «В магазин привезли 4 ящика огурцов по 20кг в каждом и 2 ящика по 15кг. Сколько всего огурцов привезли?». «В магазин привезли 4 ящика огурцов по 20кг в каждом. Продали 15кг сколько огурцов осталось?» и т.д.
3. Дана задача: «В детский сад привезли 47кг яблок. Это на 15кг больше, чем апельсинов. Сколько килограммов свежих фруктов привезли?»
- О чем говориться в задаче?
- Что нам известно?
- Какой вопрос ставится в задаче?
- Можем ли мы сразу на него ответить?
- Что нам нужно найти сначала?
- Составим краткую запись:
Ябл. _________
Ап. ______
- Запишите решение задачи.
- Преобразуем условие задачи. Давайте воспользуемся краткой записью. Что мы можем в ней изменить? Давайте это сделаем.
Например:
а) Ябл. _________
Ап. ____________
б) Ябл. _________
Ап. ______
Бан. ___
- Сформулируем текст задач на основе сделанных нами кратких записей.
- Решите задачи.
При обучении детей преобразованию задач, большое значение имеет краткая запись, так как детям удобнее увидеть связи между числовыми данными именно на краткой записи, то и изменить их так же удобнее на этой же краткой записи.
Похожие работы
... и обобщение опыта учителей при проведении уроков математики по данной теме. Курсовая работа состоит из введения, двух глав, заключения, списка литературы. Глава I. Методические особенности изучения площади геометрических фигур и единиц ее измерения на уроках математики в начальной школе 1.1 Возрастные особенности развития младших школьников на этапе формирования геометрических представлений ...
... интересует. Соблюдение принципа наглядности – одно из основных требований, которому должно удовлетворять обучение математике в начальных классах. В начальных классах эффективно использовать технические средства обучения (ТСО) и наглядность по несколько минут на различных этапах урока. В процессе работы важно применять технические средства обучения в комплексе с другими средствами наглядности, ...
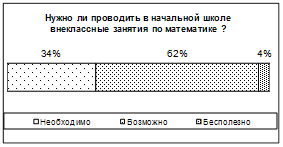
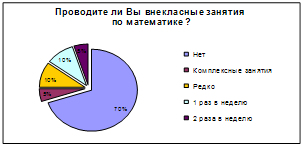
... и младших школьников. Анкета для студентов включала в себя два вопроса, один из которых о том, в чем, по их мнению, заключается развитие математических способностей школьников, а второй ¾ для выяснения отношения студентов к проведению внеклассной работы по математике в начальных классах. Анкета для преподавателей имела своей целью выяснить, проводят ли (а если проводят, то как часто) учителя ...
... натурального ряда. В качестве графической модели используем числовой луч, на котором дети отмечают точки, соответствующие натуральным числам. Смысл действий сложения и вычитания. В курсе математики начальной школы находит отражение теоретико-множественный подход к истолкованию сложения и вычитания целых неотрицательных чисел, в соответствии с которым сложение связано с операцией объединения, ...

0 комментариев