Навигация
Методика ознайомлення із задачами на розкриття конкретного змісту арифметичних дій
2.2 Методика ознайомлення із задачами на розкриття конкретного змісту арифметичних дій
До задач, які розкривають конкретний зміст арифметичних дій, належать задачі на знаходження суми, остачі, добутку, на ділення, на вміщення і рівні частини. Задачі на знаходження суми й остачі —це перші задачі, з якими зустрічаються діти, а тому робота над ними пов'язана з додатковими труднощами: тут учні ознайомлюються, власне, із задачею та її частинами, а також із деякими загальними прийомами роботи над задачею.
Задачі на знаходження суми й остачі вводять одночасно, оскільки одночасно вводять дії додавання і віднімання; крім того, у протиставленні краще формувати вміння розв'язувати ці задачі [6].
У процесі підготовки учнів до ознайомлення із задачею на знаходжен-ня суми ставиться мета: навчити учнів розв'язувати задачі на знаходження суми й остачі, вдаючись до практичних дій з множинами предметів. Учні при цьому не оперують термінами "задача", "умова задачі", "запитання задачі", "розв'язання задачі", "перевірка і відповідь задачі".
При підготовці учнів до ознайомлення із задачею на знаходження остачі діти оперують із множинами предметів або ілюструють ці операції у зошитах. Виконуючи такі практичні завдання, вони усвідомлюють, що операції вилучення підмножини з даної множини відповідає дія віднімання.
Із задачами на знаходження суми й остачі доречно ознайомлювати, спостерігаючи за діями вчителя і дітей. Учні демонструють числові дані і дії, які описуються в задачі. Але результат розв'язання задачі (відповідь) повинен бути прихованим від дітей — інакше учні знаходитимуть відповідь перелічуванням об'єктів, а відтак відпаде необхідність вибору дії та її пояснення. Розв'язання задач на цьому етапі учні записують у вигляді прикладу [5].
На підготовчому етапі ознайомлення із задачею на знаходження суми і остачі задачі дії додавання і віднімання не застосовуються. Відповідь знаходять перелічуванням предметів. Таким чином, текстова задача сприймається учнями як деяка конкретна реальна ситуація, а не як об'єкт вивчення.
Подамо фрагмент уроку з підготовки учнів до ознайомлення із задачами на знаходження суми й остачі.
Задача. У Тараса було 3 зошити в лінійку і 2 зошити в клітинку. Скільки зошитів було у Тараса?
Учитель читає задачу.
— Відповідь знайдемо за допомогою кружечків. Замість зошитів будемо викладати на парті кружечки. Нехай кожен червоний кружечок означає зошит у лінійку, а кожен зелений — зошит у клітинку. У Тараса було 3 зошити в лінійку. Скільки червоних кружечків треба викласти? (3). Що означає кожен червоний кружечок? (Зошит у лінійку). У Тараса було 2 зошити в клітинку. Кружечки якого кольору треба викласти? (Кружечки зеленого кольору). Скільки кружечків зеленого кольору треба викласти? (2). Праворуч від кружечків червоного кольору викладіть стільки кружечків зеленого кольору, скільки зошитів у клітинку було у Тараса. Що означає кожен кружечок зеленого кольору? (Зошит у клітинку). Покажіть усі зошити в лінійку. (Діти обводять тупим кінцем олівця навколо всіх кружечків червоного кольору). Покажіть усі зошити в клітинку. (Учні обводять тупим кінцем олівця навколо всіх кружечків зеленого кольору).

Покажіть усі зошити, які були в Тараса. (Діти обводять тупим кінцем олівця навколо всіх кружечків). Скільки всього зошитів було в Тараса? Полічіть. (5).
На пропедевтичному етапі задачі на знаходження суми будуть розв'язуватися як за допомогою предметних дій, так і за малюнками в зошитах, на дошці або набірному полотні. Оперуючи предметними множинами, діти усвідомлюють, що операції об'єднання відповідає дія додавання.
Покажемо підготовку учнів до ознайомлення із задачею на знаходження остачі.
Задача. Потяг складався з 7 вагонів. Два вагони відчепили. Скільки вагонів залишилось у потязі?
Учитель читає задачу.
— Потяг складався з 7 вагонів. Візьміть синій олівець і зафарбуйте стільки клітинок у зошиті, скільки вагонів було у потязі. Скільки клітинок ви зафарбуєте? (7). Що означає кожна синя клітинка? (Кожна синя клітинка означає один вагон потяга). Скільки вагонів відчепили? (2). Справа перекресліть стільки синіх клітинок, скільки вагонів відчепили.

Скільки клітинок перекреслите? (Дві). Чому перекреслите дві синіх клітинки? (Тому що два вагони відчепили). Що означає кожна перекреслена клітинка? (Кожна перекреслена клітинка означає вагон, який відчепили). Що означає кожна неперекреслена клітинка? (Кожна неперекреслена клітинка означає вагон, який залишився в потязі). Скільки вагонів залишилося у потязі? Полічіть. (5).
Покажемо методику ознайомлення із задачами на знаходження суми й остачі. При цьому важливо, щоб при розв'язанні задач на знаходження суми й остачі учні чітко пояснювали вибір тієї чи іншої дії. Так, наприклад, у задачі "На одній гілці сиділо 3 пташки, а на другій — дві. Скільки пташок сиділо на двох гілках?" вибір дії належить пояснювати так: "Виконаємо дію додавання. Якщо на одній гілці сиділо 3 пташки, а на другій —дві, то число пташок, що сиділи на двох гілках більше, ніж на кожній гілці окремо, тому воно дорівнюватиме сумі чисел 3 і. 2. З плюс 2, буде 5."
До задачі на знаходження остачі: "В Олі було 6 іграшок. Дві іграшки вона віддала Тарасу. Скільки іграшок залишилося в Олі? " вибір дії слід пояснювати так: "Якщо в Олі було б іграшок і дві іграшки вона віддала Тарасу, то в неї залишилось іграшок менше, ніж було. Треба від числа 6 відняти 2.6 мінус 2, дорівнює 4".
Підготовкою до розв'язування задач на знаходження суми й остачі є виконання операцій над множинами: об'єднання двох множин без спільних елементів і вилучення частини множини (цих термінів учням не дають). Діти добре повинні засвоїти, що операція об'єднання множин пов'язана з дією додавання, а операції видалення частини множини — з дією віднімання.
Завдання на оперування множинами слід включати в підготовчий період і в період вивчення нумерації чисел першого десятка. За своєю формою вони не відрізняються від задач, але їх виконують суто практично. Наприклад, учитель читає задачу: «Хлопчик вирізав 3 червоних кружки і 1 голубий. Скільки всього кружків вирізав хлопчик?» Діти кладуть на парти спочатку 3 червоних кружки, потім 1 голубий; присувають їх один до одного і знаходять кількість всіх кружків за допомогою лічби.
Виконавши з дітьми кілька таких вправ, учитель ознайомлює їх з дією додавання: якщо візьмемо 3 і 1 кружок, буде 4 кружки, то кажуть: до 3 додати 1, буде 4; якщо маємо 5 та 2 літаки, буде 7 літаків, то кажуть: до 5 додати 2, буде 7. Виконавши кілька таких вправ, вводять знаки «додати» (плюс), «буде» (дорівнює) і запис на розрізних цифрах: 3+1 =4.
Дуже важливо, щоб ці підготовчі вправи включали в себе різні життєві ситуації.
Наприклад:
а) У дівчинки було 4 кольорових олівці. Брат подарував їй ще 2 олівці. Скільки олівців тепер у дівчинки?
б) В одному акваріумі 3 рибки, а в другому 4 рибки. Скільки рибок у двох акваріумах?
в) 3 гаража спочатку виїхало 6 машин, а потім 3 машини. Скільки всього машин виїхало з гаража?
Розв'язуючи подібні задачі, учні виконують операцію об'єднання неперетинних множин, користуючись наочними посібниками, і пов'язують її з дією додавання. При цьому вони вголос міркують: у дівчинки стало 4 та 2 олівці, буде 6 олівців, отже, треба до 4 додати 2 буде 6. Результат арифметичної дії вони знаходять, рахуючи предмети. Аналогічно проводять підготовчу роботу до розв'язання задач на знаходження суми. При цьому, розв'язуючи задачі на знаходження остачі, спочатку учні виконують лише операцію виділення з множини її підмножини, знаходячи підрахунком предметів відповідь на запитання задачі.
Наприклад, за допомогою наочних посібників (квадратів) учні розв'язують задачу: «У хлопчика було 5 марок. 2 марки він подарував товаришеві. Скільки марок у нього лишилось?». Виконавши операцію виділення, учні міркують: у хлопчика лишилось 5 без двох марок, 3 марки. Виконують ряд таких вправ. Після цього операцію виділення з множини її підмножини пов'язують з дією віднімання. Наприклад, пропонують задачу: «На аеродромі було 9 літаків. 5 літаків полетіло. Скільки літаків лишилось?» Виконавши відповідну операцію на наочних посібниках, учні міркують: на аеродромі лишилось 9 без п'яти літаків, 4 літаки, отже, треба від 9 відняти 5, буде 4. Дуже корисно такими міркуваннями супроводити розв'язання кожної задачі.
Ознайомлюючи дітей з розв'язуванням задач на знаходження суми й остачі, краще перші задачі пропонувати не в готовому вигляді, а складати їх разом, з дітьми.
Першокласникам важко виділяти в задачі числові дані і запитання. Так, повторюючи задачу вони називають разом з даними відповідь або ж відразу називають відповідь, не з'ясувавши відповідної дії. Тому з самого початку треба формувати в дітей загальний прийом роботи над задачею. Щодо цього цілком виправдала себе така методика роботи над простими задачами розглядуваних та всіх інших видів.
Насамперед учитель (а пізніше і діти) читає задачу, учні сприймають її в цілому. При повторному читанні задачі вчителем (або дітьми) учні кладуть на парти цифри, які позначають числові дані задачі, шукане число позначають знаком запитання (пізніше-записують числові дані і шукане в зошити). Це і є процес виділення числових даних і запитання.
Далі учні пояснюють, що показує кожне число, і називають запитання задачі. Тут учні усвідомлюють зв'язок між даними і шуканим.
Потім учням пропонують уявити собі те, про що йдеться в задачі, і розповісти, як вони уявили, що повинно привести дітей до правильного вибору відповідної арифметичної дії.
Тепер можна запропонувати учням назвати дію, за допомогою якої розв'язують задачу, виконати її усно або записати в зошити. Потім формулюють відповідь на запитання задачі і записують тоді, коли діти вмітимуть писати. Відповідь можна записати коротко, дати усно розгорнуте формулювання або просто підкреслити в записі розв'язання.
Якщо під час розв'язання задач учні багато разів виконуватимуть такі завдання в певному порядку, то в них поступово сформується вміння працювати над задачею відповідно до цих завдань. Це дасть дітям можливість надалі самостійно розв'язувати задачі.
Під час розв'язання перших готових задач дуже важливо продовжити роботу над засвоєнням дітьми термінології, яка стосується задачі і її розв'язання. Для цього корисно включати такі вправи: після розв'язування задачі викликати до столу чотирьох учнів: перший з них говорить слова «умова задачі» і формулює умову; другий — «запитання задачі» і називає запитання; третій — «розв'язання задачі», після чого називає розв'язання; четвертий говорить слово «відповідь» і формулює її. Внаслідок виконання на різних уроках кількох таких вправ діти міцно засвоюють згадані терміни.
Розв'язання задач на перших уроках слід записувати у вигляді виразу за допомогою розрізних цифр і відповідних знаків, а як тільки діти навчаться виконувати арифметичні записи в зошиті, можна записувати розв'язання.
Працюючи над узагальненням способу розв'язування, треба включати вправи на самостійне розв'язування задач, при цьому діти в думці пояснюють, чому вони обрали дію додавання або віднімання. На цьому ступені треба попутно встановити нові зв'язки: якщо об'єднують непорожні множини без загальних елементів, то в об'єднанні виходить елементів більше, ніж у кожній з множин (у коробці було 6 м'ячів, коли поклали ще 2 м'ячі, їх стало більше). Якщо з множини беруть непорожню множину, в якій елементів менше, ніж у даній множині (у коробці було 8 м'ячів, коли взяли 2 м'ячі, то лишилось менше); щоб дістати більше, треба додавати, а менше — віднімати. Засвоєння цих зв'язків буде підготовкою до ознайомлення з розв'язуванням задач на збільшення і зменшення числа на кілька одиниць. Як тільки будуть введені задачі нових видів, корисно розглядувані задачі розв'язувати разом з ними: наприклад, запропонувати задачу на знаходження суми, відразу ж задачу на знаходження невідомого доданка і порівняти їхні розв'язання.
Дуже корисно включати розв'язування задач підвищеної трудності, а також вправи на складання і перетворення задач. Досвід показав, що ці останні вправи доцільно вводити в такій послідовності: складання задачі за картинкою, предметами в класі, предметами, яких немає, за умовою, коротким записом, запитанням, розв'язанням, зазначеною дією; пізніше перетворюють задачу на знаходження суми в задачу на знаходження невідомого доданка і навпаки, задачу на знаходження остачі в задачу на знаходження невідомого зменшуваного або від'ємника або навпаки. Такий порядок введення вправ забезпечує правильний перехід від конкретних дій над предметами до дій над ними за уявленням.
Задачі на знаходження суми однакових доданків (добутку) вводять у II класі, розкриваючи конкретний зміст дії множення. Підготовчу роботу до введення цих задач розпочинають у І класі, вивчаючи додавання і віднімання. Вона зводиться до розв'язування задач на знаходження суми однакових доданків за допомогою оперування предметами, про які йдеться в задачі, і виконання дії додавання.
Спочатку пропонують вправи виду: «Покладіть по 2 кружки З рази. Скільки всього кружків ви поклали?» Діти розкладають на партах по 2 кружки 3 рази і знаходять число всіх кружків дією додавання: 2+2+2 = 6. Далі встановлюють, що доданки цієї суми однакові і що їх три.
Аналогічно розглядають сюжетні задачі, наприклад: «Мама поклала пиріжки на 4 тарілки, по 3 пиріжки на кожну. Скільки всього пиріжків на цих тарілках?»
Корисно для підготовки учнів включати вправи на складання задач за їх розв'язанням. Так, за розв'язанням 5+5+5=15 діти можуть скласти різні задачі, наприклад: «У хлопчика було 3 монети по 5 коп. Скільки грошей було в хлопчика?».
У другому класі при ознайомленні з розв'язуванням задач на знаходження добутку учні мають усвідомити, що суму однакових доданків можна замінити добутком. Вони повинні засвоїти новий запис і розуміти, що означає кожне число в цьому записі.
Підготовка учнів до ознайомлення із простими задачами на знаходження добутку як суми однакових доданків зводиться до розв'язування задач на знаходження суми однакових доданків. Останні розв'язуються учнями на основі практичних дій з предметами або їх замінниками, про які говориться в задачі, або на основі розгляду малюнків. Основна мета розв'язування таких задачі методики роботи над ними — підготувати учнів до розкриття змісту дії множення, ознайомити учнів із словами і словосполученнями, що відповідають дії множення: однакові доданки, рази, сума однакових доданків.
У II класі вводять ділення. Конкретний зміст цієї арифметичної дії розкривають під час розв'язування задач на ділення на рівні частини, а далі на ділення на вміщення. Спочатку вводять ділення на вміщення, а потім на рівні частини. Це зумовлено тим, що практично виконувати операції над множинами при розв'язуванні задач із застосуванням ділення на вміщення легше, ніж при розв'язуванні задач із застосуванням ділення на рівні частини. Крім того, операції, які виконують при розв'язуванні задач із застосуванням ділення на рівні частини, як побачимо далі, включають у себе операції, які виконують при розв'язуванні задач із застосуванням ділення на вміщення.
Покажемо особливості підготовки учнів до ознайомлення із простими задачами на ділення (ділення на вміщення і на рівні частини).
Вправа 1. Фронтальна практична робота на ділення на рівні частини.
¾ До дошки вийдуть Семен, Оля і Леся. Цим учням треба роздати 12 зошитів порівну. Зошити буде роздавати Оленка. Скільки зошитів треба взяти Оленці, щоб дати кожному учневі по одному зошиту?
¾ Щоб кожному учневі дати по одному зошиту, треба Оленці взяти три зошити.
¾ Чому треба взяти три зошити?
¾ Тому, що зошити роздають трьом учням. (Оленка бере 3 зошити і роздає кожному учневі по одному).
¾ Візьми, Оленко, ще 3 зошити і дай кожному учневі по другому зошиту. (Оленка роздає по другому зошиту.) Візьми, Оленко, ще 3 зошити, дай кожному по третьому зошиту. (Оленка роздає по третьому зошиту кожному учневі, а потім і по четвертому.)
¾ Чи всі зошити роздала Оленка?
¾ Всі зошити роздала Оленка учням.
¾ По скільки зошитів одержав кожний учень?
¾ Кожний учень одержав по 4 зошити.
o Вправа 2. Робота з індивідуальним роздатковим матеріалом.
¾ Покладіть на парту 8 кружечків. (Учні виконують.) Розкладіть пі кружечки на дві купки порівну. Як будете розкладати ні кружечки?
¾ Візьміть 2 кружечки і покладіть їх по одному на купки. (Учні виконують.)
¾ Візьміть другий раз кружечки і розкладіть їх на купки. Скільки кружечків треба взяти?
¾ Треба взяти 2 кружечки.
¾ Чому треба взяти 2 кружечки?
¾ Тому що їх треба розкласти на 2 купки по одному.
¾ Візьміть 2 кружечки і покладіть їх по одному на купки. Закінчіть розкладати кружечки на купки. (Учні виконують.) Чи всі кружечки розклали?
¾ Всі кружечки ми розклали.
¾ По скільки кружечків у купці?
¾ По 4 кружечки в кожній купці.
Вправа 3. У таблиці (або на набірному полотні) викладено предметні картинки запряжок, по 3 собаки в кожній.
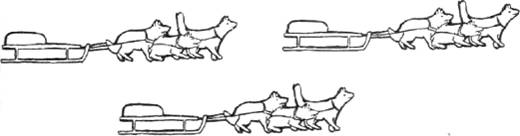
· Скільки санок ви бачите на набірному полотні?
· Скільки собак у кожній запряжці?
· Скільки всього собак у всіх запряжках?
· Як взнали? Поясніть.
Ознайомлення учнів з розв'язуванням задач на ділення на вміщення передбачено в II класі. Наприклад, пропонують задачу: «12 морквин зв'язали в пучки, по 4 морквини в кожному. Скільки вийшло пучків?» На набірному полотні один з учнів розкладає 12 морквин по 4, а решта учнів виконує те саме за допомогою будь-яких предметів на партах. Виконавши це, підраховують, скільки вийшло пучків. Розв'язання записують так: 12:4=3.
Відповідь: 3 пучки.
Спочатку під час розв'язування задач треба користуватися наочними посібниками, результат знаходити за допомогою лічби, після чого записувати розв'язання. Поступово учні вибиратимуть дії за уявленням, не вдаючись до наочних, посібників, а результати визначатимуть, користуючись таблицею. Однак у разі утруднень треба пропонувати дітям виконувати оперування множинами.
Підготовкою до розв'язування задач на ділення на рівні частини буде практичне виконання, починаючи з І класу, операцій над множинами:
а) Розкладіть 6 кружків у 2 ряди порівну. Скільки кружків у кожному ряді?
б) Юра знайшов 12 жолудів і розклав їх у 4 коробки порівну. Скільки жолудів він поклав у кожну коробку?
Спочатку роботою керує вчитель.
— Скільки треба взяти кружків, щоб покласти в кожний ряд по одному кружку? Так, стільки, скільки рядів. Візьміть 2 кружки і покладіть у кожний ряд по одному. Візьміть ще стільки, щоб покласти в кожний ряд по одному, і розкладіть їх. Чи всі кружки розклали? Візьміть ще стільки кружків, щоб у кожний ряд покласти по одному, і розкладіть їх. Чи всі кружки розклали? По скільки кружків у кожному ряді? Ви 6 кружків поділили на 2 рівні частини і дістали по 3 кружки в кожній частині.
При такому оперуванні множинами явно виступає зв'язок між: задачами із застосуванням ділення на рівні частини і на вміщення: у кожній частині буде по стільки кружків, скільки разів по 2 кружки міститься в 6 кружках.
У І класі подібні вправи учні виконують практично, не записуючи розв'язання, а результат знаходять за допомогою лічби.
У II класі вводять розв'язання задач на ділення на рівні частини. Спочатку задачі розв'язують, практично оперуючи множинами, після чого записують розв'язання. Наприклад, пропонують задачу: «Мама роздала 6 груш 3 дітям порівну. Скільки груш одержала кожна дитина?» Оперуючи наочними посібниками, учень міркує: «Беру стільки груш, щоб кожній дитині дати по одній, тобто 3 груші, і даю по одній, беру ще 3 груші і даю по одній; кожна дитина одержала по 2 груші».
Розв'язання записують так: 6:3=2.
Відповідь: По 2 груші.
Задачі на ділення можна розв'язувати і не використовуючи наочності тоді, коли діти навчаться знаходити дію за уявленням, а результат ділення на підставі таблиці множення.
Похожие работы
... дповідь. · На кожній тарілці 3 помідори. · Запишіть: "Відповідь. З помідори". Запис у зошиті. 6:2=3 (п.). Відповідь. 3 помідори. Охарактеризовані методичні прийоми опрацювання простих задач на розкриття конкретного змісту арифметичних дій постали в основі формуючого експериментального дослідження, покликаного удосконалити уміння і навички учнів розв’язувати такий тип задач. Таким чином, ...
... правильність результатів; показувати, до яких негативних результатів можуть привести допущені в розв'язанні задачі помилки. Розглянемо прийоми перевірки правильності розв'язування задач та питання методики формування у молодших школярі" уміння застосовувати їх. У 1-4 класах доцільно поступово запроваджувати такі прийоми перевірки; порівняння результату, який дістати учні в процесі розв'язання ...
... школярів математичних уявлень і понять. Усвідомлення їх є важливим як для практично-життєвої підготовки учнів, так і для подальшого засвоєння математичних знань у середніх класах. 1.2 Проблема формування вмінь у другокласників розв’язувати складені задачі Традиційно ознайомлення з поняттям “складена задача” здійснюється в 2-му класі на задачах на знаходження остачі, й ці задачі пропонуються ...
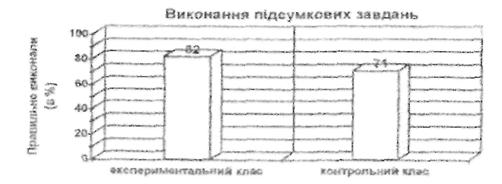
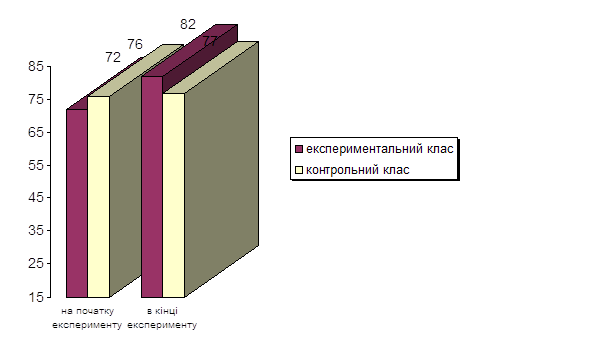
... ійований підхід, значно вищий, ніж у контрольному, причому особливо відрізняються результати розв’язання додаткового завдання. Ми пояснюємо це цілеспрямованою роботою диференційованого підходу у процесі навчання молодших школярів розв’язувати текстові задачі, яка проводилася відповідно до завдань формуючого експерименту, що привело до позитивних зрушень у розвитку мислення школярів. 2.3 Аналіз ...






0 комментариев