Результати експериментального дослідження

2.3. Результати експериментального дослідження

Дипломне дослідження мало теоретико-експериментальний характер і проводилося у два етапи. На теоретичному етапі (2006–2007 навчальний рік) була визначена сфера і проблема дослідження; вивчалася педагогічна, методична література з даної теми; аналізувалася робота вчителів початкових класів у галузі методики розв’язування простих задач, що розкривають конкретний зміст арифметичних дій, шляхом диференційованого навчання; формулювалася гіпотеза та завдання дослідження.

В процесі експериментального етапу (2007–2008 навчальний рік) – на основі напрацьованої теоретичної інформації здійснювався формуючий експеримент, пов’язаний із формуванням у молодших школярів умінь і навичок розв’язування простих задач, що розкривають конкретний зміст арифметичних дій, з використанням диференційованого підходу, вивчалася його ефективність та практична значущість.

Експериментальне дослідження ми проводили у Бзовицькій початковій школі Зборівського району Тернопільської області. Ним було охоплено 23 учні 1-А класу (експериментального) і 21 учень 1-Б класу (контрольного). У процесі формуючого експерименту ми пропонували першокласникам систему простих задач, що розкривають конкретний зміст арифметичних дій, різних видів. Ці задачі використовувалися як на уроках, так і на позакласних заняттях з математики і пропонувалися для самостійної роботи учнів.

Залучаючи здібних учнів до розв'язування простих задач, що розкривають конкретний зміст арифметичних дій, ми тим самим інтенсифікували процес навчання, розвивали творче мислення школярів, формували стійкий інтерес до предмета. Така робота виявилася ефективною тільки за умови доброзичливого явлення до кожного школяра, заохочення його до висловлювання творчих ідей і постановки найрізноманітніших запитань.

Виявлення ефективності розробленої системи задач у формуванні математичних уявлень і понять у молодших школярів ми здійснювали на основі порівняння сформованості відповідних навичок та вмінь в учнів експериментального класу порівняно з контрольним, де використовувалася звичайна система навчання.

На основі відповідних показників ми визначили уміння і навички, пов’язані із розв’язуванням різновидів простих задач, що розкривають конкретний зміст арифметичних дій. За рівнем розвитку даних умінь ми визначили три рівні сформованості математичних уявлень і понять учнів про прості задачі, що розкривають конкретний зміст арифметичних дій:

1)  високий – у школяра сформовані уміння, пов’язані із розв’язуванням простих задач, що розкривають конкретний зміст арифметичних дій, і здатність безпомилкового розв’язання задачі або самостійного виправлення допущених помилок при зауваженні вчителя;

2) середній – учень виконує усі попередні завдання на належному рівні, але припускається кількох неістотних помилок, які виправляє з незначною допомогою вчителя;

3) низький – в учня не сформовані пропедевтичні уміння розв’язування простих задач, що розкривають конкретний зміст арифметичних дій, не розвинені загальні уміння розв’язування задач з математики і відповідно не сформовані практичні уміння розв’язування задач даного виду.

Робота, яка проводилася нами в експериментальному класі, позитивно вплинула на підвищення якості знань і вмінь молодших школярів. Так, учні експериментального класу значно краще виконали запропоновані завдання, ніж учні контрольного.

Отримані результати формуючого експерименту підтвердили гіпотезу, що використання запропонованої системи розв’язування простих задач, що розкривають конкретний зміст арифметичних дій, з використанням диференційованого підходу позитивно вплинули на формування відповідних уявлень і понять в учнів експериментального класу.

Таким чином, ми отримали результати, які підтвердили ефективність формуючого експерименту. Із 23 учнів експериментального класу 5 школярів продемонстрували високий рівень сформованості навичок розв’язування простих задач, що розкривають конкретний зміст арифметичних дій, 15 – середній і 3 – низький.

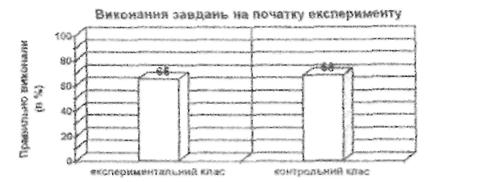
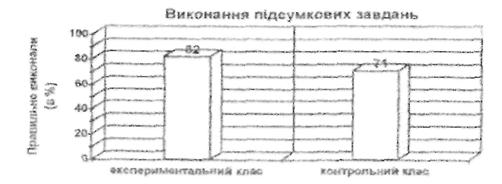
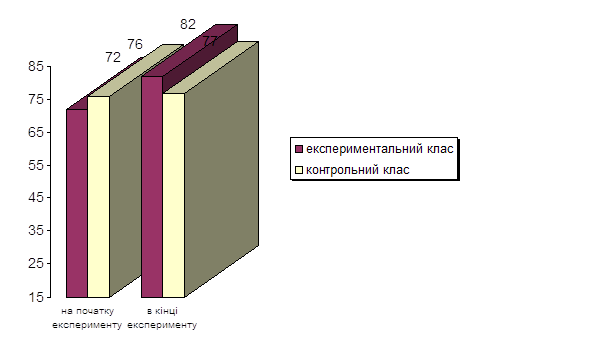
У контрольному класі (21 учень) високий рівень розвитку навичок розв’язування простих задач, що розкривають конкретний зміст арифметичних дій, мають 2 учні, середній – 11 і низький – 8 школярів. Порівняно з початком експерименту, показники сформованості відповідних умінь розв’язувати прості задачі, що розкривають конкретний зміст арифметичних дій, зросли в обох класах (початковий рівень відповідно 76 і 72%). Проте в експериментальному класі наприкінці дослідження ці показники виявилися значно вищими (відповідно 77 і 82% – див. діаграму).

 

Діаграма

Загальний рівень сформованості умінь розв’язування простих задач, що розкривають конкретний зміст арифметичних дій, в експериментальному і контрольному класах на початку і в кінці експерименту

Проведення експериментального дослідження дало змогу виявити і оцінити ефективність використання пропонованої системи простих задач, що розкривають конкретний зміст арифметичних дій, і простежити процес розвитку умінь розв’язувати дані задачі порівняно з навчанням дітей в контрольному класі. У процесі використання розробленої системи простих задач, що розкривають конкретний зміст арифметичних дій, в учнів експериментального класу порівняно з контрольним значно підвищився рівень сформованості відповідних умінь, що свідчить про ефективність застосовуваного напрямку роботи.

Висновки

На сучасному етапі розбудови початкової освіти розв’язування простих текстових задач у навчанні математики переслідує такі цілі: формування в учнів загального підходу, загальних умінь і здібностей розв’язання будь-яких задач; пізнання і більш глибоке оволодіння математичними поняттями, що вивчаються, і деякими загальнонауковими й загальножиттєвими поняттями; оволодіння поняттями моделі й моделювання і власне математичним моделюванням; розвиток мислення, кмітливості учнів, творчого потенціалу.

Через розв'язування задач діти ознайомлюються з важливими фактами, які мають пізнавальне і виховне значення. Текстові задачі допомагають розкрити опосередковані зв’язки математики з навколишнім середовищем і практичною діяльністю людей, реалізувати пізнавальні, розвивальні і виховні функції навчання. Проте ряд аспектів формування вмінь розв’язувати прості задачі, що розкривають конкретний зміст арифметичних дій, залишилися нерозкриті, зокрема обсяг теоретичних знань про прості задачі, що розкривають конкретний зміст арифметичних дій, і процес її розв’язування у початкових класах; добір різнорівневих завдань, спрямованих на формування вмінь розв’язувати ці задачі; способи раціонального поєднання фронтальної, групової та індивідуальної форм роботи на уроках математики при розв’язуванні простих задач в умовах диференційованого навчання у початковій ланці школи.

Прості задачі в системі навчання математики відіграють дуже важливу роль. За допомогою розв'язування простих задач формують одне з центральних понять початкового курсу математики — поняття про арифметичні дії і ряд інших понять. Уміння розв'язувати прості задачі є підготовчим ступенем опанування учнями умінь розв'язувати складені задачі, бо розв'язування складеної задачі зводиться до розв'язування ряду простих задач. Розв'язуючи прості задачі, діти вперше ознайомлюються з задачею і її складовими частинами. У зв'язку з розв'язуванням простих задач діти опановують основні прийоми роботи над задачею. Тому вчитель повинен знати, як організувати роботу над простими задачами кожного виду.

Щоб розв'язати просту задачу, учень повинен виділити в ній відоме й невідоме, а потім вибрати арифметичну дію чи скласти рівняння, за допомогою яких знайти невідоме. Для цього треба перевести на математичну мову відношення між даними і шуканими величинами, про які йдеться в задачі. Наше дослідження присвячене роботі над задачами першої групи – це задачі на знаходження суми, остачі, добутку, на ділення.

Інтенсивність розвитку вмінь молодших школярів у розв'язуванні простих задач, що розкривають конкретний зміст арифметичних дій, визначається, передусім, змістом задач і методами керування цим процесом. Формування навичок розв'язування простих арифметичних задач і розвиток умінь розв'язувати складені задачі на початковому етапі відбувається за допомогою наслідування зразків і постійної практики. Проте кожна задача, розв'язана з певною часткою власних зусиль, стає зразком для розв'язання інших задач. Тому методи навчання математики і вироблення умінь в учнів повинні бути спрямовані на перенесення здобутих результатів на нові об'єкти, нові задачі, в нові умови, на порівняння схожих чи взаємопов'язаних між собою задач.

Важливе значення для розв'язування простих задач, що розкривають конкретний зміст арифметичних дій, має ретельний добір навчальних завдань, які мають відповідати певним загально-методичним вимогам: забезпечувати засвоєння учнями програмового матеріалу з математики і, зокрема, формувати в них знання про задачу, її склад і процес розв'язування, вчити використовувати набуті знання в різних ситуаціях; зміст завдань має відповідати темі уроку і меті вивчення матеріалу, а числові дані — програмовим вимогам; послідовність застосування вправ має сприяти свідомому засвоєнню теоретичних знань і вмінню розв'язувати задачі, розвитку прийомів розумової і творчої діяльності школярів; створювати умови для узагальнення способів діяльності; відповідати логіці й структурі процесу формування вмінь; кількість вправ повинна відповідати індивідуально-психологічним особливостям школярів і бути достатньою для формування певного вміння або навички.

Дипломне дослідження мало теоретико-експериментальний характер і проводилося у два етапи. На експериментальному етапі на основі напрацьованої теоретичної інформації здійснювався формуючий експеримент, пов’язаний із формуванням у молодших школярів умінь і навичок розв’язування простих задач, що розкривають конкретний зміст арифметичних дій, з використанням диференційованого підходу, вивчалася його ефективність та практична значущість. Залучаючи здібних учнів до розв'язування простих задач, що розкривають конкретний зміст арифметичних дій, ми тим самим інтенсифікували процес навчання, розвивали творче мислення школярів, формували стійкий інтерес до предмета.

Робота, яка проводилася нами в експериментальному класі, позитивно вплинула на підвищення якості знань і вмінь молодших школярів. У процесі використання розробленої системи простих задач, що розкривають конкретний зміст арифметичних дій, в учнів експериментального класу порівняно з контрольним значно підвищився рівень сформованості відповідних умінь, що свідчить про ефективність добірки простих задач, що розкривають конкретний зміст арифметичних дій, у формуванні математичних уявлень і понять у молодших школярів.

Список використаної літератури

 

1.  Анкудинова Т.Г. Работа над текстовой задачей // Начальная школа, 1997, № 7.-с. 42-43.

2.  Бантова М.О. Методика викладання математики в початкових класах. – К.: Вища школа, 1982. – 288 с.

3.  Басангова Р.Е. Стимулювання пізнавальної діяльності учнів в ході розв’язування задач // Поч. школа. – 1989. – №1. – С. 40-44.

4.  Белова Е.С. Развитие диалога в процессе решения школьниками мыслительных задач // Вопр. психологии. – 1991. – №2. – С. 148-153.

5.  Богданович М.Б. Методика розв’язування задач у початковій школі. – К.: Вища школа, 1990. – 234 с.

6.  Богданович М.Б., Козак М.В., Король Я.А. Методика викладання математики в поч. кл. – Тернопіль: Навч. книга – Богдан, 2001. – 368 с.

7.  Богданович М.В. Урок математики в початковій школі: Пос. для вчителя. – К.: Рад. школа, 1990. – 192 с.

8.  Богоявленский Д.Н., Менчинская Н.А. Психология усвоения знаний в школе. – М.: Просвещение, 1959. – 242 с.

9.  Бородулько М.А., Стойлова Л.П. Обучение решению задач и моделирование // Начальная школа, 1996, № 8. - с. 26-31.

10.  Братанки О. Реалізація диференційованого навчання в умовах комбінованого уроку // Рідна школа. – 2000. – №11. – С. 49–52.

11.  Василенко І.З. Методика викладання математики в початкових класах. – К.: Просвіта, 1971. – 376 с.

12.  Вікова та педагогічна психологія (О.В.Скрипченко, Л.В.Долинська, З.В.Огороднійчук та ін.-К.: Просвіта, 2001.-416с.

13.  Володько В.М. Індивідуалізація і диференціація навчання; понятійно-категоріальний аналіз // Пед. і психол. – 1997. – №4. – С. 9–17.

14.  Волокитина М.Н. Очерки психологии школьников первого класса /Под ред. М.Смирнова. – М.: Учпедгиз, 1951. – 102с.

15.  Газдун М.І. Як учити молодших школярів розв’язувати задачі // Поч. школа. – 1988. – №11. – С. 70-72.

16.  Галузинский В.М. Индивидуальный подход в воспитании учащегося. – К.: Высшая школа, 1982. – 240 с.

17.  Гільбух Ю.З. Діагностика мислительних здібностей // Рад. школа. – 1990. – №12. – С. 19-26.

18.  Глушков И.К. Дифференцированная работа над задачами // Нач. школа. – 1985. – №2. – С. 34-35.

19.  Глушков И.К. Составление задач по выражению // Начальная школа, 1995, №12.-с.50-55.

20.  Гора Т., Логачевська С. Диференційований підхід до розв'язування текстових задач // Поч. школа. – 2002. - №1. – С. 17-22.

21.  Гословська І.Г., Скворцова С.О. Формування позитивної мотивації навчання в молодших школярів на уроках математики //Наука і освіта, - 2000. - №6. – с.18-24.

22.  Давыдов В.В. Проблемы развивающего обучения. – М.: Просвещение, 1986. – 220 с.

23.  Друзь Б.Г. Виховання пізнавальних інтересів молодших школярів у процесі навчання. – К.: Рад. школа, 1978. – 126 с.

24.  Друзь Б.Г. Творчі вправи з математики для початкових класів. – К.: Рад. школа, 1988. – 144 с.

25.  Завізєна Н. Тлумачення індивідуалізованого навчання у психолого-педагогічній літературі // Рідна школа. – 1999. – №9. – С. 55–57.

26.  Заїка А., Богданович М. Учням про задачу і процес її розв’язування // Початкова школа. – 2000. – № 11. – С. 28-29.

27.  Захарова А.М. Розвивальне навчання математики в початковій школі // Психол. і педагогіка. – 2000. – №1. – С. 21-27.

28.  Истомина Н.Б., Шикова В.Н. Формирование умений решать задачи различными способами // Нач. школа. – 1985. – №9. – С. 50-54.

29.  Калмыкова З.И. Пути развития продуктивного мышления школьников // Вопр. психологии. – 1978. – №3. – С. 143-148.

30.  Король Я.А. Математика в початкових класах: Культура усного і писемного мовлення. – Тернопіль: Навч. книга – Богдан, 2000. – 160 с.

31.  Король Я.А. Розв’язування текстових задач різними способами // Актуальні проблеми розбудови національної освіти. Ч. ІІІ. – К.-Херсон, 1997. – С. 76-78.

32.  Корчевська О.П. Робота над завданнями підвищеної складності з математики в початкових класах. – Тернопіль: Підручники і посібники, 2001. – 112 с.

33.  Костюк Г.С. Навчально-виховний процес і психічний розвиток особистості. – К.: Рад. Школа, 1989. – 386с.

34.  Кочина Л., Листопад Н. Математика: навчальні програми для чотирирічної початкової школи // Поч. школа. – 2001. – №7. – С. 17-20.

35.  Кубрак В.І. Організація і керівництво диференційованим навчанням // Поч. шк. – 1991. – №4. – С. 52–55.

36.  Люблінська Г.О. Дитяча психологія. – К.: Вища школа, 1974. – 356 с.

37.  Максимов Л.К. Психологические особенности математического мышления школьников // Новые исследования в психологии. – №1. – М.: Педагогика, 1979. – С. 51-54.

38.  Маркова А.А. Формирование мотивации обучения в школьном возрасте. – М.: Педагогика, 1983. – 124 с.

39.  Матюшкин А.М. Проблемные ситуации в мышлении и обучении. – М.: Просвещение, 1972. – 204 с.

40.  Махмутов М.И. Об индивидуализации обучения // Нар. образование. – 1964. – №2. – С. 12–18.

41.  Моро М.Г., Пишкало А.М. Методика навчання математики в 1-3 класах. – К.: Рад. школа, 1979. – 376 с.

42.  Мурачковский Н.И. Психологические аспекты организации дифференцированных форм работы на уроке // Сов. педагогика. – 1989. – №10. – С. 35–40.

43.  Осинская В.Н. Формирование умственной культуры учащихся в процессе обучения математике. – К.: Рад. школа. – 1989. – 192 с.

44.  Павліченко О.І. Питання методики дидактичних досліджень. – К.: Вища школа, 1992. – 157 с.

45.  Пентегова Г.А. Развитие логического мышления на уроках математики // Нач. школа. – 2000. – №11. – С. 74.

46.  Поляк Г.Б. Як навчати розв’язуванню задач у початковій школі. – К.: Освіта, 1952. – 194 с.

47.  Рамендик Д.М. Стиль мышления и способ взаимодействия партнеров при совместном решении задач // Психологический журнал. – 1996. – №5. – С. 20.

48.  Савченко О.Я. Дидактика початкової школи. – К.: Абрис, 1997. – 416 с.

49.  Савченко О.Я. Реформування змісту початкової освіти // Поч. школа. – 1996. – №1. – С. 4-8.

50.  Савченко О.Я. Сучасний урок в початкових класах. – К.: Магістр-S, 1996. – 384 с.

51.  Сорокин П.И. Занимательные задачи про математике. С решениями и методическими указаниями. Пос. для детей 1-4 кл. – М.: Просвещение, 1977. – 170 с.

52.  Туркина В.М. Задачи в 1 классе // Начальная школа. – 1996. - № 9. - с.51-53.

53.  Тягур Р.С. Ефективність системи диференційованого навчання // Поч. шк. – 1992. – №11-12. – С. 25–39.

54.  Халуповский М.Д. Одна из форм краткой записи при решении задач // Начальная школа, 1993, № 12.- С.32-34.

55.  Харишин О. Активізація розумової діяльності учнів //Початкова освіта – 2001. - №5. – с.4.

56.  Царева С.Е. Виды работ с задачами на уроке математики // Нач. школа. – 1990. – №10. – С. 37-42.

57.  Шадрина И.В. Использование графических схем при работе над текстовой задачей // Начальная школа. – 1995. - № 3. - С.39-61.

58.  Шевченко А. Розв’язування задач різними способами // Поч. школа. – 2000. – №7. – С. 22-25.

59.  Шипова Р.Н., Шипова Л.Р. О более полной реализации функций текстовых задач в практической деятельности // Начальная школа, 1995.- № 3. - С.77-80.

60.  Шмырёва Г.Г. Дифференцированные задания при работе над ошибками в решении задач // Нач. школа. – 1986. – №2. – С. 34-35.

Додаток А. Система задач на знаходження суми для 1 класу

 

1.  На алеї біля школи посадили 4 ялини і 3 берези. Скільки дерев посадили?

2.  По дорозі їдуть машини. Серед них 4 легкових і п'ять вантажних. Скільки машин їдуть по дорозі?

3.  У хатинці живуть коза і семеро козенят. Скільки тварин живе у хатинці?

4. Борис знайшов п'ять великих грибів і 3 маленьких. Скільки грибів знайшов Борис?

5.  На кущі бузку було 7 квітучих гілок. За день розквітли ще дві гілки. Скільки квітучих гілок стало на кущі бузку?

6.  В Олі було два плаття: жовте і голубе. До свята мама пошила їй ще біле і зелене плаття. Скільки платтів стало в Олі?

7.  Вовк прийшов у кімнату сміху. Там вже були три зайці і дві білки. Скільки звірят було в кімнаті сміху до того, як прийшов вовк?

8.  З городу принесли 5 морквин і 4 буряки. Скільки овочів принесли з городу?

9.  З городу принесли 6 помідорів і 3 огірки. Скільки овочів принесли з городу?

10.У хованки гралися дві дівчинки і троє хлопчиків. Скільки дітей гралося у хованки?

11. Зайченята допомагали мамі мити посуд. Менше зайченя помило три чашки, а більше — п'ять. Скільки чашок вимили зайченята?

12.Мама купила три пиріжки з м'ясом і стільки ж пиріжків з сиром. Скільки пиріжків купила мама?

13.Мама купила три пиріжки з м'ясом і 4 пиріжки з рисом. Дві пиріжки з м'ясом з'їли діти. Скільки всього пиріжків купила мама?

14.У шафі лежало три великих і чотири маленьких наволочки. Скільки наволочок лежало у шафі?

15.Біля берега стояло п'ять синіх човнів і шість зелених. Скільки човнів було біля берега?

16.У вазі були груші. Петрусь взяв три груші, а Миколка — чотири. Фруктів у вазі не стало. Скільки груш було у вазі?

17.На стоянці було дев'ять машин. Серед них — три вантажні і дві легкові. Скільки всього вантажних і легкових машин було на стоянці?

18.У банку налили дві склянки гарячої води і три склянки холодної. Скільки склянок води налили у банку?

19.Після сніданку на столі залишилося три бутерброди з сиром і два бутерброди з ковбасою. Скільки всього бутербродів залишилося на столі?

20.На гойдалках гойдалося четверо зайченят, двоє ведмежат і білка. Скільки зайченят і ведмежат гойдалося на гойдалках?

21.У дитячий садок привезли три бідони з молоком і стільки ж бідонів з кефіром. Скільки всього бідонів привезли у дитячий садок?

22.Червона Шапочка несла в кошику 6 пиріжків з капустою і 3 пиріжки з м'ясом. Скільки всього пиріжків у кошику Червоної Шапочки?

23.Марійка відрізала чотири сантиметри стрічки, а потім — ще п'ять. Скільки сантиметрів стрічки відрізала Марійка?

24.У вазу поставили чотири червоні троянди, дві білі і одну жовту. Скільки червоних і білих троянд поставили у вазу?

25.У вазу поставили три білі троянди. Скільки всього червоних І білих троянд поставили у вазу?

26.У саду посадили три кущі смородини. Скільки всього кущів смородини і аґрусу посадили в саду?

27.Після тренування у спортивній залі залишилося чотири дівчинки і три хлопчики. Скільки дітей залишилось у залі?

28.Зі стоянки виїхало спочатку чотири таксі, а потім ще п'ять, Скільки таксі виїхало зі стоянки?

29.Руслан повісив на ялинку 7 іграшок. Сестра допомогла йому повісити ще три прикраси. Скільки іграшок повісили діти на ялинку?

30.У пакеті було 4 яблука і 6 груш, а у вазі — три яблука. Із пакета яблука переклали у вазу. Скільки яблук стало у вазі?

31.У Петра було п'ять горіхів. Ще три горіхи йому дала сестра. Скільки горіхів стало у Петра?

32.Андрій і Тарас читали казку. Андрієві залишилося прочитати ще дві сторінки, а Тарасу — три. Скільки сторінок залишилося прочитати обом хлопчикам?

33.Біля годівниці було 8 синичок і два горобчики. Скільки всього пташок було біля годівниці?

34.У глечик можна влити 5 склянок молока, а в пляшку — 2 склянки. Скільки склянок молока потрібно взяти, щоб наповнити глечик і пляшку?

35.В автобусі було 3 вільних місця. Після зупинки звільнилося ще 5 місць. Скільки вільних місць стало у автобусі?

36.На тарілці було 6 пиріжків з капустою і три пиріжки з повидлом. Скільки пиріжків було на тарілці?

37.Надійка зірвала 3 червоних квітки і 7 жовтих. Скільки всього квіток зірвала Надійка?

Додаток Б. Система задач на знаходження остачі для учнів 1 класу

 

1.  У зоопарку жило 5 жираф. Двох жираф передали в інший зоопарк. Скільки жираф залишилось у зоопарку?

2.  У зоопарку було 9 лисиць. Трьох лисиць передали в інший зоопарк. Скільки лисиць залишилось у зоопарку?

3.  У ліфті їхало четверо чоловіків. На третьому поверсі ліфт зупинився і з нього вийшло троє чоловіків. Скільки людей залишилось у ліфті?

4.  Зайченя має намалювати 4 картини, щоб подарувати їх осликові. Воно намалювало 1 картину. Скільки картин залишилося ще намалювати?

5.  З городу принесли 8 помідорів і 5 огірків. З чотирьох огірків зробили салат. Скільки огірків залишилось?

6.  У кошику було 8 цибулин. Дві цибулини взяли для салату. Скільки цибулин залишилось у кошику?

7.  Назар приніс з городу 9 помідорів. 6 помідорів з'їли під час обіду. Скільки помідорів залишилось?

8.  Туристи взяли в похід 8 банок консервів. За два дні вони з'їли 5 банок. Скільки банок консервів залишилось?

9.  На лісовій галявині було 10 зайчиків. Невдовзі, злякавшись лисиці, три зайчики втекли геть. Решта зайців заховалися на галявині. Скільки зайчиків заховалося на галявині?

10.У вазі було 5 огірків і 5 помідорів. Для салату використали 4 помідори. Скільки помідорів залишилось?

11.Оксана виготовила 8 ялинкових прикрас. 5 прикрас вона принесла у школу. Скільки ялинкових прикрас залишилося в Оксани?

12.У бочці було 9 відер води. Для поливання городу використали 6 відер води. Скільки відер води залишилось у бочці?

13.У гаражі стояло 10 таксі. Три таксі виїхало. Скільки таксі залишилось у гаражі?

14.На лавці сиділо 5 дітей. Три дівчинки пішли додому. Скільки дітей залишилося на лавці?

15.У підвал веде 7 східців. Хлопчик зійшов на три східці вниз. Скільки східців йому залишилося ще подолати?

16.У глечику 10 склянок молока. За сніданком випили 7 склянок. Скільки склянок молока залишилось?

17.Черговим по класу треба помити 7 горщиків з квітами. Вони вже помили 5. Скільки горщиків залишилося ще помити?

Додаток В. Тема уроку. Задачі на знаходження суми і остачі

 

Мета уроку. Ознайомити учнів з текстовими задачами на знаходження суми й остачі, навчити їх читати і сприймати текст задачі. Домогтися, щоб кожен учень засвоїв структуру задачі: умова і запитання та основні елементи її розв'язування (умова, запитання, розв'язання, перевірка і відповідь задачі). Формувати вміння і навички дітей вибирати потрібну дію, пояснювати вибір дії при розв'язанні задач на знаходження суми й остачі.

І варіант

Задача. В Іринки було 4 листівки, а в Олі — одна. Скільки листівок було у дівчаток?

І. Вчитель читає задачу частинами.

·  В Іринки було 4 листівки. Іринко, вийди до дошки і візьми зі столу 4 листівки. Лічи їх і клади у конверт. (Іра лічить листівки і кладе їх у конверт).

·  Скільки листівок було в Іринки?

·  В Іринки було 4 листівки.

·  В Олі була одна листівка. Олю, йди до дошки і візьми зі столу одну листівку. Поклади її у конверт. (Оля бере листівку і кладе її у конверт).

·  Скільки листівок було в Олі?

·  В Олі була одна листівка.

·  В Іринки було 4 листівки, а в Олі — одна. Це умова задачі.

·  Прочитай умову задачі, Андрійку.

·  В Іринки було 4 листівки, а в Олі — одна.

·  Що прочитав Андрійко?

·  Андрійко прочитав умову задачі.

·  Скажіть хором: "Умова задачі". Три-чотири!

·  Умова задачі.

·  Про що потрібно дізнатись?

·  Скільки листівок було у дівчаток.

·  "Скільки листівок було у дівчаток?" — це запитання задачі.

·  Прочитай запитання задачі, Сергію.

·  "Скільки листівок було у дівчаток?"

·  Що прочитав Сергій?

·  Сергій прочитав запитання задачі.

·  Скажіть хором: "Запитання задачі". Три-чотири!

·  Отже, задача складається з умови і запитання.

·  "Розв'язати задачу" означає знайти відповідь на її запитання.

·  Як дізнатися, скільки листівок у дівчаток? Яку дію треба виконати – додавання чи віднімання? Подумайте: в Іринки було чотири листівки, а в Олі — одна.

·  Треба до числа 4 додати 1.

Вчитель записує на дошці, а учні — в зошитах: "4 + 1".

·  Чому виконуємо дію додавання?

·  Якщо в Іринки було 4 листівки, а в Олі — одна, то число листівок, які були у дівчаток, дорівнює сумі чисел 4 і 1. 4 плюс 1, дорівнює 5.

·  Запишемо: 4+1=5.4+1=5 — це розв'язання задачі.

·  Повторіть хором: 4+1=5 – це розв'язання задачі. (Учні повторюють).

·  Що означає число 5?

·  У дітей було 5 листівок.

·  Ми відповіли на запитання задачі — отже, ми розв'язали задачу. У дівчаток було 5 листівок — це відповідь задачі, Повторіть хором: ''Відповідь задачі". Три-чотири!

·  Відповідь задачі.

·  Процес розв'язування задач складається з таких частин: умова, запитання, розв'язання, відповідь.

II. Первинне закріплення нового матеріалу

·  З яких частин складається процес розв'язування задачі? Пригадати це нам допоможуть Петрусь, Галинка, Надійна й Олег. (Діти виходять до дошки). Петрусь виконуватиме роль умови задачі. Він назве свою роль і прочитає умову задачі. Галинка матиме іншу роль — вона прочитає запитання задачі. Надійка прочитає розв'язання задачі, а Олег— відповідь задачі. (Учні виконують свої ролі).

·  Розглянемо задачу: "В Андрія було 5 яблук. Два яблука він віддав Сергію. Скільки яблук залишилося в Андрія?"

·  Прочитай умову задачі, Ігор.

·  В Андрія було 5 яблук. Два яблука він віддав Сергію.

·  Що прочитав Ігор?

·  Ігор прочитав умову задачі.

·  Прочитай запитання задачі, Назаре.

·  "Скільки яблук залишилося в Андрія?"

·  Що прочитав Назар?

·  Назар прочитав запитання задачі.

·  Яку дію треба виконати, щоб знайти відповідь на запитання задачі?

·  Треба виконати дію віднімання.

·  Чому треба виконати дію віднімання?

·  Андрій віддав 2 яблука, їх у нього стало менше.

·  Прочитай розв'язання задачі, Наталю.

·  Від числа 5 відняти 2, буде 3.

·  Запишіть розв'язання задачі в зошит. (Запис у зошиті: 5-2 = 3).

·  Чи правильно ми розв'язали задачу?

·  Ми одержали число 3, яке менше, ніж 5. Отже, задачу ми розв'язали правильно.

·  Прочитай відповідь задачі, Маринко.

·  В Андрія залишилося 3 яблука.

·  Прочитай умову, запитання, розв'язання і відповідь задачі, Світлано.

·  Умова задачі: "В Андрія було 5 яблук. Два яблука він віддав Сергію";запитання задачі: "Скільки яблук залишилося в Андрія?"; розв'язання задачі:"Від числа 5 відняти 2, буде 3"; відповідь задачі: "В Андрія залишилося 3 яблука.".

II варіант

Задача. Горобчик знайшов спочатку 3 вишеньки, потім — ще 2 вишеньки. Скільки всього вишеньок знайшов горобчик?

— Горобчик знайшов 3 вишеньки і поклав їх у гніздечко. (Вчитель показує З вишеньки і кладе їх у гніздечко). Це ми знаємо. Потім горобчик знайшов ще дві вишеньки. (Вчитель показує 2 вишеньки, які також кладе в гніздечко). Це ми так само знаємо. Скільки всього вишень знайшов горобчик? Про це ми не знаємо. Складаємо задачу: "Горобчик знайшов спочатку 3 вишеньки, потім — ще 2 вишеньки. Скільки всього вишеньок знайшов горобчик?" Назвемо спочатку те, що ми знаємо. Ми знаємо, скільки вишень знайшов горобчик спочатку — три. (На набірному полотні виставляється картка з цифрою 3). Потім горобчик знайшов ще дві вишеньки. (На набірному полотні виставляється картка з цифрою 2). Це умова задачі. Отже, будь-яка задача складається з умови і запитання. Щоб розв'язати задачу, треба знати, яку дію потрібно виконувати — додавання чи віднімання і чому. Якщо горобчик знайшов спочатку 3 вишеньки, а потім ще дві, то число знайдених вишень дорівнює сумі чисел 3 і 2. (На набірному полотні між цифрами 3 і 2 вчитель виставляє знак "+".) Скільки буде, якщо до числа 3 додати 2?

·  Буде п'ять.

·  Запишіть у зошитах: 3+2 = 5.

·  Ми записали розв'язання задачі: до числа 3 додати 2, буде 5.

·  Прочитайте відповідь задачі.

·  Горобчик знайшов 5 вишеньок.

·  Отже, ми дали відповідь на запитання задачі. Це означає, що задачу ми розв'язали.

Первинне закріплення нового матеріалу проводиться так само, як і в першому варіанті фрагмента уроку.