Наложить отрезанный кусок на ломоть хлеба

4. Наложить отрезанный кусок на ломоть хлеба.

Результативность. Это свойство требует, чтобы в алгоритме не было ошибок. Например, рассмотрим алгоритм нахождения большего из двух заданных чисел А и В:

Из числа А вычесть число В.

Если получилось отрицательное значение, то сообщить, что число В больше.

Если получилось положительное значение, то сообщить, что число А больше.

При всей простоте и очевидности алгоритма, не каждый сразу поймет его ошибочность. Ведь если оба числа равны, то не получится никакого сообщения. Значит, надо обязательно предусмотреть это вариант, например:

Из числа А вычесть число В.

Если получилось отрицательное значение, то сообщить, что число В больше.

Если получилось положительное значение, то сообщить, что число А больше.

Если получился ноль, то сообщить, что числа равны.

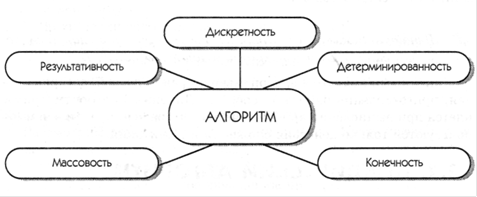
Таким образом, для любого алгоритма характерны следующие свойства: дискретность, детерминированность, конечность, массовость, результативность.

IV. Подведение итогов урока

Итак, на сегодняшнем уроке мы познакомились с понятием алгоритм, в чем состоит назначение алгоритма и каковы его основные свойства.

Материал сегодняшнего урока позволит, в дальнейшем, наиболее эффективно использовать данное нам время на изучение курса.

V. Домашнее задание

Выучить определение и свойства алгоритма

Урок на тему "Типовые конструкции алгоритма"

Цели урока:

Образовательная - систематизировать знания учащихся по теме "Алгоритмизация";

Развивающая - развивать логическое мышление у учащихся;

Воспитательная - воспитывать аккуратность, самостоятельность и культуру самостоятельной подготовки.

I. Организационный момент

Проверка готовности.

II. Сообщение темы и цели урока

- Тема сегодняшнего урока называется "типовые конструкции алгоритма".

III. Практическая часть урока

Линейный алгоритм.

Описания действий в алгоритме следуют последовательно друг за другом. Однако очередность выполнения этих действий может быть изменена, если в алгоритме предусмотрен анализ некоторого условия. Путем включения условий создаются алгоритмы с различной структурой, в которой всегда можно выделить несколько типовых конструкций: линейную, циклическую, разветвляющуюся, вспомогательную.

Знакомство с типовыми конструкциями начнем с линейного алгоритма.

Предположим, требуется составить алгоритм вычисления результата выражения:

100 + 15-40 + 20

1. Сложить числа 100 и 15.

2. Из полученной суммы вычесть 40.

3. К результату прибавить 20.

В этом примере действия выполняются в том порядке, котором записаны.

Подобные алгоритмы получили название линейных, или последовательных.

Линейный (последовательный) алгоритм - описание действий, которые выполняются однократно в заданном порядке.

Линейными являются алгоритмы отпирания дверей, заваривания чая, приготовления одного бутерброда. Линейный алгоритм применяется при вычислении арифметического выражения, если в нем используются только действия сложения и вычитания.

Циклический алгоритм.

Многие процессы в окружающем мире основаны на многократном повторении одной и той же последовательности действий. Каждый год наступают весна, лето, осень и зима.

Жизнь растений в течение

года проходит одни и те же циклы. Подсчитывая число полных поворотов минутной или часовой стрелки, человек измеряет время.

Допустим, робот обучен красить забор. Он последовательно закрашивает доску за доской.

Для робота составлен следующий алгоритм:

1. Покрасить доску.

Переместиться к следующей доске.

Перейти к действию 1.

Робот, закрасив одну доску, перейдет ко второй, затем к следующей и т.д. Робот не сможет закончить работу, так как алгоритм не предусматривает окончания работы. В приведенном примере необходимо добавить в алгоритм действие по анализу результата:

Покрасить доску.

Если есть еще доска, переместиться к следующей; перейти к действию 1.

Если доски закончились, завершить работу.

Особенно часто появляются повторяющиеся действия при вычислениях. Так действие умножения выполняется как заданное количество повторений действия сложения. Например, результат умножения 60 = 20x3 равноценен результату выполнения трехкратного сложения одного и того же числа 60 = 20+20+20.

Рассмотрим другой математический пример. Пусть требуется записать все четные двузначные числа и рассчитать их сумму, используя следующий алгоритм:

Выбрать первое четное двузначное число (10) и записать его.

Определить начальную сумму всех двузначных чисел равной 10.

Повторить п раз следующую операцию:

К предыдущему четному двузначному числу прибавить 2 и записать результат.

К предыдущей сумме двузначных чисел прибавить число, получившееся на шаге 3.1

Замечание.

В рассмотренном примере действия, пронумерованные как 3.1 и 3.2, должны повторяться 44 раза. Алгоритм, который содержит описание повторяющихся действий, принято называть циклическим.

Число повторений в циклических процессах или известно заранее, как было показано в предыдущем примере, или зависит от какого-либо условия.

Рассмотрим пример, в котором цикл задается условием. Алгоритм перевода целых десятичных двухзначных чисел в двоичную систему будет несколько сложнее, чем предыдущий:

1. Записать двузначное число.

2. Разделить исходное число на 2 и записать частное.

3. Разделить частное на 2.

4. Сравнить получившееся новое частное с числом 2.

5. Если частное оказалось больше 2, перейти к шагу 3. Если частное равно 1, то прекратить деление.

6. Записать получившийся двоичный код.

В данном примере в цикл включены три пункта (3, 4,5). Их выполнение будет продолжаться до тех пор, пока частное не станет равным 1.

Циклический алгоритм - описание действий, которые должны повторяться указанное число раз или пока не выполнено заданное условие. Перечень повторяющихся действий называется телом цикла.

Разветвляющийся алгоритм.

Вспомним сюжет из русской сказки. Царевич останавливается у развилки дороги и видит камень с надписью: "Направо пойдешь - коня потеряешь, налево пойдешь - сам пропадешь..."

Подобная ситуация, заставляющая нас принимать решение в зависимости от некоторого условия, постоянно встречается в повседневной жизни.

Если пошел дождь, то надо открыть зонт.

Если болит горло, то прогулку следует отменить.

Если прозвенел будильник, то надо вставать и идти в школу.

Если билет в кино стоит не больше десяти рублей, то купить билет и занять свое место в зале, иначе (если стоимость билета больше 10 руб) вернуться домой.

Если значение X больше нуля, то Y, равное 5 + X, также больше нуля.

Эти предложения начинаются с предположения о том, произошло или нет некоторое событие: пошел ли дождь, болит ли горло, прозвенел ли будильник и т.д. Приведенные примеры отражают суть нашего мышления. Делая какие-то предположения, мы неизбежно приходим к определенным выводам. Существует специальный раздел математики - формальная логика, которая объясняет, как выстраивать цепочку рассуждений, чтобы прийти к правильному выводу.

Логика учит правильно формулировать условие, под которым понимается предположение, начинающееся со слова "если" и заканчивающееся перед словом "то". Условие может принимать значение "истина", когда оно выполнено, или "ложь", когда оно не выполнено. От значения условия зависит наше дальнейшее поведение.

Например, в предложении "Если пошел дождь, то надо открыть зонт" условие "пошел дождь" может быть и истинным, и ложным. Поэтому в конкретной ситуации предполагается либо выполнение действия "открыть зонт", либо его пропуск - если дождя нет, то зонтик открывать незачем.

Условие - выражение, находящееся между словом "если" и словом "то" и принимающее значение "истина" или "ложь".

Порою и анализ ситуации, и сам выбор не вызывают затруднений, а иногда это сделать вовсе не просто. Приходится продумывать каждый возможный вариант и последствия принимаемого решения.

Прежде чем сделать очередной ход, шахматист анализирует позицию на много ходов вперед.

Компьютерные игры также во многом построены на анализе ситуации и выборе. Представьте: вы ведете компьютерный автомобиль. Серая лента шоссе петляет, неожиданно возникают резкие повороты. Стоит вам на мгновение замешкаться - автомобиль выносит на обочину, и вы немедленно получаете штрафные очки.

Алгоритм, в котором используется условие, получил название разветвляющегося, так как в зависимости от значения условия выбираются те или иные действия.

Если билет в кино стоит не больше десяти рублей, то купить билет и занять свое место в зале, иначе (если стоимость билета больше 10 руб) вернуться домой.

В зависимости от значения условия выполняется либо действие, указанное после слова "то" - просмотр кинофильма, либо другое действие, указанное после слова "иначе" - возвращение домой.

Разветвляющийся алгоритм - алгоритм, в котором в зависимости от условия выполняется либо одна, либо другая последовательность действии.

Итак, для того чтобы сделать выбор, надо проанализировать условие.

В общем случае схема разветвляющего алгоритма будет выглядеть так: "если условие, то..., иначе... ". Такое представление алгоритма получило название полной формы.

Вспомните кота из сказки А.С. Пушкина: "идет направо - песнь заводит, налево - сказку говорит".

В разветвляющемся алгоритме при невыполнении условия действия могут не предусматриваться. Тогда это будет неполная форма, в которой действия пропускаются: "если условие, то... ". Неполная форма разветвляющегося алгоритма напоминает поведение водителя, едущего по шоссе: если бензин на исходе, то водитель заезжает на ближайшую автозаправочную станцию.

В предложении "если выучишь урок, то получишь хорошую оценку" в зависимости от значения условия либо выполняется, либо не выполняется действие "получишь хорошую оценку".

В предложении "Если среднесуточная температура воздуха ниже 8 градусов, приступить к протапливанию помещений" в зависимости от значения условия либо выполняется, либо не выполняется действие "приступить к отапливанию помещений".

Вспомогательный алгоритм.

Допустим, вы хотите научиться жонглировать двумя или даже тремя мячами. Если внимательно приглядеться к действиям профессионального артиста и попытаться понять, как это ему удается делать, то оказывается - секрет в том, что надо научиться искусно выполнять несколько определенных движений, которым присвоим соответствующие названия:

Бросок левой - подбросить мяч левой рукой.

Бросок правой - подбросить мяч правой рукой.

Захват левой - поймать мяч правой рукой.

Захват правой - поймать мяч правой рукой.

Выполняться каждое такое действие будет по собственному алгоритму. Научившись таким действиям, вы сможете применить свое умение и в другом деле, например показывая фокусы или участвуя в соревнованиях. Благодаря тому, что подобные алгоритмы могут в дальнейшем многократно использоваться в других алгоритмах, их стали называть вспомогательными.

Алгоритм жонглирования можно записать с помощью вспомогательных алгоритмов выполнения отдельных действий в следующем виде: