Навигация
Стохастическое программирование, когда вектор неуправляемых переменных у случаен
5. Стохастическое программирование, когда вектор неуправляемых переменных у случаен.
В этом случае математическая модель задачи (1.1—1.2) будет иметь
maxMyE=My{f(x, y)}
при ограничениях
![]()
или вероятностных ограничениях
![]()
где My — математическое ожидание по у; Р{gi (х)£ b} — вероятность того, что выполняется условие gi (х)£ b.
6. Дискретное программирование, если на переменные xj наложено условие дискретности (например, целочисленности): xj — целое, j=1,2,…,n1£п.
7. Эвристическое программирование применяют для решения тех задач, в которых точный оптимум найти алгоритмическим путем невозможно из-за огромного числа вариантов. В таком случае отказываются от поиска оптимального решения и отыскивают достаточно хорошее (или удовлетворительное с точки зрения практики) решение. При этом пользуются специальными приемами — эвристиками, позволяющими существенно сократить число просматриваемых вариантов. Эвристические методы также применяют, когда оптимальное решение в принципе может быть найдено (т.е. задача алгоритмически разрешима), однако для этого требуются объемы ресурсов, значительно превышающие наличные.
По содержательной постановке выделяют следующие типичные классы задач исследования операций:
1) управления запасами,
2) распределения ресурсов,
3) ремонта и замены оборудования,
4) массового обслуживания,
5) упорядочения,
6) сетевого планирования и управления,
7) выбора маршрута,
8) комбинированные.
Из перечисленных выше методов математического программирования наиболее развитым и законченным является линейное программирование. В его рамки укладывается широкий круг задач исследования операций.
Линейное программирование
Несмотря на требование линейности целевой функции и ограничений, в рамки линейного программирования укладываются задачи распределения ресурсов, управления запасами, сетевого и календарного планирования, транспортные задачи, задачи теории расписаний и т. д.
Определение оптимального ассортимента. Имеется р видов ресурсов в количествах а1, а2, ..., аi, ..., аp и q видов изделий. Задана матрица А=||aik||, где аik характеризует нормы расхода i-го ресурса на единицу k-го изделия (k = 1, 2, ..., q).
Эффективность выпуска единицы k-го изделия характеризуется показателем сi, удовлетворяющим условию линейности.
Определить план выпуска изделий (оптимальный ассортимент), при котором суммарный показатель эффективности принимает наибольшее значение.
Количество единиц k-го изделия, выпускаемых предприятием, обозначим хk. Тогда математическая модель задачи имеет такой вид:
найти
![]() (1.3)
(1.3)
при ограничениях
![]() (1.4)
(1.4)
Кроме ограничения по ресурсам (1.3), в модель могут быть введены дополнительные ограничения на планируемый выпуск продукции xj³xj0, условия комплектности для сборки xi : хj : xk. = bi : bj : bk для всех i, j, k и т. д.
Оптимальное распределение взаимозаменяемых ресурсов. Имеются т видов взаимозаменяемых ресурсов а1, а2, ..., аi, ..., аm используемых при выполнении п различных работ в объеме b1, b2, …, bn.
Заданы числа lij, указывающие, сколько единиц j-й работы можно получить из единицы i-го ресурса, а также сij — затраты при изготовлении единицы j-го продукта из i-го ресурса.
Требуется распределить ресурсы по работам таким образом, чтобы суммарная эффективность была наибольшей (или суммарные затраты — наименьшими).
Данная задача называется общей распределительной задачей.
Количество единиц i-го ресурса, которое выделено для выполнения работ j-то вида, обозначим xij.
Математическая модель задачи такова:
найти
![]() (1.5)
(1.5)
при ограничениях
 (1.6)
(1.6)
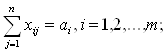 (1.7)
(1.7)
Ограничение (1.6) означает, что план всех работ должен быть выполнен полностью, а ограничение (1.7) — что ресурсы должны быть израсходованы целиком.
2. Математическая модель задачи линейного программирования (ЗЛП).
Задачу линейного программирования можно сформулировать такНайти
![]() (2.1)
(2.1)
при условиях
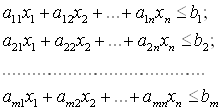 (2.2)
(2.2)
и
![]() (2.3)
(2.3)
Ограничения (2.3) называют условиями неотрицательности. В данном случае все условия имеют вид неравенств. Иногда они могут быть смешанными, т. е. неравенства и равенства.
Определение 3. Допустимым множеством решений задачи (2.1)—(2.3) называется множество R(х) всех векторов х, удовлетворяющих условиям (2.2) и (2.3).
Очевидно множество R(х) представляет собой выпуклое многогранное множество или выпуклый многогранник.
Отметим, что поскольку minF(х) эквивалентен max[-F(х)], то задачу ЛП всегда можно свести к эквивалентной задаче максимизации.
Стандартная форма задачи линейного программирования Стандартная форма задачи линейного программирования предполагает, что для всех переменных выполняется условие неотрицательности и все условия-ограничения имеют вид уравнений с неотрицательной правой частью.Допустимые базисные решения.
Пусть ограничения задачи ЛП заданы в форме уравнений, т.е. задача записана в стандартной форме и содержит m уравнений и n (n³m) переменных. Тогда все допустимые крайние точки множества допустимых решений определяются как все однозначные неотрицательные решения системы m уравнений, в которых n-m переменных равны нулю. Однозначные решения такой системы уравнений, получаемые путем приравнивания к нулю (n-m) переменных, называются базисными решениями. Если базисное решение удовлетворяет требованию неотрицательности, оно называется допустимым базисным решением. Переменные, имеющие нулевое значение называются небазисными или свободными переменными, а остальные базисными.
Основные теоремы линейного программированияВ основе методов решения задач линейного программирования лежат следующие теоремы.
Основная теорема линейного программирования, устанавливающая место нахождения оптимальных решений.
Теорема 2.1. Если целевая функция принимает максимальное значение в некоторой точке допустимого множества R, то она принимает это значение в крайней точке R (вершине выпуклого многогранника). Если целевая функция принимает максимальное значение более, чем в одной крайней точке, то она принимает это же значение в любой их выпуклой комбинации.
Из теоремы 2.1 следует, что при отыскании оптимального решения достаточно просмотреть только крайние точки допустимого множества решений R.
Теорема 2.2. Каждое допустимое базисное решение соответствует крайней точке R.
Справедлива также следующая теорема, обратная к теореме 2.2. Теорема 2.3. Если ![]() — крайняя точка допустимого множества решений R, то соответствующее решение x0 — является допустимым базисным решением системы ограничений задачи линейного программирования.
— крайняя точка допустимого множества решений R, то соответствующее решение x0 — является допустимым базисным решением системы ограничений задачи линейного программирования.
Используя результаты теорем 2.1 и 2.2, можно сделать вывод, что для отыскания оптимального решения задачи линейного программирования достаточно перебрать лишь допустимые базисные решения. Этот вывод лежит в основе многих методов решения задач линейного программирования.
Симплекс-метод.
Общая идея симплекс-метода заключается в следующем: начиная с некоторой исходной допустимой угловой точки (обычно начала координат), осуществляются последовательные переходы от одной крайней точки к другой до тех пор, пока не будет найдена точка соответствующая оптимальному решению. Решение задачи линейного программирования симплекс-методом удобно оформлять в виде симплекс-таблиц.
Алгоритм симплекс-метода состоит из следующих шагов:
Шаг 0. Используя линейную модель стандартной формы, определяют начальное допустимое базисное решение путем приравнивания к нулю n-m (небазисных) переменных. При этом если матрица системы ограничений задачи линейного программирования содержит единичную подматрицу порядка m, то это решение очевидно. Переменные, столбцы которых образуют эту единичную матрицу, являются базисными, остальные – свободными. Если же такой единичной матрицы нет, то для получения начального базисного решения вводятся искусственные переменные. Затем базисные переменные выражаются через небазисные из соответствующих ограничений и полученные выражения подставляются в целевую функцию. Если используются искусственные переменные, то применяются специальные методы (метод больших штрафов, двухэтапный метод).
Шаг 1. Из числа текущих небазисных переменных выбирается включаемая в новый базис переменная, увеличение которой обеспечивает улучшение значения целевой функции. Если такой переменной нет, вычисления прекращаются, так как полученное базисное решение оптимально. В противном случае переходят к шагу 2.
Шаг 2. Из числа переменных текущего базиса выбирается исключаемая переменная, которая должна принять нулевое решение (стать небазисной) при введении в состав базисных новой переменной.
Шаг 3. С помощью метода исключения переменных или метода Гаусса-Жордана находится новое базисное решение, соответствующее новым составам базисных и небазисных переменных и осуществляется переход к шагу 1.
Пример. Решить симплекс-методом задачу
Максимизировать z=3x1+2x2
при ограничениях x1+2x2£ 6;
2x1+x2£ 8;
-x1+x2£ 1;
x1£ 2;
x1³ 0, x2³ 0.
Решение.
Запишем задачу в стандартном видеz-3x1-2x2=0
x1+2x2+s1= 6;
2x1+x2+s2= 8;
-x1+x2+s3= 1;
x1+s4= 2,
где s1, s2, s3, s4 – дополнительные неотрицательные переменные, которые вводятся в правые части ограничений имеющих знак «£» и называются остаточными. Если задача линейного программирования является задачей оптимального распределения ограниченных ресурсов, и правые части каждого ограничения представляют запасы ресурсов, то значения остаточных переменных в любом решении показывают остаток этих ресурсов. Матрица системы ограничений содержит единичную матрицу порядка 4. Ее образуют коэффициенты при остаточных переменных, значит переменные s1, s2, s3, s4 будут базисными переменными, а x1, x2 – свободными или нулевыми.
Шаг 0. Заполняем начальную симплекс-таблицу.
| Базисные переменные | x1 | x2 | S1 | s2 | s3 | s4 | Решение В | |
| Z | -3 | -2 | 0 | 0 | 0 | 0 | 0 | Z-уравнение |
| s1 | 1 | 2 | 1 | 0 | 0 | 0 | 6 | s1-уравнение |
| s2 | 2 | 1 | 0 | 1 | 0 | 0 | 8 | s2-уравнение |
| s3 | -1 | 1 | 0 | 0 | 1 | 0 | 1 | s3-уравнение |
| s4 | 0 | 1 | 0 | 0 | 0 | 1 | 2 | s4-уравнение |
Шаг 1. Условие оптимальности или правило выбора включаемой в базис переменной. Вводимой в базис переменной в задаче максимизации (минимизации) является небазисная переменная, имеющая в Z-строке наибольший по модулю отрицательный (положительный) коэффициент. Если таких коэффициентов несколько, то выбор – произвольный и после этого переходят к шагу 2. Если таких коэффициентов нет, то решение оптимально.
Столбец симплекс-таблицы, соответствующий включаемой переменной, будем называть ведущим столбцом. В нашем случае включаем в базис переменную x1.
Шаг 2. Условие допустимости или правило выбора исключаемой из базиса переменной (одинаковое в задачах максимизации и минимизации). В качестве исключаемой из базиса переменной выбирается та базисная переменная, для которой отношение постоянной в правой части соответствующего ограничения к положительному коэффициенту ведущего столбца минимально. В случае равенства этого отношения для нескольких базисных переменных выбор делается произвольно.
Строку симплекс-таблицы, соответствующую исключаемой переменной, будем называть ведущей строкой. В нашем случае исключаем из базиса переменную s2.
Шаг 3. Вычисляем новое базисное решение и переходим к шагу 1.
Симплекс-таблица, соответствующая первой итерации:
| Базисные переменные | x1 | x2 | s1 | S2 | s3 | s4 | Решение В | |
| Z | 0 | -½ | 0 | 3/2 | 0 | 0 | 12 | Z-уравнение |
| s1 | 0 | 3/2 | 1 | - ½ | 0 | 0 | 2 | s1-уравнение |
| x1 | 1 | ½ | 0 | ½ | 0 | 0 | 4 | s2-уравнение |
| s3 | 0 | 3/2 | 0 | ½ | 1 | 0 | 5 | s3-уравнение |
| s4 | 0 | 1 | 0 | 0 | 0 | 1 | 2 | s4-уравнение |
Решение не оптимально. Включаем в базис x2 вместо s1. Вторая итерация:
| Базисные переменные | x1 | x2 | s1 | s2 | s3 | s4 | Решение В | |
| Z | 0 | 0 | 1/3 | 4/3 | 0 | 0 | 12 2/3 | Z-уравнение |
| x2 | 0 | 1 | 2/3 | -1/3 | 0 | 0 | 4/3 | s1-уравнение |
| x1 | 1 | 0 | -1/3 | 2/3 | 0 | 0 | 10/3 | s2-уравнение |
| s3 | 0 | 0 | -1 | 1 | 1 | 0 | 3 | s3-уравнение |
| s4 | 0 | 0 | -2/3 | 1/3 | 0 | 1 | 2/3 | s4-уравнение |
Решение оптимально.
Анализ решения на чувствительность.
Из оптимальной симплекс-таблицы либо непосредственно, либо при помощи простых преобразований можно получить информацию относительно
1. Оптимального решения: значения базисных переменных записаны в столбце В оптимальной симплекс-таблицы. Оптимальное значение целевой функции находится на пересечении Z-строки и столбца В оптимальной симплекс таблицы. Для рассмотренного примера: x1=10/3, x2=4/3, s1=s2=0, s3=3, s4=2/3, Zmax=12 2/3.
2. Статуса ресурсов: ресурс называется дефицитным, если в оптимальном решении он использован полностью. Остаточная переменная, соответствующая дефицитному ресурсу в оптимальном решении равна нулю. Для рассмотренного примера дефицитными будут ресурсы 1 и 2, т.к. s1=s2=0,
3. Ценности каждого ресурса: характеризуются величиной улучшения оптимального значения целевой функции, приходящегося на единицу прироста объема данного ресурса. Их еще называют теневыми ценами ресурсов или двойственными оценками. Эта информация представлена в Z-строке оптимальной симплекс-таблицы в столбцах, соответствующих остаточным переменным.
Похожие работы
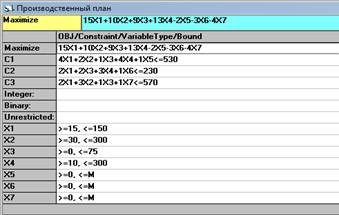
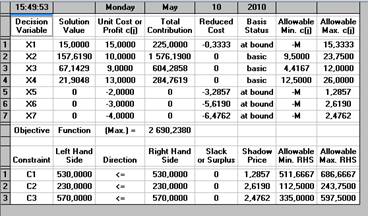
... : Ресурсы А В С D Наличие Ресурс R1 4 2 1 4 530 Ресурс R2 2 - 2 3 230 Ресурс R3 2 3 1 - 570 Прибыль 15 10 9 13 Нижн. гр. 15 30 0 10 Верхн. гр. 150 300 75 300 Построим математическую модель задачи, обозначив количество выпускаемых изделий через х1, х2, х3, х4, а целевую функцию (валовую маржинальную прибыль) — через F: F(х) = 15х1 + 10х2 + 9х3 + ...
... на одном этапе исследования, а иные – на другом. ЗАКЛЮЧЕНИЕ В процессе написания курсовой работы мною была изучена такая тема: «Аудит как метод исследования». Выяснила, что аудит входит в комплексно-комбинированные методы исследования систем управления, это указано на рис. 1, см. приложение 1. Комплексно-комбинированные методы исследования систем управления базируются на использовании ...
... ряд соображений, которые этим расчетом не были учтены. В зависимости от того, какой информацией обладают руководитель и его сотрудники, подготавливающие решения, меняются и условия принятия решений и математические методы, применяемые для выработки рекомендаций. Если известны все действующие в системе факторы, то есть отстствуют случайные воздействия, то это будет принятие решений в ...
... на операции или вскрытии. Распознавание немой формы стеноза основывается на симптомах течения болезни и состоянии легочного кровообращения и особенно легочной артерии, а также дополнительных методах исследования (рентгеноскопия, электрокардиография, катетеризация сердца и др.). 2. Форма митрального стеноза с артериальной гипертонией, присоединяющейся к митральному пороку по обычным причинам или, ...
0 комментариев