Навигация
Чувствительности оптимального решения к изменениям запасов ресурсов, вариациям коэффициентов целевой функции и интенсивности потребления ресурсов
4. Чувствительности оптимального решения к изменениям запасов ресурсов, вариациям коэффициентов целевой функции и интенсивности потребления ресурсов.
Двойственность в линейном программировании.
Любую задачу максимизации с экономической точки зрения можно рассматривать как задачу о распределении ограниченных ресурсов b1, b2,…, bn между различными потребителями, например, между некоторыми технологическими процессами, которые представляются столбцами A1, А2, ..., Аm матрицы ограничений задачи. Любое допустимое решение задачи линейного программирования х1, х2, ..., хm дает конкретное распределение, указывающее ту долю каждого из ресурсов, которая должна быть использована при осуществлении соответствующего технологического процесса.
Рассмотрим пример. Завод производит три вида продукции х1, x2 и x3, каждый из которых требует затрат времени на обработку на токарном, фрезерном и сверлильном станках. Количество машинного времени для каждого из станков ограничено. Пусть с1, c2 и c3 — прибыль от реализации единицы соответствующего вида продукции. Необходимо определить, какое количество каждого вида продукции необходимо производить в течение недели, чтобы получить максимальную прибыль.
Формально эта задача записывается так:
найти
![]() (1)
(1)
при ограничениях
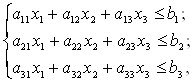 (2)
(2)
где a1j, a2j, a3j — время, необходимое для обработки единицы j-го вида продукции соответственно на токарном, фрезерном и сверлильном станках (j = 1, 2, 3); b1, b2, b3 — недельный ресурс машинного времени соответственно для токарного, фрезерного и сверлильного станков.
Обозначим y1, y2 и y3 — цену единицы времени работы на токарном, фрезерном и сверлильном станках. Тогда a1jy1 + a2jy2+ a3jy3 можно трактовать как расходы на изготовление единицы продукции вида j.
Предположим, что цены ресурсов y1, y2 и y3 выбраны так, что выполняются следующие соотношения:
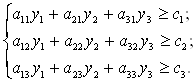 (3)
(3)
Поскольку b1, b2, b3 — использованный ресурс машинного времени для каждого из станков, то b1y1 + b2y2 + b3y3 — суммарные расходы на производство.
Требуется найти такие y1, y2 и y3, удовлетворяющие условиям (3), при которых минимизируются суммарные расходы на производство:
min g(y1, y2, y3)= b1y1 + b2y2 + b3y3, (4)
y1³ 0, y2³ 0, y3³ 0.
Такую задачу называют двойственной задачей по отношению к задаче (1), называемой прямой.
Запишем теперь прямую и двойственную задачи в общем случае. Прямая задача
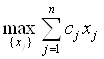 (5)
(5)
при условиях
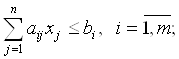 (6)
(6)
![]() . (7)
. (7)
Двойственная задача
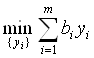 (8)
(8)
при условиях
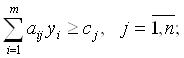 (9)
(9)
![]() . (10)
. (10)
Сопоставляя формы записи прямой и двойственной задач, можно установить между ними следующие взаимосвязи:
1) если прямая задача является задачей максимизации, то двойственная будет задачей минимизации, и наоборот;
2) коэффициенты целевой функции прямой задачи c1, c2, …, cn становятся свободными членами ограничений двойственной задачи;
3) свободные члены ограничений прямой задачи b1, b2, …, bm становятся коэффициентами целевой функции двойственной задачи;
4) матрицу ограничений двойственной задачи получают транспонированием матрицы ограничений прямой задачи;
5) если знаки всех неравенств в ограничениях прямой «£», то в двойственной задаче все ограничения будут иметь знак «³»;
6) число ограничений прямой задачи равно числу переменных двойственной задачи, а число ограничений двойственной задачи равно числу переменных прямой задачи.
Переменные y1, y2,…, ym двойственной задачи иногда называют «теневыми ценами».
Двойственную задачу выгоднее решать, чем исходную прямую, если в прямой задаче при малом количестве переменных имеется большое количество ограничений (т > n).
Связь между оптимальными решениями прямой и двойственной задач устанавливают посредством следующих теорем теории двойственности.
Теорема. Если x0 и у0 — допустимые решения прямой и двойственной задач, т. е. если Ах0 £ b и АTy0 ³ с, то
cTx0£ bTy0,
т. е. значения целевой функции прямой задачи никогда не превышают значений целевой функции двойственной задачи.
Теорема(основная теорема двойственности). Если x0 и у0 — допустимые решения прямой и двойственной задач и если cTx0=bTy0, то x0 и у0 — оптимальные решения пары двойственных задач.
Теорема. Если в оптимальном решении прямой задачи i-е ограничение выполняется как строгое неравенство, то оптимальное значение соответствующей двойственной переменной равно нулю.
Смысл этой теоремы состоит в следующем. Если некоторый ресурс bi имеется в избытке и i-е ограничение при оптимальном решении выполняется как строгое неравенство, то оно становится несущественным, и оптимальная цена соответствующего ресурса равна 0.
Теорема. Если в оптимальном решении двойственной задачи ограничение j выполняется как строгое неравенство, то оптимальное значение соответствующей переменной прямой задачи должно быть равно нулю.
Экономическая интерпретация этой теоремы: поскольку величины yj представляют собой цены соответствующих ресурсов, то 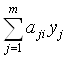 — это затраты на i-й технологический процесс, величина сi — прибыль от реализации на единицу изделия. Поэтому с экономической точки зрения теорема означает следующее: если i-й технологический процесс оказывается строго невыгодным с точки зрения оптимальных цен ресурсов уопт, то в оптимальном решении прямой задачи интенсивность использования данного технологического процесса хi должна быть равна 0.
— это затраты на i-й технологический процесс, величина сi — прибыль от реализации на единицу изделия. Поэтому с экономической точки зрения теорема означает следующее: если i-й технологический процесс оказывается строго невыгодным с точки зрения оптимальных цен ресурсов уопт, то в оптимальном решении прямой задачи интенсивность использования данного технологического процесса хi должна быть равна 0.
Таким образом, теорема выражает принцип рентабельности оптимального организованного производства.
Теорема (теорема существования). Прямая и двойственная задачи имеют оптимальные решения тогда и только тогда, когда обе они имеют допустимые решения.
Теорема (теорема двойственности). Допустимый вектор x0 оптимален тогда и только тогда, когда в двойственной задаче имеется такое допустимое решение уо, что
![]() .
.
Методы решения целочисленных ЗЛП.
Целочисленное программирование ориентировано на решение задач математического программирования, в которых все или некоторые переменные должны принимать только целочисленные значения. Задача называется полностью целочисленной, если условие целочисленности наложено на все переменные; когда это условие относится лишь к некоторым переменным, задача называется частично целочисленной. Если при этом целевая функция и функции, входящие в ограничения, линейные, то задача является задачей линейного программирования.
Методы решения задач целочисленного программирования можно классифицировать как методы отсечений (1) и комбинаторные методы (2).
Исходной задачей для методов отсечений, используемых при решении линейных целочисленных задач, является задача с ослабленными ограничениями, которая возникает в результате исключения требования целочисленности переменных. По мере введения специальных дополнительных ограничений, учитывающих требования целочисленности, многогранник допустимых решений ослабленной задачи постепенно деформируется до тех пор, пока координаты допустимого решения не станут целочисленными. Название «методы отсечений» связано с тем обстоятельством, что вводимые дополнительные ограничения отсекают (исключают) некоторые области многогранника допустимых решений, в которых отсутствуют точки с целочисленными координатами,
В основе комбинаторных методов лежит идея перебора всех допустимых целочисленных решений, разумеется, на первый план здесь выдвигается проблема разработки тестовых процедур, позволяющих непосредственно рассматривать лишь относительно небольшую часть указанных решений, а остальные допустимые решения учитывать некоторым косвенным образом. Наиболее известным комбинаторным методом является метод ветвей и границ, который также опирается на процедуру решения задач с ослабленными ограничениями. При таком подходе из рассматриваемой задачи получаются две подзадачи путем специального «разбиения» пространства допустимых решений и отбрасывания областей, не содержащих допустимых целочисленных решений.
В случае, когда целочисленные переменные являются булевыми, применяются комбинированные методы. Булевы свойства переменных существенно упрощают поиск решения.
Алгоритм метода отсечений для решения полностью целочисленной задачи.
Необходимым условием применения данного алгоритма является целочисленность всех коэффициентов и правых частей ограничений исходной задачи. Любое ограничение с рациональными коэффициентами легко приводится к требуемому виду путем умножения ограничения на наименьший общий знаменатель входящих в него коэффициентов.
Алгоритм состоит в следующем. На первом шаге решается задача с ослабленными ограничениями, не содержащая условий целочисленности переменных. Если полученное оптимальное решение оказывается целочисленным, то оно является также решением исходной задачи. В противном случае следует ввести дополнительные ограничения, порождающие (вместе с некоторыми ограничениями) новую задачу линейного программирования, решение которой оказывается целочисленным и совпадает с оптимальным решением исходной целочисленной задачи. Пусть последняя симплекс-таблица задачи с ослабленными ограничениями имеет следующий вид:
| Базисные переменные | x1 | … | xi | … | xm | w1 | … | wj | … | wn | Решение |
| Z | 0 | … | 0 | … | 0 | C1 | … | Cj | … | Cn | b0 |
| x1 | 1 | … | 0 | … | 0 | a11 | … | aj1 | … | an1 | b1 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| xi | 0 | … | 1 | … | 0 | a1i | … | aji | … | ani | bi |
| ... | … | … | … | … | … | … | … | … | … | … | … |
| xm | 0 | … | 0 | … | 1 | a1m | … | ajm | … | anm | bm |
Рассмотрим i-ую строку, которой соответствует нецелое значение базисной переменной xi, и выразим xi через небазисные переменные:
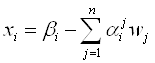 , bI – нецелое.
, bI – нецелое.
Каждую строку симплекс-таблицы, порождающую аналогичное равенство будем называть производящей строкой. Так как коэффициенты целевой функции можно считать целыми числами, переменная Z также должна быть целочисленной, и верхняя строка таблицы также может быть выбрана в качестве производящей. Пусть
bI=[bI]+fi, aji=[aji]+fij, 0<fi<1, 0£fij<1.
В качестве дополнительного ограничения вводим такое
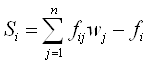 ,
,
где Si – неотрицательная дополнительная переменная, которая по определению должна принимать целые значения. Такое ограничение равенство определяет отсечение Гомори для полностью целочисленной задачи. Добавив построенное ограничение в симплекс-таблицу, получим недопустимое, но оптимальное решение. В такой ситуации следует использовать двойственный симплекс-метод для получения допустимого и оптимального решения.
Метод ветвей и границ.
На первом шаге также решается задача с ослабленными ограничениями, не содержащая условий целочисленности переменных. Но в отличие от методов отсечений этот метод может применяться как для полностью целочисленной задачи, так и для частично целочисленной. Если полученное оптимальное решение оказывается целочисленным, то оно является также решением исходной задачи. Идея метода заключается в следующем. Пусть xr целочисленная переменная, значение которой xr в оптимальном решении ослабленной задачи является дробным. Интервал
[xr]< xr<[xr]+1
не содержит допустимых целочисленных компонент решения. Поэтому допустимое целое значение xr должно удовлетворять одному из неравенств [xr]³ xr или xr³ [xr]+1. Введение этих условий в задачу с ослабленными ограничениями порождает две не связанные между собой задачи. В таком случае говорят, что исходная задача разветвляется на две подзадачи. Осуществляемый в процессе ветвления учет необходимых условий целочисленности позволяет исключить части многогранника допустимых решений, не содержащие точек с целыми координатами.
Затем каждая из подзадач решается как задача линейного программирования двойственным симплекс-методом. Если полученный оптимум оказывается допустимым для целочисленной задачи, то это решение следует зафиксировать как наилучшее. В противном случае подзадача в свою очередь должна быть разбита на две подзадачи по другой переменной и т.д.
Задача линейного программирования транспортного типа.
Постановка задачи. Пусть в m пунктах производят некоторый однородный продукт, причем объем производства в пункте i составляет Ai единиц. Допустим, что данный продукт потребляется в n пунктах потребления, а объем потребления в пункте j составляет единиц Bj. Предположим, что из каждого пункта производства i возможна транспортировка продукта в любой пункт потребления j с затратами cij. Задача состоит в определении такого плана перевозок, при котором запросы всех потребителей полностью удовлетворены, весь продукт вывезен из пунктов производства и суммарные транспортные издержки минимальны.
Математическая модель. Пусть xij – количество продукта, перевозимого из пункта i в пункт j. Найти множество переменных удовлетворяющих условиям ,
, 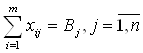 .
.
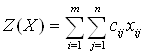 достигает минимума.
достигает минимума. Метод решения транспортной задачи [6, 7, 10].
Сети Многие задачи линейного программирования можно сформулировать и решить с помощью сетевых моделей. Специальная структура этих задач позволяет разработать эффективные алгоритмы, которые в большинстве случаев основываются на теории линейного программирования. Задача минимизации сети. Задача минимизации сети состоит в нахождении ребер, соединяющих все узлы сети и имеющих минимальную суммарную длину. Для решения задачи необходимо построить минимальное дерево-остов, применяя следующий итеративный процесс. Начать с любого узла и соединить его с ближайшим узлом сети. Соединенные узлы образуют теперь связное множество, а остальные узлы – несвязное. Далее в несвязном множестве выбрать узел, расположенный ближе всего к одному из узлов связного множества. Скорректировать соответствующим образом связное и несвязное множества, а дугу, по которой произошло присоединение запомнить. Процесс повторять до тех пор, пока все узлы не окажутся в связном множестве. Выбранные дуги образуют минимальное дерево-остов. Его длина равна сумме длин этих дуг. Задача о кратчайшем пути Задача о кратчайшем пути состоит в нахождении связанных между собой дорог на транспортной сети, которые имеют минимальную длину от исходного пункта до пункта назначения. Для решения этой задачи можно применить следующий алгоритм. Каждому узлу сети будем приписывать временные пометки равные расстоянию от начального узла до данного узла. Если оказывается, что узел принадлежит кратчайшему маршруту, то временную пометку объявляем постоянной. На первой итерации начальному узлу приписывается постоянная пометка равная нулю, а остальным узлам – временные пометки, равные длине дуги из начального узла в рассматриваемый узел, если такая дуга существует и «¥», если нет такой дуги. Затем, до тех пор пока конечный узел не получит постоянную пометку выполняются следующие две процедуры: 1) среди временных пометок выбирается минимальная и объявляется постоянной; 2) для всех временно помеченных узлов вычисляются новые временные пометки, меньшей из двух величин – старой временной пометки рассматриваемого узла и суммы постоянной пометки последнего постоянно помеченного узла и длины дуги, соединяющей последний постоянно помеченный узел с рассматриваемым узлом. Если при этом постоянную пометку получает конечный узел, то кратчайший маршрут найден. Дуги входящие в этот маршрут определяются следующим образом: если разность между постоянными пометками начального и конечного узлов данной дуги равна длине дуги, то эта дуга принадлежит кратчайшему маршрут. Задача о максимальном потоке Рассмотрим задачу о максимальном потоке между двумя выделенными узлами связной сети. Каждая дуга сети обладает пропускными способностями в обоих направлениях, которые определяют максимальное количество потока, проходящего поданной дуге. Ориентированная (односторонняя) дуга соответствует нулевой пропускной способности в запрещенном направлении. Пропускные способности cij сети можно представить в матричной форме. Для определения максимального потока из источника s в сток t используется следующий алгоритм. Шаг 1. Найти цепь, соединяющую s с t, по которой поток принимает положительное значение в направлении s®t. Если такой цепи не существует, перейти к шагу 3. В противном случае перейти к шагу 2. Шаг 2. Пусть cij- (cij+) – пропускные способности дуг цепи (s, t) в направлении s®t (t®s) и q = min{cij-}>0. Матрицу пропускных способностей (cij) изменить следующим образом: (а) вычесть q из всех cij- ; (б) прибавить q ко всем cij+ . Заменить текущую cij-матрицу на вновь полученную и перейти к шагу 1. Операция (а) дает возможность использовать остатки пропускных способностей дуг выбранной цепи в направлении s®t. Операция (б) восстанавливает исходные пропускные способности сети, поскольку уменьшение пропускной способности дуги в одном направлении можно рассматривать как увеличение ее пропускной способности в противоположном направлении. Шаг 3. Найти максимальный поток в сети. Пусть C = ççcijçç - исходная матрица пропускных способностей, и пусть C* = ççcijçç - последняя матрица, получившаяся в результате модификации исходной матрицы (шаги 1 и 2). Оптимальный поток X = ççxijçç в дугах задается как

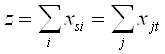 При этом z есть сумма всех положительных q, определенных на шаге 2. Таким образом, можно объяснить, почему используются положительные элементы матрицы C – C* для определения результирующего потока в направлении s® t.
При этом z есть сумма всех положительных q, определенных на шаге 2. Таким образом, можно объяснить, почему используются положительные элементы матрицы C – C* для определения результирующего потока в направлении s® t. Литература
1. Протосеня А.Г., Кулиш С.А., Азбель Е.И. и др. Математические методы планировании и управлении горным производством. Учебное пособие для вузов. - М.: Наука, 1985.
2. Филлипс Д., Гарсиа-Диас А. Методы анализа сетей. -М.: Мир,1984.
3. Пападимитриу Х., Стайглиц К. Комбинаторная оптимизация. Алгоритмы и сложность. - М.: Мир, 1985.
4. Грешилов А.А. Как принять наилучшее решение в реальных условиях. - М.: Радио и связь, 1991.
5. Попов Ю.Д. Линейное и нелинейное программирование. Учебное пособие. - Киев, 1988.
6. Зайченко Ю.П. Исследование операций. Учебное пособие для студентов вузов. - Киев: Вища школа. Головное издательство, 1979
7. Таха Х.. Введение в исследование операций: в 2-х книгах. - М.: Мир, 1985.
8. Акоф Р., Сасиени М. Основы исследования операций. - М.: Мир, 1997.
9. Акулич И.Л. Математическое программирование в примерах и задачах. - М.: Высшая школа, 1986.
10. Данко. Высшая математика в примерах и задачах.
Контрольная работа.
Контрольная работа выполняется в отдельной тетради или на листах. Контрольная работа состоит из 7 заданий, представленных в общем виде. Числовые данные к каждой задаче выдаются преподавателем и должны следовать в выполненной контрольной работе после титульного листа. Решения задач должны сопровождаться достаточными пояснениями. При решении допускается использование ПЭВМ. Контрольная работа считается выполненной, если решены все задания. Контрольная работа защищается на консультации либо в течение семестра, либо перед зачетом. К зачету допускаются только студенты, защитившие свою работу.
Задание 1
Для изготовления трех видов продукции Р1, Р2 и Р3 используют четыре вида ресурсов S1, S2, S3 и S4. Запасы ресурсов, количество каждого ресурса, затрачиваемое на изготовление единицы продукции, прибыль, получаемая от единицы продукции, приведены в таблице.
| Вид ресурса | Запас ресурса | Число единиц ресурса, затрачиваемых на изготовление единицы продукции | ||
| Р1 | Р2 | Р3 | ||
| S1 | B1 | A11 | A12 | A13 |
| S2 | B2 | A21 | A22 | A23 |
| S3 | B3 | A31 | A32 | A33 |
| S4 | B4 | A41 | A42 | A43 |
| Прибыль, получаемая от единицы продукции | C1 | C2 | C3 | |
Требуется:
a) составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной;
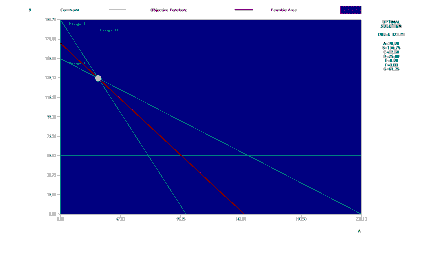
b) провести анализ на чувствительность оптимального решения к определенным изменениям исходной модели, используя оптимальную симплекс-таблицу. Для этого
1) Построить математическую модель, с подробным описанием переменных, ограничений и целевой функции.
2) Привести задачу к стандартному виду.
3) Определить начальный допустимый план.
4) Заполнить начальную симплекс-таблицу.
5) Найти оптимальный план производства симплекс-методом. (Допускается использование ПЭВМ). Решение оформить в виде симплекс-таблиц.
6) По оптимальной симплекс-таблице определить: ограничено ли пространство допустимых решений; единственно ли оптимальное решение задачи; есть ли у задачи вырожденные решения. Все ответы объяснить и обосновать.
7) Определить, какие из ресурсов являются дефицитными. Почему?
8) Определить на сколько можно увеличить запас дефицитных ресурсов, для улучшения полученного оптимального значения целевой функции.
9) Определить, на сколько можно снизить запас некоторого ресурса при сохранении полученного оптимального значения целевой функции.
10) Определить увеличение запаса какого из ресурсов наиболее выгодно.
11) Определить, в каких пределах допустимо изменение коэффициентов целевой функции.
Задание 2.
Для задачи, полученной в первом задании построить двойственную. Дать экономическую интерпретацию двойственной задачи. Решить двойственную задачу. Используя соотношения двойственности, получить оптимальное решение прямой задачи.
Задание 3.
К математической модели, полученной в задании 1 добавить условие целочисленности для всех переменных. Решить новую задачу методом отсечений.
Задание 4.
Решить транспортную задачу.
Задание 5.
Для каждой дуги (i, j) неориентированной сети указана ее длина. Построить минимальное дерево-остов.
Задание 6.
Для каждой дуги (i, j) неориентированной сети указана ее длина. Найти кратчайший маршрут из узла 1 в узел 13.
Задание 7.
Для каждой дуги (i, j) сети указана ее пропускная способность. Найти максимальный поток из источника s в сток t.
Похожие работы
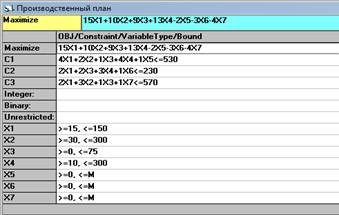
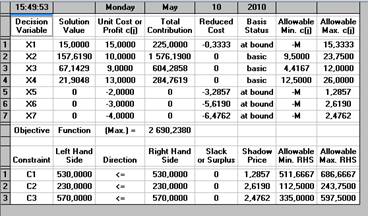
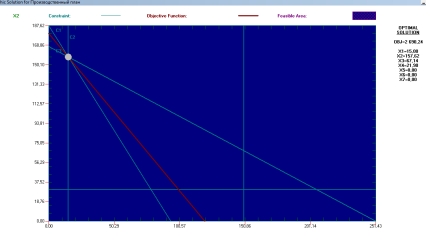
... : Ресурсы А В С D Наличие Ресурс R1 4 2 1 4 530 Ресурс R2 2 - 2 3 230 Ресурс R3 2 3 1 - 570 Прибыль 15 10 9 13 Нижн. гр. 15 30 0 10 Верхн. гр. 150 300 75 300 Построим математическую модель задачи, обозначив количество выпускаемых изделий через х1, х2, х3, х4, а целевую функцию (валовую маржинальную прибыль) — через F: F(х) = 15х1 + 10х2 + 9х3 + ...
... на одном этапе исследования, а иные – на другом. ЗАКЛЮЧЕНИЕ В процессе написания курсовой работы мною была изучена такая тема: «Аудит как метод исследования». Выяснила, что аудит входит в комплексно-комбинированные методы исследования систем управления, это указано на рис. 1, см. приложение 1. Комплексно-комбинированные методы исследования систем управления базируются на использовании ...
... ряд соображений, которые этим расчетом не были учтены. В зависимости от того, какой информацией обладают руководитель и его сотрудники, подготавливающие решения, меняются и условия принятия решений и математические методы, применяемые для выработки рекомендаций. Если известны все действующие в системе факторы, то есть отстствуют случайные воздействия, то это будет принятие решений в ...
... на операции или вскрытии. Распознавание немой формы стеноза основывается на симптомах течения болезни и состоянии легочного кровообращения и особенно легочной артерии, а также дополнительных методах исследования (рентгеноскопия, электрокардиография, катетеризация сердца и др.). 2. Форма митрального стеноза с артериальной гипертонией, присоединяющейся к митральному пороку по обычным причинам или, ...
0 комментариев