Аналіз результатів

6. Аналіз результатів

Результатом роботи програми «Adams3.exe» є таблиця значень отриманого рішення у вузлах заданої сітки, значень точного рішення й різниця між точним і отриманим рішеннями. Дану таблицю можна зберегти в текстовий файл із можливістю подальшого перегляду й редагування.

Як тестова задача була вирішена задача Коші за допомогою неявної схеми Адамса 3-го порядки на інтервалі [2,4] з початковими умовами  :

.

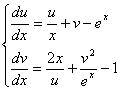Точним рішенням даної системи є функції:

Було потрібно домогтися рішення системи диференціальних рівнянь із точністю до 0.0001.

Результат рішення (вихідний файл):

Вхідні дані:

du/dx= u/x+v-e^x;

dv/dx= 2*x/u+v^2/e^x-1;

Інтервал: [2; 4]

Припустима погрішність: е=0,0001

Початкові умови:

u=4

v=7,389056098930650230

Кількість кроків сітки: 320

Крок висновку: 32

Результати:

x | u(x) | точне | різн. | v(x) | точне | різн. |

2,000 4,0000 4,0000 0,0000 7,3891 7,3891 0,0000

2,200 4,4000 4,4000 0,0000 9,0250 9,0250 0,0000

2,400 4,8000 4,8000 0,0000 11,0232 11,0232 0,0000

2,600 5,2000 5,2000 0,0000 13,4637 13,4637 0,0000

2,800 5,6000 5,6000 0,0000 16,4446 16,4446 0,0000

3,000 6,0000 6,0000 0,0000 20,0855 20,0855 0,0000

3,200 6,4000 6,4000 0,0000 24,5325 24,5325 0,0000

3,400 6,8000 6,8000 0,0000 29,9641 29,9641 0,0000

3,600 7,2000 7,2000 0,0000 36,5982 36,5982 0,0000

3,800 7,6000 7,6000 0,0000 44,7012 44,7012 0,0000

4,000 8,0000 8,0000 0,0000 54,5981 54,5982 0,0000

Час виконання: 0,015з

Як видно з отриманого результату, точність в 0.0001 досягається вже при кількості кроків, рівному 320. Час. Витрачене на розрахунок таблиці значень на заданому інтервалі становить усього 0.015 секунд, що практично не відчутно. Збільшення кроку сітки приведе до підвищення точності рішення, однак це збільшить і час роботи обчислювального процесу.

Задана точність досягається за мінімальну кількість ітерацій (1–3 ітерації).

Нижче наведений графік функцій отриманого й точного рішень:

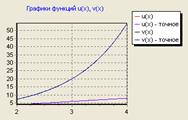
Рис. 5.1 Графік отриманого й точного рішення

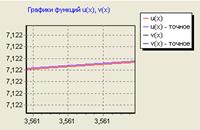
Рис. 5.2 Графік отриманого й точного рішення

Як видно з малюнків 5.1, 5.2, розбіжність кривих спостерігається тільки при досить великому збільшенні графіка.

Запропонована задача Коші була також вирішена в математичному пакеті «Mathcad 11» двома методами: методом Рунге-Кутта 5-го порядку й методом Рунге-Кутта з непостійним кроком. Реалізація рішення системи диференціальних рівнянь в «Mathcad 11» і таблиці результатів наведені нижче:

Реалізація рішення задачі Коші методом Рунге-Кутта 5-го порядку:

Таблиця 5.1 – Результати рішення задачі Коші методом Рунге-Кутта 5-го порядку.

x	u(x)	v(x)		x	u(x)	v(x)
2	4	7,3890561		3,1	6,2	22,19795
2,02	4,04	7,5383249		3,12	6,24	22,64638
2,04	4,08	7,6906092		3,14	6,28	23,10387
2,06	4,12	7,8459698		3,16	6,32	23,5706
2,08	4,16	8,0044689		3,18	6,36	24,04675
2,1	4,2	8,1661699		3,2	6,4	24,53253
2,12	4,24	8,3311375		3,22	6,44	25,02812
2,14	4,28	8,4994376		3,24	6,48	25,53372
2,16	4,32	8,6711376		3,26	6,52	26,04954
2,18	4,36	8,8463062		3,28	6,56	26,57577
2,2	4,4	9,0250135		3,3	6,6	27,11264
2,22	4,44	9,2073308		3,32	6,64	27,66035
2,24	4,48	9,3933313		3,34	6,68	28,21913
2,26	4,52	9,5830891		3,36	6,72	28,78919
2,28	4,56	9,7766804		3,38	6,76	29,37077
2,3	4,6	9,9741824		3,4	6,8	29,9641
2,32	4,64	10,175674		3,42	6,84	30,56941
2,34	4,68	10,381237		3,44	6,879999	31,18696
2,36	4,72	10,590951		3,46	6,919999	31,81698
2,38	4,76	10,804903		3,48	6,959999	32,45972
2,4	4,8	11,023176		3,5	6,999999	33,11545
2,42	4,84	11,245859		3,52	7,039999	33,78443
2,44	4,88	11,473041		3,54	7,079999	34,46692
2,46	4,92	11,704811		3,56	7,119999	35,1632
2,48	4,96	11,941264		3,58	7,159999	35,87354
2,5	4,9999999	12,182494		3,6	7,199999	36,59823
2,52	5,0399999	12,428597		3,62	7,239999	37,33757
2,54	5,0799999	12,679671		3,64	7,279999	38,09184
2,56	5,1199999	12,935817		3,66	7,319999	38,86134
2,58	5,1599999	13,197138		3,68	7,359999	39,64639
2,6	5,1999999	13,463738		3,7	7,399999	40,4473
2,62	5,2399999	13,735723		3,72	7,439999	41,26439
2,64	5,2799999	14,013204		3,74	7,479999	42,09799
2,66	5,3199999	14,296289		3,76	7,519999	42,94842
2,68	5,3599999	14,585093		3,78	7,559999	43,81604
2,7	5,3999999	14,879732		3,8	7,599999	44,70118
2,72	5,4399999	15,180322		3,82	7,639999	45,60421
2,74	5,4799999	15,486985		3,84	7,679999	46,52547
2,76	5,5199999	15,799843		3,86	7,719999	47,46535
2,78	5,5599999	16,119021		3,88	7,759999	48,42421
2,8	5,5999999	16,444647		3,9	7,799999	49,40245
2,82	5,6399999	16,776851		3,92	7,839999	50,40044
2,84	5,6799999	17,115765		3,94	7,879999	51,4186
2,86	5,7199999	17,461527		3,96	7,919999	52,45732
2,88	5,7599999	17,814273		3,98	7,959998	53,51703
2,9	5,7999998	18,174145		4	7,999998	54,59815
2,92	5,8399998	18,541287
2,94	5,8799998	18,915846
2,96	5,9199998	19,297972
2,98	5,9599998	19,687816
3	5,9999998	20,085537
3,02	6,0399998	20,491291
3,04	6,0799998	20,905243
3,06	6,1199998	21,327557
3,08	6,1599998	21,758402

Реалізація рішення задачі Коші методом Рунге-Кутта з непостійним кроком:

Таблиця 5.2 – Результати рішення задачі Коші методом Рунге-Кутта з непостійним кроком.

X	u(x)	v(x)
2	4	7,389056099
2,2	4,4	9,025013486
2,4	4,8	11,02317634
2,6	5,2	13,46373796
2,8	5,6	16,44464663
3	6	20,08553669
3,2	6,4	24,53252981
3,4	6,8	29,96409944
3,6	7,2	36,59823348
3,8	7,6	44,701183
4	8	54,59814775

Як видно з отриманих таблиць результатів, точність рішення в 0.0001 при рішенні методом Рунге-Кутта з непостійним кроком досягається всього за 10 кроків, у той час, коли для досягнення цієї ж точності при рішенні методом Рунге-Кутта 5-го порядку з постійним кроком потрібно близько 100 кроків.

Порівнюючи отримані результати з результатами роботи програми «Adams3.exe», доходимо висновку, що неявна схема Адамса третього порядку досить ефективна при чисельному рішенні задачі Коші (швидкість, висока точність рішення), однак по своїх характеристиках вона уступає більше зробленим методам, що застосовуються в різних математичних пакетах.

 

Висновок

 

Результатом виконання курсового проекту є готовий програмний продукт, що дозволяє вирішувати задачу Коші для системи диференціальних рівнянь за допомогою неявної схеми Адамса 3-го порядки, що демонструє можливості чисельного рішення поставленої задачі із заданим ступенем точності.

Готовий програмний продукт може знайти широке застосування при рішенні багатьох прикладних технічних програм, а зокрема, ефективне використання застосованої схеми Адамса 3-го порядки для рішення так званих «твердих» систем диференціальних рівнянь, для яких існує лише чисельне рішення.

Дана програма вирішує задану користувачем систему диференціальних рівнянь із зазначеною точністю за мінімальний проміжок часу. При цьому користувачеві надається можливість візуально оцінити неточність рішення, порівнюючи графіків отриманого й точного рішень.

До достоїнств програми можна віднести також зручний користувальницький інтерфейс, можливість уведення користувальницьких систем диференціальних рівнянь, а також висока стабільність роботи. Однак є й деякі недоліки. До недоліків програми можна віднести: відсутність обробки виняткових подій. Це, природно, обмежує можливості програми.

 

Література

 

1. Архангельський О.Я. Програмування в С++ Builder 6. – К., 2004

2. Каліткин М.М. Чисельні методи. – К., 2003

3. Самарський А.А., Гулін А.В. Чисельні методи. – К., 2003

4. Синіцин О.К., Навроцкий А.А. Алгоритми обчислювальної математики. – К., 2003

5. Синіцин О.К. Програмування алгоритмів у середовищі Builder C++. – К., 2003

6. Страуструп Бьерн. Язык программирования C++. – М., 2002

7. Шилд Г. Программирование на Borland C++ для профессионалов – М., 1999.

Додаток 1

 

1. Блок-схема алгоритму

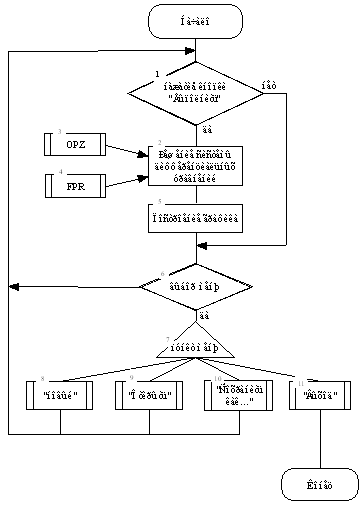
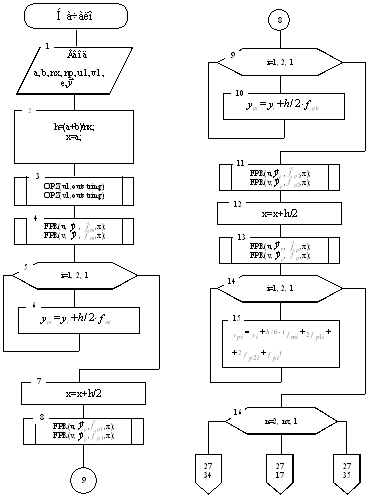
2. Блок-схема рішення задачі Коші неявною схемою Адамса 3-го порядки

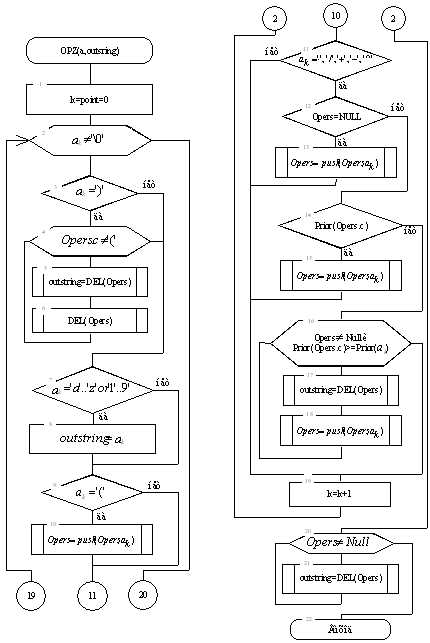
3. Блок-схема алгоритму перетворення рядка у зворотний польський запис

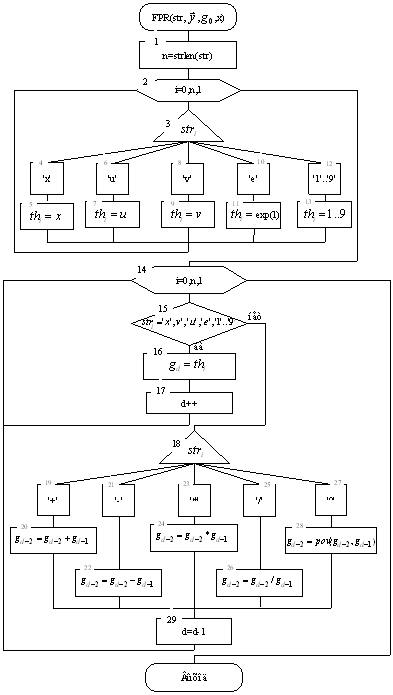
4. Блок-схема обчислення функцій