Навигация
2.3.5 Класс MatrixWindow
Конструкторы класса
MatrixWindow() - cоздает экземпляр объекта класса MatrixWindow.
Public методы
VertexMatrix GetMatrixFromDataGrid() - возвращает содержащуюся в окне матрицу.
void FillDataGrid(VertexMatrix mat) - заполняет окно матрицей mat.
void SetDefValues() - устанавливает в окне значения "Размер графа", "Размер вершин" и "Число вершин" равными по умолчанию, это 60, 10 и 0 соответственно. Граф в главном окне при этом не меняется.
void BlockGraphProp(bool block) - устанавливает возможность изменять свойства графа в окне. При block = true изменять свойства нельзя, else можно.
Private методы
void dataGridView1_ColumnAdded(object sender, DataGridViewColumnEventArgs e) - обработчик события ColumnAdded контрола, содержащего матрицу графа. Добавляет к новосозданной колонке ее порядковый номер.
void ClearDataGrid() - очищает контрол, отображающий матрицу графа. Граф при этом не изменяется.
void dataGridView1_RowsAdded(object sender, DataGridViewRowsAddedEventArgs e)- обработчик события RowsAdded контрола, отображающего матрицу графа. Нумерует новосозданные ячейки.
void dataGridView1_CellMouseDown(object sender, DataGridViewCellMouseEventArgs e) - обработчик события CellMouseDown контрола, отображающего матрицу графа. Меняет значение в кликнутой ячейке на противоположное. Значения на главной диагонали матрицы изменению не подвергаются.
Public свойства
Класс не имеет public свойств.
Private свойства
Класс не имеет private свойств.
2.3.6 Класс CliquesWindowКонструкторы класса
CliquesWindow() - cоздает экземпляр класса CliquesWindow.
Public методы
Класс не имеет public методов.
Private методы
void CliquesWindow_Load(object sender, EventArgs e) - обработчик события Load формы. Если public свойство graph не равно null вызывает процедуру поиска клик. В противном случае выводит на экран уведомление об отсутствии в графе клик.
void FindAllCliques(Graph g) - находит все клики в графе g.
Image ScaleImage(Image source, int width, int height) - изменяет масштаб изображения source на width и height. Возвращает полученное изображение.
ShowCliqueMatrix(int[] c) - отображает матрицу вершин c клики.
void SaveClique(int index) - отображает диалог сохранения клики с индексом index в файл.
void CreateReport(string filename) - создает файлы отчета обо всех найденных в графе кликах.
Public свойства
Graph graph - граф, в котором будет производиться поиск клик.
Private свойства
List<List<int>> cliques - список вершин найденных клик.
ImageList imgList - сюда заносятся изображения найденных клик.
Константы класса
int VIEW_IMAGE_WIDTH = 150 - ширина изображения клики.
int VIEW_IMAGE_HEIGHT = 150 - высота изображения клики.
3. Реализация на C# 3.1 Реализация алгоритма Брона-Кербоша
Реализация алгоритма Брона-Кербоша на С# представлена в Листинге 3.1. Представленные на нем функции являются методами класса Graph.
Листинг 3.1 – Реализация алгоритма Брона-Кербоша на С#.
public List<List<int>> FindAllCliques()
{
List<List<int>> output = new List<List<int>>();
//сюда помещаются вершины, образующие клику
List<int> M = new List<int>();
//список вершин графа
List<int> K = new List<int>();
//список "отработанных" вершин
List<int> P = new List<int>();
//вершина
int v;
Stack<int> stackV = new Stack<int>();
Stack<List<int>> stackM = new Stack<List<int>>();
Stack<List<int>> stackK = new Stack<List<int>>();
Stack<List<int>> stackP = new Stack<List<int>>();
//список несмежных с вершиной вершин
List<int> GS = new List<int>();
//заполняем список вершинами графа
for (int i = 0; i < gmatrix.Dimension; i++)
K.Add(i);
while (K.Count != 0 || M.Count != 0)
{
if (K.Count != 0)
{
v = K[0];
stackM.Push(M.GetRange(0, M.Count));
stackK.Push(K.GetRange(0, K.Count));
stackP.Push(P.GetRange(0, P.Count));
stackV.Push(v);
M.Add(v);
GS = G(v);
SubtractSet(K, GS);
SubtractSet(K, v);
SubtractSet(P, GS);
}
else
{
if (P.Count == 0) //клика найдена
output.Add(M.GetRange(0,M.Count));
M = stackM.Pop();
K = stackK.Pop();
P = stackP.Pop();
v = stackV.Pop();
SubtractSet(K, v);
P.Add(v);
}
}
return output;
}
/* вычитает вершину из множества */
void SubtractSet(List<int> set, int vert)
{
for (int i = 0; i < set.Count; i++)
{
if (set[i] == vert)
set.RemoveAt(i);
}
}
/* вычитает второе множество из первого */
void SubtractSet(List<int> set1, List<int> set2)
{
for (int i = 0; i < set1.Count; i++)
for (int j = 0; j < set2.Count; j++)
if (set1.Count != 0 && i < set1.Count)
if (set1[i] == set2[j])
set1.RemoveAt(i);
}
/* возвращает список вершин, не смежных с vert */
List<int> G(int vert)
{
List<int> ret = new List<int>();
for (int i = 0; i < gmatrix.Dimension; i++)
if (gmatrix.Get(i, vert) == 0)
ret.Add(i);
return ret;
}
Примечание: gmatrix – матрица смежности вершин, реализованная объектом класса VertexMatrix. Свойство Dimension определяет порядок матрицы (число вершин графа).
3.2 Использование нестандартных компонентов
В программе был использован элемент, не входящий в поставку .NET Framework 2.0 – DockPanel. Компонент является opensource и написан китайским разработчиком Weifen Luo (http://sourceforge.net/users/weifenluo) под лицензией MIT. Подробное описание компонента, а также исходные коды находятся на прилагаемом к курсовой компакт-диске в папке DockingWindowsComponent.
Назначение компонента
Компонент предназначен для создания "плавающих" окон, окон, способных "прилипать" к краям невидимой панели, а также быть независимыми от нее. Подобный элемент интерфейса, например, использует пакет MS Visual Studio (окна "Properties", "Solution Explorer", etc) и другие программы. Достоинства такой организации интерфейса состоит в том, что не требуемые в данный момент окна могут быть скрытыми и не занимать экранное место, а, при необходимости отображения окна, компактно располагаются по краям родительского окна, что экономит общее экранное место, или же находятся в отсоединенном ("плавающем") состоянии. Панель невидима на экране и занимает всю доступную площадь окна.
Внесенные в компонент изменения
В компонент были внесены изменения, адаптирующие его под решаемую задачу. Поскольку, как уже было сказано выше, компонент занимает всю площадь экрана, было принято решение выполнять отрисовку графа именно на нем. Первоначальный вариант панели не имел средств для рисования на ней, поэтому были внесены изменения в метод OnPaint класса DockPanel, которые находятся в файле DockPanel.cs. На листинге 3.2 показан этот метод до изменения, на листинге 3.3 – после. Также было запрещено обработка события OnPaintBackground, что позволило избежать мерцания рабочей области.
Листинг 3.2 - Первоначальное состояние метода OnPaint класса DockPanel.
protected override void OnPaint(PaintEventArgs e)
{
base.OnPaint(e);
if (DockBackColor == BackColor)
return;
Graphics g = e.Graphics;
SolidBrush bgBrush = new SolidBrush(DockBackColor);
g.FillRectangle(bgBrush, ClientRectangle);
}
Листинг 3.3 - Состояние метода OnPaint класса DockPanel после редактирования.
protected override void OnPaint(PaintEventArgs e)
{
base.OnPaint(e);
}
Как видно из листинга 3.2.2 изменение свелось к удалению запрете закраски панели собственным цветом фона. Это приведет к невозможности установки свойства BackColor компонента, но оно не используется в данном приложении.
Использование компонента в данном приложении
В данном приложении элемент DockPanel использовался для создания окна, отображающего свойства графа (класс MatrixWindow). Для этого сначала было создано окно-пустышка класса ToolWindow, наследуемое от класса DockContent. Это позволило окну ToolWindow стать "плавающим". Далее от класса ToolWindow был наследован MatrixWindow.
3.3 Реализация алгоритма удаления ребра графа мышьюЗадача: удалить ребро графа, лежащее под курсором мыши (Рис. 3.2).
Рисунок 3.2 - Мышь находится рядом с ребром графа, который требуется удалить.
Решение:
Поскольку определять пересечение курсора мыши с линией не удобно, так как при тонкой линии требуется точное позиционирование мыши, по двум точкам строятся два треугольника, которые вместе образуют прямоугольник, который делит пополам ребро графа (рисунок 3.3).
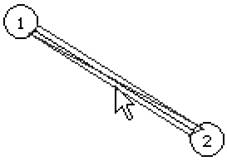
Рисунок 3.3 - Прямоугольник, образованный двумя треугольниками, делит пополам ребро графа. Координаты мыши принадлежат одному из треугольников.
Так задача сводится к одной из классических задач аналитической геометрии – определение принадлежности точки треугольнику.
Рассмотрим алгоритм определения принадлежности точки к одному треугольнику. Для начала необходимо узнать, к какой области принадлежит точка (Рис. 3.4).
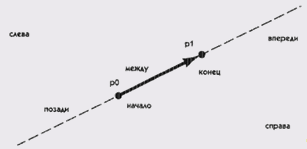
Рисунок 3.4. Области, в которых может лежать точка относительно линии.
Этим в классе Graph занимается частный метод pointClassify(Point source, Point dest), который возвращает один из элементов перечисления PointPlace, которое определяет область нахождения точки.
Перечисление PointPlace:
enum PointPlace : int
{
LEFT = 0,
RIGHT = 1,
BEYOND = 3,
BEHIND = 4,
BETWEEN = 5,
ORIGIN = 6,
DESTINATION = 7,
}
Листинг 3.4 – Метод pointClassify класса Graph.
PointPlace pointClassify(PointF point, PointF origin, PointF dest)
{
PointF a = dest;
a.X -= origin.X;
a.Y -= origin.Y;
PointF b = point;
b.X -= origin.X;
b.Y -= origin.Y;
double sa = a.X * b.Y - b.X * a.Y;
if (sa > 0.0)
return PointPlace.LEFT;
if (sa < 0.0)
return PointPlace.RIGHT;
if ((a.X * b.X < 0.0) || (a.Y * b.Y < 0.0))
return PointPlace.BEHIND;
if (Math.Sqrt(a.X * a.X + a.Y * a.Y) < Math.Sqrt(b.X * b.X + b.Y * b.Y))
return PointPlace.BEYOND;
if (point == origin)
return PointPlace.ORIGIN;
if (point == dest)
return PointPlace.DESTINATION;
return PointPlace.BETWEEN;
}
Далее достаточно определить лежит ли точка в области, образованной ребрами треугольника. Эту задачу выполняет метод pointInTriangle, который принимает координаты треугольников и точку, принадлежность треугольникам которой следует проверить. Метод возвращает true, если точка принадлежит треугольнику и false в противном случае.
Листинг 3.5 – Метод pointInTriangle класса Graph.
bool pointInTriangle(PointF p, PointF a, PointF b, PointF c)
{
return ((pointClassify(p, a, b) != PointPlace.LEFT) &&
(pointClassify(p, b, c) != PointPlace.LEFT) &&
(pointClassify(p, c, a) != PointPlace.LEFT));
}
Более подробное описание алгоритмов можно найти по следующим ссылкам:
1. http://algolist.manual.ru/maths/geom/belong/poly2d.php
2. http://algolist.manual.ru/maths/geom/datastruct.php
3.4 Тестирование реализации алгоритма Брон-КербошаТестирование алгоритма производилось:
– на пустом графе
– на графе с единственной вершиной
– не графе с тремя не соединенными ребрами вершинами
– на графе из двух вершин, соединенных ребром
– на сложном графе
Стратегия тестирования
Сперва, с помощью определения понятия "клика", были найдены клики данного графа, после чего результаты сравнивались с результатом работы программы.
Похожие работы
... и алгоритмы на основе методов целочисленного линейного программирования. К приближенный алгоритмам раскраски относятся алгоритмы, основанные на упорядочивании множества вершин графов , последовательном удалении из графа вершин, имеющих максимальную степень и на анализе подмножеств смежности вершин. 2.1 Точные алгоритмы Алгоритм, использующий метод Магу - Вейссмана 1. Для графа G (Х,U) ...
... Gg:=Qp*A[i]; end Закончим трассировку примера. 2 [5] [2] [] 1 [5] [1,2,3] [] Выход в основную программу. Мы нашли все максимальные независимые множества. 3. Доминирующие множества Для графа G=(V, E) доминирующее множество вершин есть множество вершин SÌV, такое, что для каждой вершины j, не входящей в S, существует ребро, идущее из некоторой вершины ...
0 комментариев