Алгоритм раскраски графа (точный)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Кафедра САПР

Пояснительная записка

к курсовому проекту по дисциплине

“Дискретная математика”

На тему: “Алгоритм раскраски графа (точный)"

Выполнил: студентка гр. 06ВА-1

Молоткова Е.

Принял: к.т.н., доцент Валько А.Ф.

Пенза 2007г.

СОДЕРЖАНИЕ

Аннотация

1. Теоретическая часть

2. Алгоритм, использующий метод Магу - Вейссмана

2.2 Разработанный алгоритм

3. Описание программы

3.1 Общие сведения

3.2 Вызов и загрузка

3.3 Функциональное назначение

3.4 Описание логической структуры программы

3.5 Инструкция пользователю

3.6 Решение контрольных примеров

Заключение

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

ПРИЛОЖЕНИЕ

Аннотация

В настоящей пояснительной записке приведено описание алгоритма раскраски графа (точный). Изложены вопросы проектирования структуры программы и данных. Разработаны схемы алгоритмов решения задачи. Разработана и отлажена программа, реализующая представленные алгоритмы на языке Visual C. Представлены результаты решения контрольных примеров, выполненные с помощью разработанной программы на ПК Intel core 2 Duo.

Пояснительная записка содержит 34 страницы, 5 рисунков, 4 использованных источника, приложения.

1. Теоретическая часть

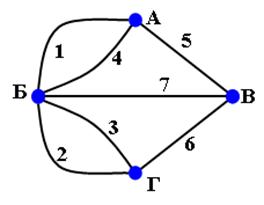
Графом,в общем случае, называются два множества, находящиеся между собой в некотором отношении: G=(V,Е), где V – множество вершин, Е – множество связей между ними . Вершины графа изображаются точками, а связи между ними – линиями произвольной конфигурации.

Связь неупорядоченной пары вершин называется ребром, упорядоченной- дугой. Граф, у которого все вершины соединены дугами называется ориентированным. Граф, у которого все вершины соединены ребрами называется неориентированным, если в графе присутствуют и ребра и дуги, то такой граф называется смешанным.

Две вершины называются смежными, если они определяют дугу (ребро), и две дуги называются смежными, если они имеют общую вершину. Вершина инцидентна дуге (ребру), если она является началом или концом этой дуги(ребра). Аналогично, дуга (ребро) инцидентна вершине, если она входит или выходит из этой вершины. Число дуг(ребер), инцидентных некоторой вершине, называют локальной степенью данной вершины.

Граф, в котором любая пара вершин соединена ребром называется полным. Полный граф обычно обозначают через К_n (n – число вершин в графе).

Число ребер полного графа m=n*(n-1)/2. Полный подграф G`=(X`,U`)графа G=(Х,U), X`εX называется максимальным полным подграфом (МПП) или кликой , если этот подграф не содержится в большем (по числу вершин) полном подграфе.

Максимальный полный подграф, содержащий наибольшее число вершин из всех МПП графа называется наибольшим полным подграфом (НПП). Число вершин наибольшего полного подграфа называется плотностью графа – φ(G). Если две любые вершины подмножества X` графа G(Х,U), где X`εX не смежны, то подмножество X` называется внутренне устойчивым.

Подмножество ψ_i X графа G(Х,U) называется максимальным внутренне устойчивым подмножеством (МВУП), или независимым подмножеством (НП), если добавление к нему любой вершины x_jεХ делает его не внутренне устойчивым. Подмножество Y_i будет определяться как х_jεψ_i (Гх_j uψ_i =)

МВУП различаются по числу входящих в них элементов. МВУП, содержащее наибольшее число элементов (вершин), называют наибольшим (предельным). Мощность НВУП (число вершин наибольшего ВУП) называется числом внутренней устойчивости

h (G) = |mах ψ_i |, где ψ_iεψ, ψ-семейство всех МВУП.

Число внутренней устойчивости называет также неплотностью графа.

Задачи определения наибольших полных подграфов и НВУП являются дополнительными друг к другу. Наибольшему полному подгра­фу графа G=(Х,U) соответствует наибольшее ВУП в графе G=(Х,U), где U_полн\U, U_полн – множество ребер полного графа, построенного на n вершинах. Аналогичные рассуждения могут быть сделаны и для максимальных НП и МВУП.

Все эти задачи относятся к так называемым NP полным задачам, временная сложность которых экспоненциальна относительно входа (числа вершин или ребер графа).

Согласно классификации всех задач теории графов по их сложности, приведенной в основополагающей работе Э. Рейнгольда и других, задачи определения МВУП и МПП (нахождение клик) графа по сложности относятся к четвертому классу задач, для которых не существует и не может существовать точного полиноминального алгоритма, так как задачи этого класса обязательно экспоненциальные относительно входа. Задачи определения НПП и МВУП (наибольшей клики) относятся к третьему классу, для которого открытие полиноминального алгоритма возможно.