Тестирование на пустом графе

1.  Тестирование на пустом графе.

Теоретические расчеты: поскольку граф пуст (множество его вершин есть пустое множество) клик в нем нет.

Практический результат: клик в графе не найдено, получено соответствующее уведомление (рисунок 3.5).

Рисунок 3.5. Сообщение об отсутствии клик в графе.

Результат: теоретические и практические расчеты сходятся – на данном наборе алгоритм работает верно.

2. Тестирование на графе с единственной вершиной.

Теоретические расчеты: граф не содержит клик - подмножество его вершин, такое, что между каждой парой вершин этого подмножества существует ребро и, кроме того, это подмножество не принадлежит никакому большому подмножеству с тем же свойством.

Практический результат: клик в графе не найдено, получено соответствующее уведомление (рисунок 3.5).

Результат: теоретические и практические расчеты сходятся – на данном наборе алгоритм работает верно.

3.Тестирование на графе с тремя не соединенными ребрами вершинами.

Теоретические расчеты: аналогичны расчетом в пункте 2.

Практический результат: клик в графе не найдено, получено соответствующее уведомление (рисунок 3.5).

Результат: теоретические и практические расчеты сходятся – на данном наборе алгоритм работает верно.

4.Тестирование на графе из двух вершин, соединенных ребром.

Теоретические расчеты: граф удовлетворяет понятию "клика".

Практические результаты: найдена одна клика, представляющая собой данный граф. Результат: теоретические и практические расчеты сходятся – на данном наборе алгоритм работает верно.

Тестирование на сложном графе.

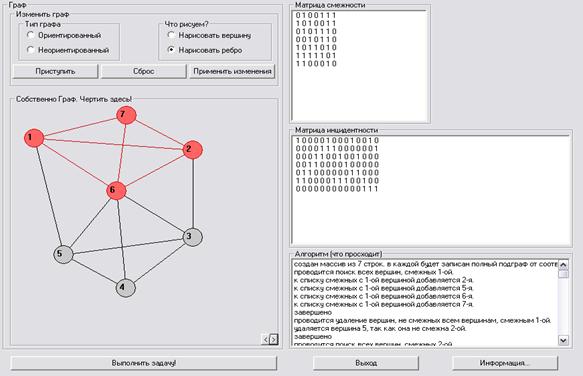
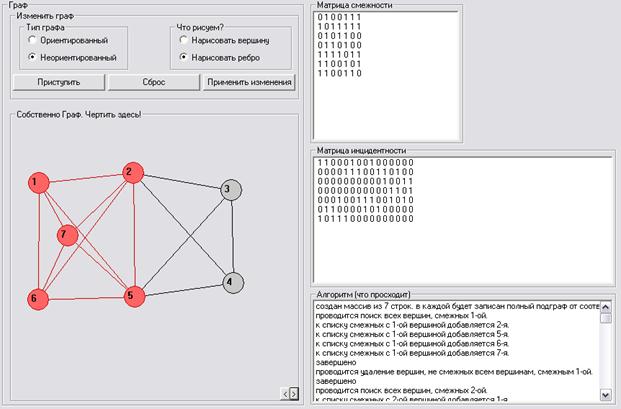
В программе был создан граф, представленный на рисунке 3.6.

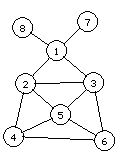
Рисунок 3.6. Сложный граф, используемый в тесте.

Матрица смежности графа:

100011

10111000

11001100

01001100

01110100

00111000

10000000

10000000

Теоретические расчеты: алгоритмом должны быть найдены следующие клики: {1,2,3},{1,7},{1,8},{2,3,5},{2,4,5},{3,5,6},{4,5,6}.Практические результаты: программой был сгенерирован отчет, представленный на листинге 3.6.

Листинг 3.6. Отчет, сгенерированный программой.

Graph untitled.g

Vertices count: 8

Matrix:

100011

111000

001100

001100

110100

111000

000000

000000

Cliques count: 7

Clique 1

Vertices: 1 2 3

Matrix:

1

1

0

Clique 2

Vertices: 1 7

Matrix:

Clique 3

Vertices: 1 8

Matrix:

Clique 4

Vertices: 2 3 5

Matrix:

1

1

0

Clique 5

Vertices: 2 4 5

Matrix:

1

1

0

Clique 6

Vertices: 3 5 6

Matrix:

1

1

0

Clique 7

Vertices: 4 5 6

Matrix:

1

1

0

Результат: алгоритм работает верно.

  3.5 Системные требования

Требования к аппаратному обеспечению:

Процессор с тактовой частотой 1000 МГц.

Не менее 256 Мб оперативной памяти.

Монитор с разрешением 1024 x 768.

Клавиатура, мышь.

Требования к программному обеспечению:

OS Windows Xp/Vista/7

NET Framework 2.0

 
Заключение

На языке программирования C# была выполнена реализация алгоритма Брона-Кербоша по поиску клик в неориентированном графе. Также были реализованы средства создания и редактирования неориентированного графа, а также поиска и отображения его клик и создания отчета о найденных кликах. Также были получены следующие навыки:

–  Умение применять и модифицировать opensource-компоненты.

–  Навык работы с динамическими структурами данных.

–  Навык организации печати документов средствами .NET Framework.

Список использованной литературы и источников

1.  Bron C., Kerbosh J. (1973), Algorithm 457 — Finding all cliques of an undirected graph, Comm. of ACM, 16, p. 575—577

2.  Cazals, F.; Karande, C. (2008), "A note on the problem of reporting maximal cliques", Theoretical Computer Science 407 (1): 564–568,doi:10.1016/j.tcs.2008.05.010

3.  Graph Drawing: Algorithms for the Visualization of Graphs.

4.  Drawing Graphs : Methods and Models (Lecture Notes in Computer Science).

5.  http://sourceforge.net/projects/dockpanelsuite/

6.  http://nzeemin.livejournal.com/184415.html

7.  http://algolist.manual.ru/maths/geom/datastruct.php

8.  http://algolist.manual.ru/maths/geom/belong/poly2d.php

Приложение

Руководство пользователя

Описание интерфейса

На рисунке 1 представлено главное окно приложения. Цифрами отмечены:

1.  Рабочая область приложения.

2.  Созданный на рабочей области граф.

3.  Главное меню приложения.

4.  Панель инструментов приложения.

5.  Окно, отображающее матрицу смежности и параметры графа.

6.  Матрица смежности графа.

7.  Параметры графа.

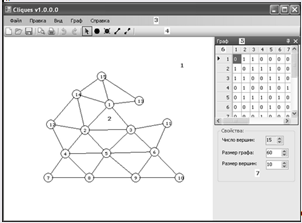
Рисунок 1. Главное окно приложения.

Панель инструментов программы (Рис. 2):

1.  Кнопка создание нового документа.

2.  Открытие нового документа.

3.  Сохранение изменений в документе.

4.  Предварительный просмотр документа перед печатью.

5.  Кнопка печати документа.

6.  Отменить сделанное изменение (если таковое имело быть).

7.  Отменить отмену изменение (если таковое имело быть).

8.  Инструмент "Курсор".

9.  Инструмент "Добавить вершину".

10.  Инструмент "Удалить вершину".

11.  Инструмент "Добавить ребро".

12.  Инструмент "Удалить ребро".

Рисунок 2. Панель инструментов приложения.

Инструменты:

Инструмент "Курсор" необходим для изменения координат вершин графа. Для изменения координат вершины графа достаточно навести курсор на вершину, и зажать левую кнопку мыши. Теперь, пока кнопка не была опущена, координаты вершины будут меняться в соответствии с изменениями координат мыши. Для окончания перемещения графа необходимо отпустить кнопку мыши.

Инструмент "Добавить вершину" создает новую вершину в кликнутой рабочей области. Строка и столбец этой вершины в матрице заполняются нулями.

Инструмент "Удалить вершину" удаляет из графа вершину, по которой кликнули мышью.

Инструмент "Добавить ребро" создает новое ребро графа. Для этого нужно выделить одну из вершин, которой будет принадлежать ребро, мышью и, не отпуская левую кнопку, перетащить курсор на вторую вершину.

Инструмент "Удалить ребро" удаляет ребро графа, по которому кликнули мышью.

На рисунке 3 представлено окно "Граф", задачей которого ставится отображение матрицы и параметров графа. Оно позволяет добавлять и удалять вершины, а также устанавливать или удалять ребра графа. Окно является "плавающим" (Docking), что означает, что оно способно "прилипать" к краям главного окна, а также быть полностью независимым от него. Отобразить или скрыть это окно возможно при помощи функции меню Вид - > Окно свойств.

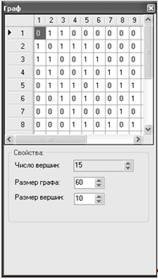
Рисунок 3. Докинговое окно "Граф".

На рисунке 4 представлено окно "Клики графа", задачей которого ставится поиск и отображения всех клик графа, а также сохранение отдельных клик в графический, текстовый или графовый (*.g) файл, а также создание отчета обо всех найденных кликах. Доступ к окну можно получить из меня Граф -> Операции -> Поиск клик. Следует отметить, что если граф не создан или в нем отсутствуют клики, пользователь не получит доступ к окну, получив соответствующее уведомление.

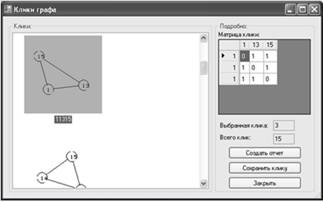
Рисунок 4. Окно "Клики графа".

Назначение кнопок:

Кнопка "Создать отчет" создает отчет обо всех найденных кликах в текстовом формате.

Кнопка "Сохранить клику" сохраняет выбранную клику в одном из выбранных форматах (граф, матрица, графический файл).

Кнопка "Закрыть" закрывает окно и дает доступ к главному окну приложения.

Формат отчета о найденных кликах

Graph: имя_файла_графа

Vertices: число_вершин_в_графе

Matrix:Матрица графа

Cliques count: число_клик_в_графе

Clique номер_клики

Vertices: вершины,_образующие_клику

Matrix:Матрица клики.

Кликовый блок содержит число записей, равное числу клик в графе.

Работа с программой

Запуск программы

Запуск программы осуществляется стандартным способом запуска приложений Windows.

Создание графа

Граф создается либо путем манипуляции инструментами, либо из файла матрицы или графа. Для того чтоб создать граф из файла матрицы или графа, следует кликнуть по кнопке "Открыть" панели инструментов, либо щелкнуть по пункту меню Файл - > Открыть. В появившимся диалоговом окне открытия файла выбрать нужный и нажать кнопку "Открыть"

Редактирование графа

Редактирование графа может осуществляться как инструментами, так и при помощи окна "Граф". Данное окно позволят задавать связи между вершинами, а также изменять размер графа.

Отмена сделанных изменений

Для отмены произведенных в графе изменений следует нажать кнопку "Отменить" на панели инструментов, либо воспользоваться горячей клавишей Ctrl+Z. Также эта функция доступна из меню "Правка", пункт "Отменить".

Отмена отмены сделанных изменений

Для отмены отмены произведенных в графе изменений следует нажать кнопку "Повторить" на панели инструментов, либо воспользоваться горячей клавишей Ctrl+Y. Также эта функция доступна из меню "Правка", пункт "Повторить"

Поиск клик в графе

Для вызова окна поиска клик следует обратиться к пункту меню "Граф" - > "Операции с графом" - > "Поиск клик".

Если в графе были найдены клики, появится окно "Клики графа", содержащее все изображения клик, а также их матрицы смежности. В противном случае будет показано уведомление об отсутствии в графе клик.

Создание отчета о найденных кликах

Для создания отчета о найденных кликах следует вызвать окно "Клики графа" (Меню "Граф"->"Операции с графом" ->"Поиск клик"). Если в графе были найдены клики, нажать кнопку "Создать отчет", тем самым, вызвав стандартное диалоговое окно сохранения файла. В нем следует ввести имя создаваемого отчета и нажать на кнопку "Сохранить". Программой будет сгенерирован отчет в текстовом формате, содержащий информацию об исходном графе и всех содержащихся в нем кликах. Также будет создан графический файл в формате png, содержащий все изображения найденных клик.

Сохранение созданного графа

Для сохранения созданного графа следует нажать на кнопку "Сохранить" панели инструментов или воспользоваться горячей клавишей Ctrl+S. Эти действия приведут к вызову стандартного диалога сохранения файла Windows.

Выход из программы

Выход из программы осуществляется по горячей клавише Alt+F4, либо при помощи стандартных методов закрытия оконных приложений Windows. Также завершить работу с программой можно при помощи меню "Файл" -> "Выход". Следует отметить, что если, во время работы с программой, создавался новый или модифицировался уже существующий граф, будет вызвано диалоговое окно с предложением сохранить выполненные изменения.